Résumé des points de connaissance sur les triangles congruents et les graphiques associés pour les élèves du secondaire de deuxième année publié par People's Education Press

Résumé des points de connaissance des triangles congruents et des connaissances graphiques associées de la version mathématique de deuxième année de People's Education Press

Chapitre 11

Révision des triangles congruents

Les triangles congrus sont définis comme deux triangles pouvant se chevaucher complètement. Les triangles congrus ont exactement la même forme et la même taille, quelle que soit leur position. Par translation, retournement et rotation, un triangle peut être transformé en un autre triangle congruent.

Les triangles congrus ont les propriétés suivantes : les côtés correspondants sont égaux, les angles correspondants sont égaux et ils ne changent pas en raison des changements de position.

Compréhension : Pour les triangles congrus, les côtés longs correspondent aux côtés longs, et les côtés courts correspondent aux côtés courts. Le plus grand angle correspond au plus grand angle et le plus petit angle correspond au plus petit angle. Les côtés opposés des angles correspondants sont congrus et les angles opposés des côtés correspondants sont congrus. Par conséquent, les triangles congrus ont des périmètres et des aires égales.

Il existe trois façons de déterminer des triangles congruents : côté-côté, angle-côté et côté-angle-côté. Parmi eux, side-side-side (SSS) signifie que lorsque les trois côtés de deux triangles sont égaux, les deux triangles sont congrus. Cette méthode de détermination peut être abrégée en « SSS ». De plus, pour les triangles congrus, les médianes, bissectrices et altitudes correspondantes sur les côtés correspondants sont également égales. Autrement dit, si deux triangles sont congrus, alors les médianes, les bissectrices et les altitudes correspondantes sur leurs côtés correspondants sont également congruentes. Pour résumer,

Angle Côté : Deux côtés et leur angle inclus correspondent à deux triangles congrus (SAS). Angles et côtés : Deux triangles sont congrus (ASA) si leurs angles et leurs côtés inclus sont égaux.

Côté angulaire : Deux triangles dont les deux angles et le côté opposé de l'un des angles sont égaux sont congrus (peut être abrégé en "AAS") Côté angle, hypoténuse, côté droit

Deux triangles rectangles avec des côtés rectangles égaux peuvent être prouvés par la condition que l'hypoténuse et les côtés rectangles sont égaux, ce qui est la condition de congruence "HL". L'idée de base pour prouver que deux triangles sont congrus est la suivante.

) : Deux côtés connus (1) : Deux côtés connus) : Deux côtés connus --- trouver le troisième côté (SSS), trouver l'angle inclus (SAS), trouver s'il existe un angle droit (HL), trouver un autre angle adjacent ici (ASA)

Trouvez ici un autre angle adjacent. Côté connu et son angle adjacent (2) : Côté connu et un angle connu - Côté connu et son angle opposé est un angle droit. à part

On sait que l'angle est un angle droit, trouvez un côté (HL) Trouvez l'autre côté de cet angle (SAS) Trouvez l'autre côté de cet angle Trouvez l'angle opposé ici (AAS) Trouvez un angle (AAS) Trouvez un angle

Trouver le côté inclus entre deux angles (ASA) Trouver le côté inclus entre deux angles (3) : Deux angles connus Deux angles connus - Deux angles connus Trouver n'importe quel côté en dehors du côté inclus (AAS) Trouver n'importe quel côté en dehors du côté inclus Côté

2. Bissectrice de l'angle : Un rayon est tiré du sommet d'un angle pour diviser l'angle en deux angles égaux. Ce rayon est appelé la bissectrice de l'angle.

1. Propriété : La distance entre le point de la bissectrice de l'angle et les deux côtés de l'angle est égale. 2. Jugement : Le point ayant la même distance de l'intérieur de l'angle aux deux côtés de l'angle est sur le. bissectrice de l'angle. Lorsque vous apprenez les triangles congruents, vous devez faire attention aux problèmes suivants :

3. Lorsque vous apprenez les triangles congruents, vous devez faire attention aux problèmes suivants : (1) Distinguer correctement les différentes significations de « côtés correspondants » et « côtés opposés » et « angles correspondants » et « angles opposés » (2

;

signifie que lorsque deux triangles sont congrus, les lettres indiquant les sommets correspondants doivent être écrites aux positions correspondantes (3) Deux triangles qui « ont trois angles égaux » ou « ont deux côtés et les angles diagonaux de l'un d'eux ; sont égaux » ne sont pas Ils doivent être congruents ; (4) Faites toujours attention aux conditions implicites dans les graphiques, telles que « angles communs », « côtés communs » et « angles opposés » (5) Coupez le long et remplissez le court pour prouver que les triangles sont congrus.

Quelles sont les méthodes pour prouver des triangles congruents au collège

Pour vérifier deux triangles congrus, utilisez généralement le côté côté (SSS), le côté angle latéral (SAS), l'angle côté angle (ASA), l'angle côté angle (AAS) et l'hypoténuse d'un triangle rectangle, le côté angle droit (HL) 5 méthode pour déterminer.

Méthode de jugement :

1. SSS (Side-Side-Side) : Un triangle avec trois côtés égaux est un triangle congru.

2. SAS (Side-Angle-Side) : Un triangle dont les deux côtés et leurs angles inclus sont égaux est un triangle congru.

3. ASA (Angle-Side-Angle) : Les deux angles et leurs côtés inclus sont congrus aux triangles égaux correspondants.

4. AAS (Angle-Angle-Side) : Deux angles et le côté opposé d'un angle correspondent à des triangles égaux et congrus.

5. RHS (Right angle-Hypotenuse-Side) (également connu sous le nom de théorème HL (hypoténuse, côté rectangle)) : Dans une paire de triangles rectangles, l'hypoténuse et l'autre côté rectangle sont égaux. (Sa preuve utilise le principe SSS)

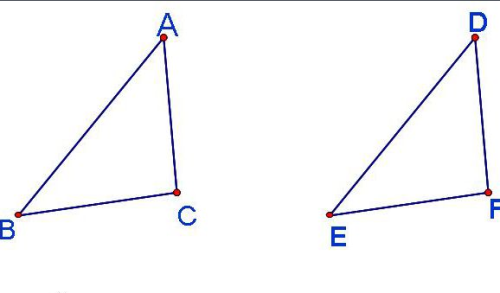
Informations détaillées :

1. Propriétés des triangles congrus

1. Les angles correspondants des triangles congrus sont égaux.

2. Les côtés correspondants des triangles congrus sont égaux.

3. Les sommets qui peuvent se chevaucher complètement sont appelés sommets correspondants.

4. Les hauteurs des côtés correspondants des triangles congrus sont égales.

5. Les bissectrices des angles correspondants des triangles congrus sont égales.

6. Les lignes médianes des côtés correspondants des triangles congrus sont égales.

7. L’aire et le périmètre des triangles congrus sont égaux.

8. Les valeurs des fonctions trigonométriques des angles correspondants des triangles congrus sont égales.

2. Inférence

1. SSS (Côté-Côté-Côté) :

Si les longueurs des trois côtés de chaque triangle sont égales, les deux triangles sont des triangles congrus.

2. SAS (Côté-Angle-Côté) (côté, angle, côté) :

Si les longueurs des deux côtés de chaque triangle sont égales et que les angles entre les deux côtés (c'est-à-dire les angles formés par les deux côtés) sont égaux, les deux triangles sont des triangles congrus.

3.ASA (Angle-Côté-Angle) :

Si deux angles de chaque triangle sont égaux, et si les côtés inclus (c'est-à-dire les côtés communs) des deux angles sont égaux, les deux triangles sont des triangles congrus.

4. AAS (Angle-Angle-Côté) :

Si deux angles de chaque triangle sont égaux, et si les côtés opposés de l'un des angles (le côté du triangle autre que les deux côtés qui composent l'angle) ou les côtés adjacents (c'est-à-dire le côté qui constitue le angle) sont égaux, les deux triangles sont des triangles congrus.

5. Théorème HL (hypoténuse-jambe) (hypoténuse, côté rectangle) :

Dans un triangle rectangle, une hypoténuse et un côté droit sont égaux, et les deux triangles sont des triangles congrus.

Source de référence : Encyclopédie Sogou-Triangles congruents

Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!