Explication détaillée de l'opération de suppression d'arbre B : Illustration détaillée de l'opération de suppression d'arbre B à l'aide de Python

L'opération de suppression de l'arbre B doit prendre en compte l'emplacement et l'équilibre des nœuds, et un sous-débordement est susceptible de se produire. Un dépassement de capacité se produit lorsqu'un nœud contient moins que le nombre minimum de nœuds enfants qu'il devrait contenir.

Les images et le texte montrent le principe de suppression de l'arbre B

sans affecter la balance.

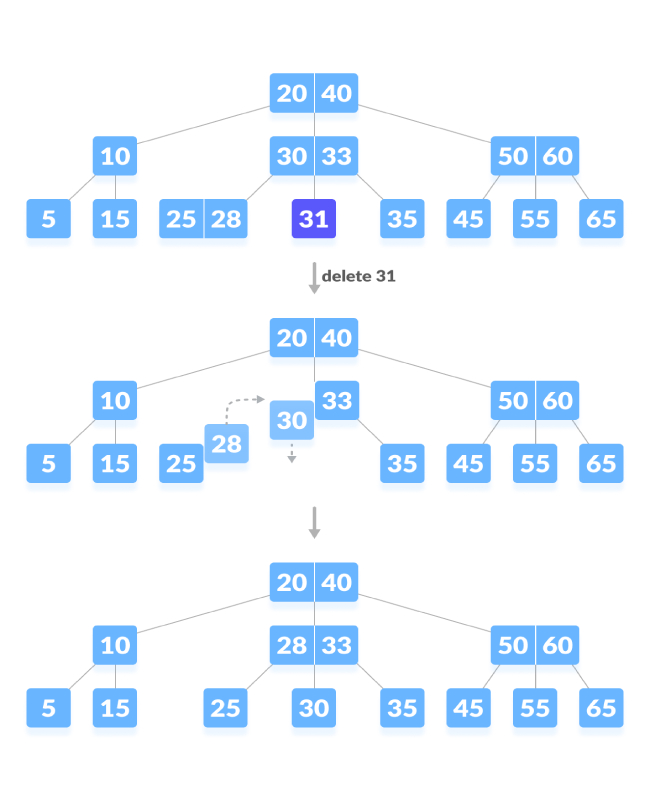
Situation de sous-versement.

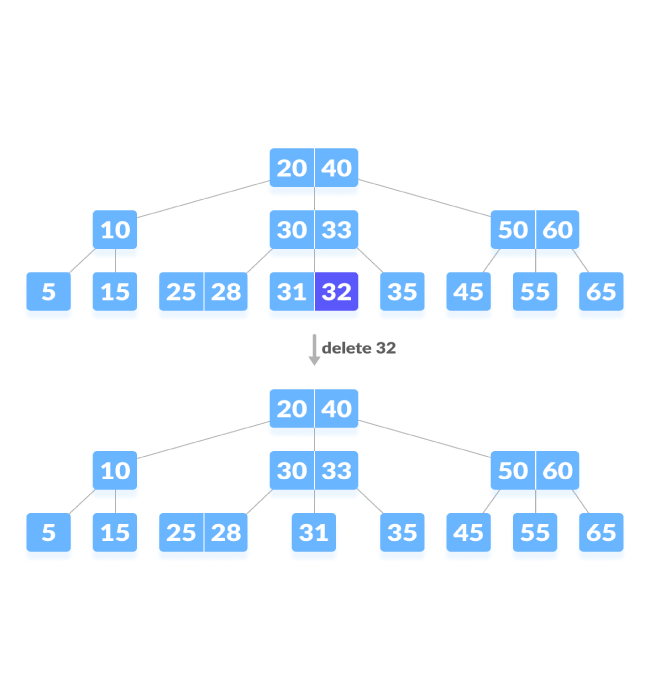
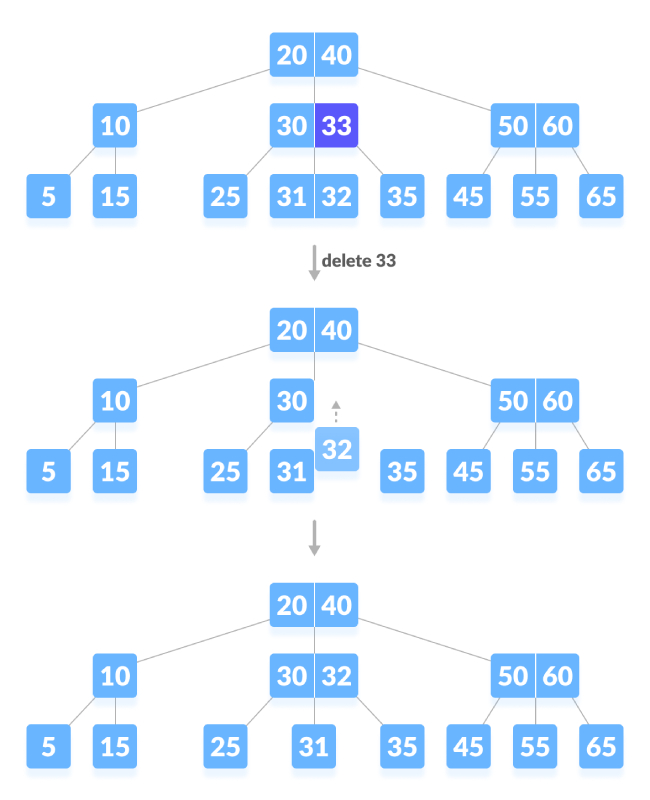
Supprimer les nœuds internes.

Python implémente l'opération de suppression d'arbre B

# B树节点
class BTreeNode:
    def __init__(self, leaf=False):
        self.leaf = leaf
        self.keys = []
        self.child = []

class BTree:
    def __init__(self, t):
        self.root = BTreeNode(True)
        self.t = t

    # 插入元素
    def insert(self, k):
        root = self.root
        if len(root.keys) == (2 * self.t) - 1:
            temp = BTreeNode()
            self.root = temp
            temp.child.insert(0, root)
            self.split_child(temp, 0)
            self.insert_non_full(temp, k)
        else:
            self.insert_non_full(root, k)

    def insert_non_full(self, x, k):
        i = len(x.keys) - 1
        if x.leaf:
            x.keys.append((None, None))
            while i >= 0 and k[0] < x.keys[i][0]:
                x.keys[i + 1] = x.keys[i]
                i -= 1
            x.keys[i + 1] = k
        else:
            while i >= 0 and k[0] < x.keys[i][0]:
                i -= 1
            i += 1
            if len(x.child[i].keys) == (2 * self.t) - 1:
                self.split_child(x, i)
                if k[0] > x.keys[i][0]:
                    i += 1
            self.insert_non_full(x.child[i], k)

    # 分开子节点
    def split_child(self, x, i):
        t = self.t
        y = x.child[i]
        z = BTreeNode(y.leaf)
        x.child.insert(i + 1, z)
        x.keys.insert(i, y.keys[t - 1])
        z.keys = y.keys[t: (2 * t) - 1]
        y.keys = y.keys[0: t - 1]
        if not y.leaf:
            z.child = y.child[t: 2 * t]
            y.child = y.child[0: t - 1]

    # 删除节点
    def delete(self, x, k):
        t = self.t
        i = 0
        while i < len(x.keys) and k[0] > x.keys[i][0]:
            i += 1
        if x.leaf:
            if i < len(x.keys) and x.keys[i][0] == k[0]:
                x.keys.pop(i)
                return
            return

        if i < len(x.keys) and x.keys[i][0] == k[0]:
            return self.delete_internal_node(x, k, i)
        elif len(x.child[i].keys) >= t:
            self.delete(x.child[i], k)
        else:
            if i != 0 and i + 2 < len(x.child):
                if len(x.child[i - 1].keys) >= t:
                    self.delete_sibling(x, i, i - 1)
                elif len(x.child[i + 1].keys) >= t:
                    self.delete_sibling(x, i, i + 1)
                else:
                    self.delete_merge(x, i, i + 1)
            elif i == 0:
                if len(x.child[i + 1].keys) >= t:
                    self.delete_sibling(x, i, i + 1)
                else:
                    self.delete_merge(x, i, i + 1)
            elif i + 1 == len(x.child):
                if len(x.child[i - 1].keys) >= t:
                    self.delete_sibling(x, i, i - 1)
                else:
                    self.delete_merge(x, i, i - 1)
            self.delete(x.child[i], k)

    # 删除节点
    def delete_internal_node(self, x, k, i):
        t = self.t
        if x.leaf:
            if x.keys[i][0] == k[0]:
                x.keys.pop(i)
                return
            return

        if len(x.child[i].keys) >= t:
            x.keys[i] = self.delete_predecessor(x.child[i])
            return
        elif len(x.child[i + 1].keys) >= t:
            x.keys[i] = self.delete_successor(x.child[i + 1])
            return
        else:
            self.delete_merge(x, i, i + 1)
            self.delete_internal_node(x.child[i], k, self.t - 1)

    # 删除前节点
    def delete_predecessor(self, x):
        if x.leaf:
            return x.pop()
        n = len(x.keys) - 1
        if len(x.child[n].keys) >= self.t:
            self.delete_sibling(x, n + 1, n)
        else:
            self.delete_merge(x, n, n + 1)
        self.delete_predecessor(x.child[n])

    # 删除继任节点
    def delete_successor(self, x):
        if x.leaf:
            return x.keys.pop(0)
        if len(x.child[1].keys) >= self.t:
            self.delete_sibling(x, 0, 1)
        else:
            self.delete_merge(x, 0, 1)
        self.delete_successor(x.child[0])

    def delete_merge(self, x, i, j):
        cnode = x.child[i]

        if j > i:
            rsnode = x.child[j]
            cnode.keys.append(x.keys[i])
            for k in range(len(rsnode.keys)):
                cnode.keys.append(rsnode.keys[k])
                if len(rsnode.child) > 0:
                    cnode.child.append(rsnode.child[k])
            if len(rsnode.child) > 0:
                cnode.child.append(rsnode.child.pop())
            new = cnode
            x.keys.pop(i)
            x.child.pop(j)
        else:
            lsnode = x.child[j]
            lsnode.keys.append(x.keys[j])
            for i in range(len(cnode.keys)):
                lsnode.keys.append(cnode.keys[i])
                if len(lsnode.child) > 0:
                    lsnode.child.append(cnode.child[i])
            if len(lsnode.child) > 0:
                lsnode.child.append(cnode.child.pop())
            new = lsnode
            x.keys.pop(j)
            x.child.pop(i)

        if x == self.root and len(x.keys) == 0:
            self.root = new

    # 删除同一级的其他子节点
    def delete_sibling(self, x, i, j):
        cnode = x.child[i]
        if i < j:
            rsnode = x.child[j]
            cnode.keys.append(x.keys[i])
            x.keys[i] = rsnode.keys[0]
            if len(rsnode.child) > 0:
                cnode.child.append(rsnode.child[0])
                rsnode.child.pop(0)
            rsnode.keys.pop(0)
        else:
            lsnode = x.child[j]
            cnode.keys.insert(0, x.keys[i - 1])
            x.keys[i - 1] = lsnode.keys.pop()
            if len(lsnode.child) > 0:
                cnode.child.insert(0, lsnode.child.pop())

    # 输出B树
    def print_tree(self, x, l=0):
        print("Level ", l, " ", len(x.keys), end=":")
        for i in x.keys:
            print(i, end=" ")
        print()
        l += 1
        if len(x.child) > 0:
            for i in x.child:
                self.print_tree(i, l)

B = BTree(3)

for i in range(10):
    B.insert((i, 2 * i))

B.print_tree(B.root)
B.delete(B.root, (8,))
print("\n")
B.print_tree(B.root)

Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!