 tutoriels informatiques
tutoriels informatiques
 connaissances en informatique
connaissances en informatique
 Méthode d'implémentation Matlab et affichage graphique de solutions numériques et analytiques au problème de valeur initiale d'équations différentielles dans un intervalle
Méthode d'implémentation Matlab et affichage graphique de solutions numériques et analytiques au problème de valeur initiale d'équations différentielles dans un intervalle
Méthode d'implémentation Matlab et affichage graphique de solutions numériques et analytiques au problème de valeur initiale d'équations différentielles dans un intervalle
Utilisez Matlab pour résoudre le problème de la valeur initiale des équations différentielles. La solution numérique et la plage de solutions analytiques sont des intervalles et dessinées .
Utilisez Matlab pour résoudre l'équation différentielle 5261, solution numérique, problème de valeur initiale 4102 et solution analytique, vous pouvez le gérer comme ceci :
1.Solution numérique
La solution numérique au problème de la valeur initiale des équations différentielles peut être résolue à l'aide de la fonction ode.
Tout d'abord, personnalisez la fonction de l'équation différentielle, c'est-à-dire
dy = 3/x*y+x^3*(exp(x)+cos(x))-2*x;
Deuxièmement, déterminez les conditions initiales, c'est-à-dire
y0=[(exp(pi)+2/pi)*pi^3];
Troisièmement, utilisez la fonction ode45 pour trouver sa solution numérique [x, y]
2.Solution analytique
La solution analytique du problème de la valeur initiale des équations différentielles peut être résolue à l'aide de la fonction dsolve.
Tout d'abord, déclarez une variable pour y(x), c'est-à-dire
syms y(x)
Deuxièmement, la dérivée première de y(x), qui est
Dy=diff(y,1)
Troisièmement, utilisez la fonction dsolve pour trouver l'expression de sa solution analytique y(x)
y=dsolve(Dy==3/x*y+x^3*(exp(x)+cos(x))-2*x,y(pi)==(exp(pi)+2/pi) *pi^3)
3. Dessinez des courbes de solution numérique et de solution analytique
Tout d'abord, utilisez la fonction plot pour tracer la courbe de la solution numérique
intrigue (x.y)
Deuxièmement, calculez la valeur y qui est équivalente à y pour une série de valeurs de x dans l'intervalle [π, 2π]
Troisièmement, utilisez la fonction plot pour tracer la courbe de la solution analytique
Après avoir exécuté le code, vous pouvez obtenir les résultats suivants.
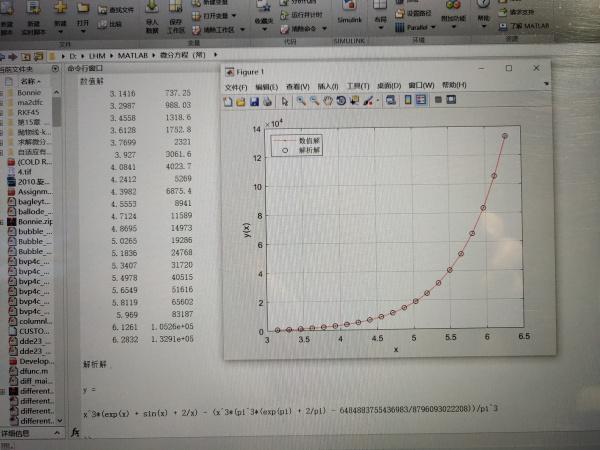
problème Matlab
%%%%%%%%%%%%%%%%%%%% programme source
i=0;equ=0;sum=0;
data=input('veuillez saisir le numéro : ');
pendant(données~=0)
somme=somme+données;
key=input('veuillez continuer : ');
data=clé;
i=i+1;
fin
equ=somme/i;
equ,sum
%%%%%%%%%%%%%%%%%%%%%%%%%
Résultat de l'exécution :
veuillez saisir le numéro : 1
continuez s'il vous plaît : 2
continuez s'il vous plaît : 3
continuez s'il vous plaît : 4
continuez s'il vous plaît : 5
continuez s'il vous plaît : 0
equ =
3
somme =
15
Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!

Outils d'IA chauds

Undresser.AI Undress
Application basée sur l'IA pour créer des photos de nu réalistes

AI Clothes Remover
Outil d'IA en ligne pour supprimer les vêtements des photos.

Undress AI Tool
Images de déshabillage gratuites

Clothoff.io
Dissolvant de vêtements AI

AI Hentai Generator
Générez AI Hentai gratuitement.

Article chaud

Outils chauds

Bloc-notes++7.3.1
Éditeur de code facile à utiliser et gratuit

SublimeText3 version chinoise
Version chinoise, très simple à utiliser

Envoyer Studio 13.0.1
Puissant environnement de développement intégré PHP

Dreamweaver CS6
Outils de développement Web visuel

SublimeText3 version Mac
Logiciel d'édition de code au niveau de Dieu (SublimeText3)

Sujets chauds
 Comment résoudre le code d'erreur Windows & quot; invalid_data_access_trap & quot; (0x00000004)
Mar 11, 2025 am 11:26 AM
Comment résoudre le code d'erreur Windows & quot; invalid_data_access_trap & quot; (0x00000004)
Mar 11, 2025 am 11:26 AM
Cet article aborde l'erreur Windows "invalid_data_access_trap" (0x00000004), un BSOD critique. Il explore les causes communes comme les pilotes défectueux, les dysfonctionnements matériels (RAM, le disque dur), les conflits logiciels, l'overclocking et les logiciels malveillants. Trou
 ENE SYS ENTRETIEN: Conseils et astuces pour maintenir votre système en douceur
Mar 07, 2025 pm 03:09 PM
ENE SYS ENTRETIEN: Conseils et astuces pour maintenir votre système en douceur
Mar 07, 2025 pm 03:09 PM
Cet article fournit des conseils pratiques pour maintenir les systèmes ENE SYS. Il traite des problèmes courants comme la surchauffe et la corruption des données, offrant des mesures préventives telles que le nettoyage régulier, les sauvegardes et les mises à jour logicielles. Une maintenance sur mesure s
 5 erreurs courantes à éviter pendant la mise en œuvre de l'ene sys
Mar 07, 2025 pm 03:11 PM
5 erreurs courantes à éviter pendant la mise en œuvre de l'ene sys
Mar 07, 2025 pm 03:11 PM
Cet article identifie cinq pièges communs dans la mise en œuvre de l'ene SYS: planification insuffisante, formation inadéquate des utilisateurs, migration inappropriée des données, négligence en matière de sécurité et tests insuffisants. Ces erreurs peuvent entraîner des retards de projet, des défaillances du système
 Comment modifier le registre? (Avertissement: utilisez avec prudence!)
Mar 21, 2025 pm 07:46 PM
Comment modifier le registre? (Avertissement: utilisez avec prudence!)
Mar 21, 2025 pm 07:46 PM
L'article traite de l'édition du registre Windows, des précautions, des méthodes de sauvegarde et des problèmes potentiels des modifications incorrectes. Problème principal: risques d'instabilité du système et de perte de données contre les modifications inappropriées.
 Découvrez comment réparer l'avertissement de santé dans les paramètres Windows
Mar 19, 2025 am 11:10 AM
Découvrez comment réparer l'avertissement de santé dans les paramètres Windows
Mar 19, 2025 am 11:10 AM
Que signifie l'avertissement de santé des motivations dans les paramètres Windows et que devez-vous faire lorsque vous recevez l'avertissement de disque? Lisez ce tutoriel Php.CN pour obtenir des instructions étape par étape pour faire face à cette situation.
 Comment gérer les services dans Windows?
Mar 21, 2025 pm 07:52 PM
Comment gérer les services dans Windows?
Mar 21, 2025 pm 07:52 PM
L'article discute de la gestion des services Windows pour la santé du système, y compris le démarrage, l'arrêt, le redémarrage des services et les meilleures pratiques de stabilité.
 Quelle application utilise ene.sys
Mar 12, 2025 pm 01:25 PM
Quelle application utilise ene.sys
Mar 12, 2025 pm 01:25 PM
Cet article identifie ENE.SYS comme un composant de pilote audio haute définition Realtek. Il détaille sa fonction dans la gestion du matériel audio, mettant l'accent sur son rôle crucial dans la fonctionnalité audio. L'article guide également les utilisateurs sur la vérification de sa légitimité
 Pourquoi le Driver Asio.sys ne charge-t-il pas
Mar 10, 2025 pm 07:58 PM
Pourquoi le Driver Asio.sys ne charge-t-il pas
Mar 10, 2025 pm 07:58 PM
Cet article traite de l'échec du pilote audio Windows Asio.sys. Les causes courantes incluent les fichiers système corrompus, l'incompatibilité matérielle / pilote, les conflits logiciels, les problèmes de registre et les logiciels malveillants. Le dépannage implique des scans SFC, le pilote Upda





