 base de données
base de données
 tutoriel mysql
tutoriel mysql
 Schéma de principe de l'implémentation Python de l'algorithme d'insertion de B-tree
Schéma de principe de l'implémentation Python de l'algorithme d'insertion de B-tree
Schéma de principe de l'implémentation Python de l'algorithme d'insertion de B-tree
B-tree est un arbre de recherche binaire hautement équilibré. Pour effectuer une opération d'insertion, vous devez d'abord obtenir la position du nœud inséré pour qu'il soit plus grand que le sous-arbre de gauche et plus petit que le sous-arbre de droite lors de la division. nécessaire.
Comprendre le principe de fonctionnement de l'insertion d'un arbre B avec une seule image

Algorithme d'insertion d'un arbre B
<code>BreeInsertion(T, k)r root[T]if n[r] = 2t - 1<br/> s = AllocateNode()<br/> root[T] = s<br/> leaf[s] = FALSE<br/> n[s] <- 0<br/> c1[s] <- r<br/> BtreeSplitChild(s, 1, r)<br/> BtreeInsertNonFull(s, k)else BtreeInsertNonFull(r, k)BtreeInsertNonFull(x, k)i = n[x]if leaf[x]<br/> while i ≥ 1 and k < keyi[x]<br/> keyi+1 [x] = keyi[x]<br/> i = i - 1<br/> keyi+1[x] = k<br/> n[x] = n[x] + 1else while i ≥ 1 and k < keyi[x]<br/> i = i - 1<br/> i = i + 1<br/> if n[ci[x]] == 2t - 1<br/> BtreeSplitChild(x, i, ci[x])<br/> if k &rt; keyi[x]<br/> i = i + 1<br/> BtreeInsertNonFull(ci[x], k)BtreeSplitChild(x, i)BtreeSplitChild(x, i, y)z = AllocateNode()leaf[z] = leaf[y]n[z] = t - 1for j = 1 to t - 1<br/> keyj[z] = keyj+t[y]if not leaf [y]<br/> for j = 1 to t<br/> cj[z] = cj + t[y]n[y] = t - 1for j = n[x] + 1 to i + 1<br/> cj+1[x] = cj[x]ci+1[x] = zfor j = n[x] to i<br/> keyj+1[x] = keyj[x]keyi[x] = keyt[y]n[x] = n[x] + 1</code>
Utiliser Python pour implémenter l'algorithme d'insertion d'un arbre B
<code>class BTreeNode:<br/> def __init__(self, leaf=False):<br/> self.leaf = leaf<br/> self.keys = []<br/> self.child = []<br/> <br/>class BTree:<br/> def __init__(self, t):<br/> self.root = BTreeNode(True)<br/> self.t = t<br/> <br/> def insert(self, k):<br/> root = self.root<br/> if len(root.keys) == (2 * self.t) - 1:<br/> temp = BTreeNode()<br/> self.root = temp<br/> temp.child.insert(0, root)<br/> self.split_child(temp, 0)<br/> self.insert_non_full(temp, k)<br/> else:<br/> self.insert_non_full(root, k)<br/> <br/> def insert_non_full(self, x, k):<br/> i = len(x.keys) - 1<br/> if x.leaf:<br/> x.keys.append((None, None))<br/> while i >= 0 and k[0] < x.keys[i][0]:<br/> x.keys[i + 1] = x.keys[i]<br/> i -= 1<br/> x.keys[i + 1] = k<br/> else:<br/> while i >= 0 and k[0] < x.keys[i][0]:<br/> i -= 1<br/> i += 1<br/> if len(x.child[i].keys) == (2 * self.t) - 1:<br/> self.split_child(x, i)<br/> if k[0] > x.keys[i][0]:<br/> i += 1<br/> self.insert_non_full(x.child[i], k)<br/> <br/> def split_child(self, x, i):<br/> t = self.t<br/> y = x.child[i]<br/> z = BTreeNode(y.leaf)<br/> x.child.insert(i + 1, z)<br/> x.keys.insert(i, y.keys[t - 1])<br/> z.keys = y.keys[t: (2 * t) - 1]<br/> y.keys = y.keys[0: t - 1]<br/> if not y.leaf:<br/> z.child = y.child[t: 2 * t]<br/> y.child = y.child[0: t - 1]<br/> <br/> def print_tree(self, x, l=0):<br/> print("Level ", l, " ", len(x.keys), end=":")<br/> for i in x.keys:<br/> print(i, end=" ")<br/> print()<br/> l += 1<br/> if len(x.child) > 0:<br/> for i in x.child:<br/> self.print_tree(i, l)<br/> <br/>def main():<br/> B = BTree(3)<br/> <br/> for i in range(10):<br/> B.insert((i, 2 * i))<br/> <br/> B.print_tree(B.root)<br/> <br/>if __name__ == '__main__':<br/> main()</code>Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!

Outils d'IA chauds

Undresser.AI Undress
Application basée sur l'IA pour créer des photos de nu réalistes

AI Clothes Remover
Outil d'IA en ligne pour supprimer les vêtements des photos.

Undress AI Tool
Images de déshabillage gratuites

Clothoff.io
Dissolvant de vêtements AI

Video Face Swap
Échangez les visages dans n'importe quelle vidéo sans effort grâce à notre outil d'échange de visage AI entièrement gratuit !

Article chaud

Outils chauds

Bloc-notes++7.3.1
Éditeur de code facile à utiliser et gratuit

SublimeText3 version chinoise
Version chinoise, très simple à utiliser

Envoyer Studio 13.0.1
Puissant environnement de développement intégré PHP

Dreamweaver CS6
Outils de développement Web visuel

SublimeText3 version Mac
Logiciel d'édition de code au niveau de Dieu (SublimeText3)

Sujets chauds
 1662
1662
 14
14
 1418
1418
 52
52
 1311
1311
 25
25
 1261
1261
 29
29
 1234
1234
 24
24
 Quand une analyse de table complète pourrait-elle être plus rapide que d'utiliser un index dans MySQL?
Apr 09, 2025 am 12:05 AM
Quand une analyse de table complète pourrait-elle être plus rapide que d'utiliser un index dans MySQL?
Apr 09, 2025 am 12:05 AM
La numérisation complète de la table peut être plus rapide dans MySQL que l'utilisation d'index. Les cas spécifiques comprennent: 1) le volume de données est petit; 2) Lorsque la requête renvoie une grande quantité de données; 3) Lorsque la colonne d'index n'est pas très sélective; 4) Lorsque la requête complexe. En analysant les plans de requête, en optimisant les index, en évitant le sur-index et en maintenant régulièrement des tables, vous pouvez faire les meilleurs choix dans les applications pratiques.
 Puis-je installer mysql sur Windows 7
Apr 08, 2025 pm 03:21 PM
Puis-je installer mysql sur Windows 7
Apr 08, 2025 pm 03:21 PM
Oui, MySQL peut être installé sur Windows 7, et bien que Microsoft ait cessé de prendre en charge Windows 7, MySQL est toujours compatible avec lui. Cependant, les points suivants doivent être notés lors du processus d'installation: téléchargez le programme d'installation MySQL pour Windows. Sélectionnez la version appropriée de MySQL (communauté ou entreprise). Sélectionnez le répertoire d'installation et le jeu de caractères appropriés pendant le processus d'installation. Définissez le mot de passe de l'utilisateur racine et gardez-le correctement. Connectez-vous à la base de données pour les tests. Notez les problèmes de compatibilité et de sécurité sur Windows 7, et il est recommandé de passer à un système d'exploitation pris en charge.
 Mysql et Mariadb peuvent-ils coexister
Apr 08, 2025 pm 02:27 PM
Mysql et Mariadb peuvent-ils coexister
Apr 08, 2025 pm 02:27 PM
MySQL et MARIADB peuvent coexister, mais doivent être configurés avec prudence. La clé consiste à allouer différents numéros de port et répertoires de données à chaque base de données et ajuster les paramètres tels que l'allocation de mémoire et la taille du cache. La mise en commun de la connexion, la configuration des applications et les différences de version doivent également être prises en compte et doivent être soigneusement testées et planifiées pour éviter les pièges. L'exécution de deux bases de données simultanément peut entraîner des problèmes de performances dans les situations où les ressources sont limitées.
 MySQL: Concepts simples pour l'apprentissage facile
Apr 10, 2025 am 09:29 AM
MySQL: Concepts simples pour l'apprentissage facile
Apr 10, 2025 am 09:29 AM
MySQL est un système de gestion de base de données relationnel open source. 1) Créez une base de données et des tables: utilisez les commandes CreateDatabase et CreateTable. 2) Opérations de base: insérer, mettre à jour, supprimer et sélectionner. 3) Opérations avancées: jointure, sous-requête et traitement des transactions. 4) Compétences de débogage: vérifiez la syntaxe, le type de données et les autorisations. 5) Suggestions d'optimisation: utilisez des index, évitez de sélectionner * et utilisez les transactions.
 Intégration RDS MySQL avec Redshift Zero ETL
Apr 08, 2025 pm 07:06 PM
Intégration RDS MySQL avec Redshift Zero ETL
Apr 08, 2025 pm 07:06 PM
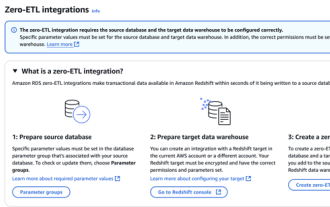
Simplification de l'intégration des données: AmazonrDSMysQL et l'intégration Zero ETL de Redshift, l'intégration des données est au cœur d'une organisation basée sur les données. Les processus traditionnels ETL (extrait, converti, charge) sont complexes et prennent du temps, en particulier lors de l'intégration de bases de données (telles que AmazonrDSMysQL) avec des entrepôts de données (tels que Redshift). Cependant, AWS fournit des solutions d'intégration ETL Zero qui ont complètement changé cette situation, fournissant une solution simplifiée et à temps proche pour la migration des données de RDSMySQL à Redshift. Cet article plongera dans l'intégration RDSMYSQL ZERO ETL avec Redshift, expliquant comment il fonctionne et les avantages qu'il apporte aux ingénieurs de données et aux développeurs.
 Laravel Eloquent Orm dans Bangla Partial Model Search)
Apr 08, 2025 pm 02:06 PM
Laravel Eloquent Orm dans Bangla Partial Model Search)
Apr 08, 2025 pm 02:06 PM
Laravelelognent Model Retrieval: Faconttement l'obtention de données de base de données Eloquentorm fournit un moyen concis et facile à comprendre pour faire fonctionner la base de données. Cet article présentera en détail diverses techniques de recherche de modèles éloquentes pour vous aider à obtenir efficacement les données de la base de données. 1. Obtenez tous les enregistrements. Utilisez la méthode All () pour obtenir tous les enregistrements dans la table de base de données: usApp \ Modèles \ Post; $ poters = post :: all (); Cela rendra une collection. Vous pouvez accéder aux données à l'aide de Foreach Loop ou d'autres méthodes de collecte: ForEach ($ PostsAs $ POST) {echo $ post->
 La relation entre l'utilisateur de MySQL et la base de données
Apr 08, 2025 pm 07:15 PM
La relation entre l'utilisateur de MySQL et la base de données
Apr 08, 2025 pm 07:15 PM
Dans la base de données MySQL, la relation entre l'utilisateur et la base de données est définie par les autorisations et les tables. L'utilisateur a un nom d'utilisateur et un mot de passe pour accéder à la base de données. Les autorisations sont accordées par la commande Grant, tandis que le tableau est créé par la commande Create Table. Pour établir une relation entre un utilisateur et une base de données, vous devez créer une base de données, créer un utilisateur, puis accorder des autorisations.
 MySQL: la facilité de gestion des données pour les débutants
Apr 09, 2025 am 12:07 AM
MySQL: la facilité de gestion des données pour les débutants
Apr 09, 2025 am 12:07 AM
MySQL convient aux débutants car il est simple à installer, puissant et facile à gérer les données. 1. Installation et configuration simples, adaptées à une variété de systèmes d'exploitation. 2. Prise en charge des opérations de base telles que la création de bases de données et de tables, d'insertion, d'interrogation, de mise à jour et de suppression de données. 3. Fournir des fonctions avancées telles que les opérations de jointure et les sous-questionnaires. 4. Les performances peuvent être améliorées par l'indexation, l'optimisation des requêtes et le partitionnement de la table. 5. Prise en charge des mesures de sauvegarde, de récupération et de sécurité pour garantir la sécurité et la cohérence des données.



