Comprendre la fonction ReLU dans l'apprentissage automatique

Qu'est-ce que la fonction ReLU ?

La fonction ReLU est une fonction mathématique définie comme f(x)=max(0,x), où x est n'importe quel nombre réel. En termes simples, si x est inférieur ou égal à 0, la fonction renvoie 0. Sinon, renvoie x.

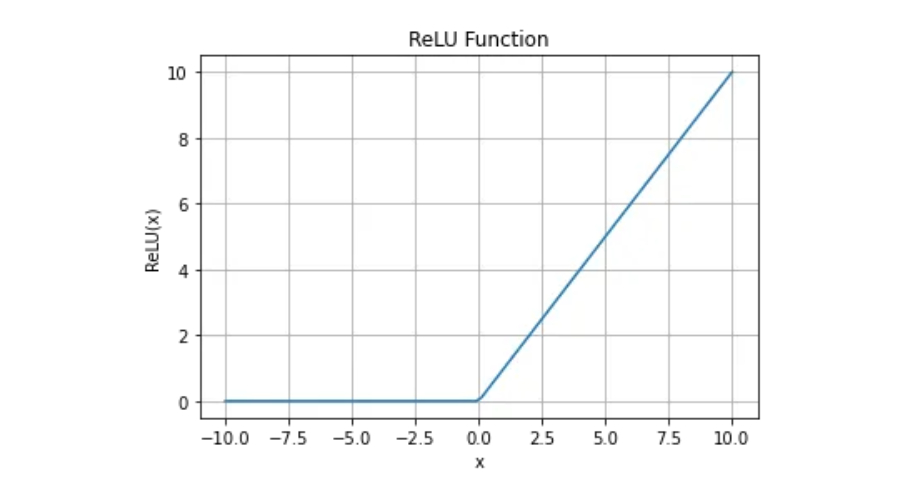
Continuité et différentiabilité de la fonction ReLU

Pour une fonction différentiable, elle doit d'abord être continue. La fonction ReLU satisfait à l'exigence de continuité, mais la dérivée en x=0 n'existe pas, donc la fonction ReLU n'est pas dérivable à ce stade.

Alors pourquoi la fonction ReLU est-elle encore utilisée en deep learning ?

Bien que la fonction ReLU ne soit pas différentiable à x=0, nous pouvons toujours l'appliquer en deep learning en affinant l'algorithme d'optimisation. La descente de gradient est un algorithme d'optimisation utilisé pour minimiser une fonction de coût. Lorsque la fonction ReLU n'a pas de dérivée définie à x=0, nous pouvons la définir sur 0 ou toute autre valeur et continuer le processus d'optimisation. De cette manière, nous pouvons utiliser les caractéristiques non linéaires de la fonction ReLU pour améliorer les performances du modèle d'apprentissage profond.

En général, la fonction d'activation ReLU est l'une des fonctions d'activation les plus populaires dans les réseaux d'apprentissage profond. Sa simplicité et sa grande efficacité de calcul en font un outil important pour améliorer la convergence lors de la formation. Bien qu’il ne soit pas différentiable à x=0, cela n’affecte pas son application en descente de gradient. La fonction ReLU est donc un outil polyvalent et puissant dans le domaine de l’apprentissage automatique.

Avantages de la fonction ReLU

1.

La fonction redresseur est très simple à mettre en œuvre et nécessite une fonction max().

2. Rareté représentationnelle

La représentation clairsemée est une propriété souhaitable dans l'apprentissage des représentations car elle permet d'accélérer l'apprentissage et de simplifier les modèles. Il permet à l'activation de la couche cachée du réseau neuronal de contenir une ou plusieurs vraies valeurs zéro, ce qui signifie que les entrées négatives peuvent également produire de vraies valeurs zéro. Cette capacité permet aux réseaux neuronaux de mieux gérer les données à grande échelle et peut réduire le besoin en ressources informatiques et de stockage. Par conséquent, une représentation clairsemée est très importante pour optimiser les performances et l’efficacité des réseaux de neurones.

3. Comportement linéaire

La fonction redresseur ressemble et se comporte de manière similaire à la fonction d'activation linéaire. Convient pour l'optimisation du comportement linéaire ou quasi-linéaire.

Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!