 Périphériques technologiques
Périphériques technologiques
 IA
IA
 Application de la fonction sigmoïde dans un réseau neuronal artificiel
Application de la fonction sigmoïde dans un réseau neuronal artificiel
Application de la fonction sigmoïde dans un réseau neuronal artificiel

Dans les réseaux de neurones artificiels, la fonction sigmoïde est souvent utilisée comme fonction d'activation des neurones pour introduire des caractéristiques non linéaires. Cela permet aux réseaux neuronaux d'apprendre des limites de décision plus complexes et de jouer un rôle important dans diverses applications telles que la reconnaissance d'images, le traitement du langage naturel et la reconnaissance vocale.
La fonction sigmoïde est une fonction mathématique couramment utilisée qui peut mapper n'importe quelle valeur d'entrée à une valeur comprise entre 0 et 1, elle a donc été largement utilisée dans les problèmes de classification binaire et de régression logistique. Cette fonction est caractérisée par une forme en « S » qui croît lentement au début, puis se rapproche rapidement de 1 et finit par se stabiliser.
Comprendre la fonction sigmoïde
La fonction sigmoïde est une fonction mathématique couramment utilisée pour mapper les valeurs d'entrée sur la plage comprise entre 0 et 1. Sa définition mathématique est 1/(1+e^(-x)), où x est la valeur d'entrée et e est la constante 2,718. Cette fonction est très utile dans les problèmes de classification binaire et de régression logistique. Sa plage de valeurs est (0,1) et son domaine est (-infini, +infini). La caractéristique de la fonction en forme de S est qu'elle peut convertir n'importe quelle entrée réelle en valeur de probabilité, elle est donc souvent utilisée dans la couche de sortie du modèle dans l'apprentissage automatique et les statistiques.
L'une des propriétés clés de la fonction sigmoïde est que sa valeur de sortie présente une courbe en forme de « S » à mesure que la valeur d'entrée augmente. À mesure que la valeur d’entrée augmente, la valeur de sortie augmente progressivement et finit par se rapprocher de 1. Cette fonctionnalité fournit des fonctionnalités importantes pour modéliser les limites de décision dans les problèmes de classification binaire.
Une autre propriété importante de la fonction sigmoïde est sa dérivée, qui joue un rôle clé dans l'entraînement des réseaux neuronaux. La dérivée de la fonction sigmoïde est définie comme f(x)(1-f(x)), où f(x) représente la sortie de la fonction. L'existence de dérivés permet au réseau neuronal d'ajuster plus efficacement les poids et les biais des neurones, améliorant ainsi les performances du réseau. En calculant les dérivées, le réseau peut mettre à jour les paramètres en fonction du gradient de la fonction de perte, permettant ainsi au réseau d'optimiser et d'améliorer progressivement la précision. Cette méthode d'utilisation de dérivés pour entraîner des réseaux est largement utilisée dans le domaine de l'apprentissage profond, permettant aux réseaux de neurones d'apprendre et de s'adapter à une variété de tâches complexes.
En plus de la fonction sigmoïde, il existe d'autres fonctions d'activation, telles que ReLU et tanh, qui peuvent compenser les limitations de la fonction sigmoïde. La sortie de la fonction sigmoïde est toujours comprise entre 0 et 1, ce qui peut poser des problèmes lorsque la sortie du réseau doit être supérieure à 1 ou inférieure à 0. La fonction ReLU peut résoudre ce problème en mappant les nombres négatifs à 0, tandis que les nombres positifs restent inchangés. De plus, la fonction tanh est également une fonction d'activation couramment utilisée. Sa plage de sortie est comprise entre -1 et 1, ce qui est plus flexible que la fonction sigmoïde. Par conséquent, lors de la conception d'un réseau neuronal, différentes fonctions d'activation peuvent être sélectionnées en fonction de besoins spécifiques pour obtenir de meilleurs résultats.
Visualiser la fonction sigmoïde à l'aide de graphiques permet de mieux comprendre ses propriétés. Le graphique montre la forme « S » prise par la fonction et comment la valeur de sortie change à mesure que la valeur d'entrée change.
Fonction sigmoïde dans les réseaux de neurones artificiels
La fonction sigmoïde est généralement utilisée comme fonction d'activation des réseaux de neurones artificiels. Dans un réseau neuronal à action directe, la sortie de chaque neurone est traitée par une fonction sigmoïde, qui peut introduire des caractéristiques non linéaires dans le modèle. L'introduction de caractéristiques non linéaires est importante car elle permet au réseau neuronal d'apprendre des limites de décision plus complexes, améliorant ainsi ses performances sur des tâches spécifiques.
Avantages :
- Produit des valeurs de sortie comprises entre 0 et 1, ce qui aide dans les problèmes de classification binaire et de régression logistique.
- Différenciable signifie que ses dérivées peuvent être calculées, et il est facile d'optimiser le réseau en ajustant les poids et les biais des neurones.
Inconvénients :
- Il peut produire des valeurs de sortie proches de 0 ou 1, ce qui peut causer des problèmes avec l'algorithme d'optimisation.
- Le gradient de la fonction sigmoïde devient très faible près de la valeur de sortie 0 ou 1, ce qui rend difficile pour l'algorithme d'optimisation d'ajuster les poids et les biais des neurones.
Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!

Outils d'IA chauds

Undresser.AI Undress
Application basée sur l'IA pour créer des photos de nu réalistes

AI Clothes Remover
Outil d'IA en ligne pour supprimer les vêtements des photos.

Undress AI Tool
Images de déshabillage gratuites

Clothoff.io
Dissolvant de vêtements AI

AI Hentai Generator
Générez AI Hentai gratuitement.

Article chaud

Outils chauds

Bloc-notes++7.3.1
Éditeur de code facile à utiliser et gratuit

SublimeText3 version chinoise
Version chinoise, très simple à utiliser

Envoyer Studio 13.0.1
Puissant environnement de développement intégré PHP

Dreamweaver CS6
Outils de développement Web visuel

SublimeText3 version Mac
Logiciel d'édition de code au niveau de Dieu (SublimeText3)
 Explorez les concepts, les différences, les avantages et les inconvénients de RNN, LSTM et GRU
Jan 22, 2024 pm 07:51 PM
Explorez les concepts, les différences, les avantages et les inconvénients de RNN, LSTM et GRU
Jan 22, 2024 pm 07:51 PM
Dans les données de séries chronologiques, il existe des dépendances entre les observations, elles ne sont donc pas indépendantes les unes des autres. Cependant, les réseaux de neurones traditionnels traitent chaque observation comme indépendante, ce qui limite la capacité du modèle à modéliser des données de séries chronologiques. Pour résoudre ce problème, le réseau neuronal récurrent (RNN) a été introduit, qui a introduit le concept de mémoire pour capturer les caractéristiques dynamiques des données de séries chronologiques en établissant des dépendances entre les points de données du réseau. Grâce à des connexions récurrentes, RNN peut transmettre des informations antérieures à l'observation actuelle pour mieux prédire les valeurs futures. Cela fait de RNN un outil puissant pour les tâches impliquant des données de séries chronologiques. Mais comment RNN parvient-il à obtenir ce type de mémoire ? RNN réalise la mémoire via la boucle de rétroaction dans le réseau neuronal. C'est la différence entre RNN et le réseau neuronal traditionnel.
 Calcul des opérandes à virgule flottante (FLOPS) pour les réseaux de neurones
Jan 22, 2024 pm 07:21 PM
Calcul des opérandes à virgule flottante (FLOPS) pour les réseaux de neurones
Jan 22, 2024 pm 07:21 PM
FLOPS est l'une des normes d'évaluation des performances informatiques, utilisée pour mesurer le nombre d'opérations en virgule flottante par seconde. Dans les réseaux de neurones, FLOPS est souvent utilisé pour évaluer la complexité informatique du modèle et l'utilisation des ressources informatiques. C'est un indicateur important utilisé pour mesurer la puissance de calcul et l'efficacité d'un ordinateur. Un réseau de neurones est un modèle complexe composé de plusieurs couches de neurones utilisées pour des tâches telles que la classification, la régression et le clustering des données. La formation et l'inférence des réseaux de neurones nécessitent un grand nombre de multiplications matricielles, de convolutions et d'autres opérations de calcul, la complexité de calcul est donc très élevée. FLOPS (FloatingPointOperationsperSecond) peut être utilisé pour mesurer la complexité de calcul des réseaux de neurones afin d'évaluer l'efficacité d'utilisation des ressources de calcul du modèle. FIASCO
 Définition et analyse structurelle du réseau neuronal flou
Jan 22, 2024 pm 09:09 PM
Définition et analyse structurelle du réseau neuronal flou
Jan 22, 2024 pm 09:09 PM
Le réseau de neurones flous est un modèle hybride qui combine la logique floue et les réseaux de neurones pour résoudre des problèmes flous ou incertains difficiles à gérer avec les réseaux de neurones traditionnels. Sa conception s'inspire du flou et de l'incertitude de la cognition humaine, c'est pourquoi il est largement utilisé dans les systèmes de contrôle, la reconnaissance de formes, l'exploration de données et d'autres domaines. L'architecture de base du réseau neuronal flou se compose d'un sous-système flou et d'un sous-système neuronal. Le sous-système flou utilise la logique floue pour traiter les données d'entrée et les convertir en ensembles flous pour exprimer le flou et l'incertitude des données d'entrée. Le sous-système neuronal utilise des réseaux de neurones pour traiter des ensembles flous pour des tâches telles que la classification, la régression ou le clustering. L'interaction entre le sous-système flou et le sous-système neuronal confère au réseau neuronal flou des capacités de traitement plus puissantes et peut
 Une étude de cas sur l'utilisation du modèle LSTM bidirectionnel pour la classification de texte
Jan 24, 2024 am 10:36 AM
Une étude de cas sur l'utilisation du modèle LSTM bidirectionnel pour la classification de texte
Jan 24, 2024 am 10:36 AM
Le modèle LSTM bidirectionnel est un réseau neuronal utilisé pour la classification de texte. Vous trouverez ci-dessous un exemple simple montrant comment utiliser le LSTM bidirectionnel pour les tâches de classification de texte. Tout d'abord, nous devons importer les bibliothèques et modules requis : importosimportnumpyasnpfromkeras.preprocessing.textimportTokenizerfromkeras.preprocessing.sequenceimportpad_sequencesfromkeras.modelsimportSequentialfromkeras.layersimportDense,Em
 Débruitage d'image à l'aide de réseaux de neurones convolutifs
Jan 23, 2024 pm 11:48 PM
Débruitage d'image à l'aide de réseaux de neurones convolutifs
Jan 23, 2024 pm 11:48 PM
Les réseaux de neurones convolutifs fonctionnent bien dans les tâches de débruitage d'images. Il utilise les filtres appris pour filtrer le bruit et restaurer ainsi l'image originale. Cet article présente en détail la méthode de débruitage d'image basée sur un réseau neuronal convolutif. 1. Présentation du réseau neuronal convolutif Le réseau neuronal convolutif est un algorithme d'apprentissage en profondeur qui utilise une combinaison de plusieurs couches convolutives, des couches de regroupement et des couches entièrement connectées pour apprendre et classer les caractéristiques de l'image. Dans la couche convolutive, les caractéristiques locales de l'image sont extraites via des opérations de convolution, capturant ainsi la corrélation spatiale dans l'image. La couche de pooling réduit la quantité de calcul en réduisant la dimension des fonctionnalités et conserve les principales fonctionnalités. La couche entièrement connectée est responsable du mappage des fonctionnalités et des étiquettes apprises pour mettre en œuvre la classification des images ou d'autres tâches. La conception de cette structure de réseau rend les réseaux de neurones convolutifs utiles dans le traitement et la reconnaissance d'images.
 Réseau de neurones jumeaux : analyse des principes et des applications
Jan 24, 2024 pm 04:18 PM
Réseau de neurones jumeaux : analyse des principes et des applications
Jan 24, 2024 pm 04:18 PM
Le réseau neuronal siamois est une structure de réseau neuronal artificiel unique. Il se compose de deux réseaux de neurones identiques partageant les mêmes paramètres et poids. Dans le même temps, les deux réseaux partagent également les mêmes données d’entrée. Cette conception a été inspirée par des jumeaux, car les deux réseaux de neurones sont structurellement identiques. Le principe du réseau neuronal siamois est d'accomplir des tâches spécifiques, telles que la correspondance d'images, la correspondance de textes et la reconnaissance de visages, en comparant la similitude ou la distance entre deux données d'entrée. Pendant la formation, le réseau tente de mapper des données similaires vers des régions adjacentes et des données différentes vers des régions distantes. De cette manière, le réseau peut apprendre à classer ou à faire correspondre différentes données pour obtenir des résultats correspondants.
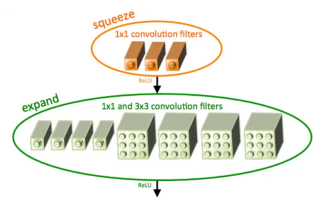 Introduction à SqueezeNet et ses caractéristiques
Jan 22, 2024 pm 07:15 PM
Introduction à SqueezeNet et ses caractéristiques
Jan 22, 2024 pm 07:15 PM
SqueezeNet est un algorithme petit et précis qui établit un bon équilibre entre haute précision et faible complexité, ce qui le rend idéal pour les systèmes mobiles et embarqués aux ressources limitées. En 2016, des chercheurs de DeepScale, de l'Université de Californie à Berkeley et de l'Université de Stanford ont proposé SqueezeNet, un réseau neuronal convolutif (CNN) compact et efficace. Ces dernières années, les chercheurs ont apporté plusieurs améliorations à SqueezeNet, notamment SqueezeNetv1.1 et SqueezeNetv2.0. Les améliorations apportées aux deux versions augmentent non seulement la précision, mais réduisent également les coûts de calcul. Précision de SqueezeNetv1.1 sur l'ensemble de données ImageNet
 réseau neuronal convolutif causal
Jan 24, 2024 pm 12:42 PM
réseau neuronal convolutif causal
Jan 24, 2024 pm 12:42 PM
Le réseau neuronal convolutif causal est un réseau neuronal convolutif spécial conçu pour les problèmes de causalité dans les données de séries chronologiques. Par rapport aux réseaux de neurones convolutifs conventionnels, les réseaux de neurones convolutifs causals présentent des avantages uniques en ce qu'ils conservent la relation causale des séries chronologiques et sont largement utilisés dans la prédiction et l'analyse des données de séries chronologiques. L'idée centrale du réseau neuronal convolutionnel causal est d'introduire la causalité dans l'opération de convolution. Les réseaux neuronaux convolutifs traditionnels peuvent percevoir simultanément les données avant et après le point temporel actuel, mais dans la prévision des séries chronologiques, cela peut entraîner des problèmes de fuite d'informations. Parce que le résultat de la prédiction à l’heure actuelle sera affecté par les données à l’heure future. Le réseau neuronal convolutionnel causal résout ce problème. Il ne peut percevoir que le point temporel actuel et les données précédentes, mais ne peut pas percevoir les données futures.





