 développement back-end
développement back-end
 Tutoriel Python
Tutoriel Python
 Étapes détaillées pour implémenter le parcours dans l'ordre de la pile d'un arbre binaire à l'aide de Python
Étapes détaillées pour implémenter le parcours dans l'ordre de la pile d'un arbre binaire à l'aide de Python
Étapes détaillées pour implémenter le parcours dans l'ordre de la pile d'un arbre binaire à l'aide de Python

使用堆栈无需递归就能遍历二叉树,下面是一个使用堆栈中序遍历二叉树的算法。
算法思路
1)创建一个空栈S。
2)将当前节点初始化为root
3)将当前节点推入S并设置current=current->left直到current为NULL
4)如果current为NULL且堆栈不为空,则
a)从堆栈中弹出顶部项目。
b)输出弹出的项目,设置current=popped_item->right
c)转到步骤3)。
5)如果current为NULL并且stack为空,那么算法结束。
算法实现步骤
1
/\
2 3
/\
4 5
步骤1创建一个空堆栈:S=NULL
步骤2将current设置为root的地址:current->1
步骤3推送当前节点并设置current=current->left
直到当前为NULL
当前->1
推1:堆栈S->1
当前->2
推2:堆栈>2,1
当前->4
推4:堆栈S>4、2、1
当前=NULL
步骤4从S弹出
a)弹出4:堆栈S->2,1
b)打印“4”
c)current=NULL/*right of 4*/并转到步骤3
由于current is NULL step 3没有做任何事情。
步骤4再次弹出。
a)弹出2:堆栈S->1
b)打印“2”
c)current->;5/*right of 2*/并转到步骤3
第3步将5推入堆栈并使当前为NULL
堆栈S->5,1
当前=NULL
步骤4从S弹出
a)弹出5:堆栈S->1
b)打印“5”
c)current=NULL/*right of 5*/并转到步骤3
由于current is NULL step 3没有做任何事情
步骤4再次弹出。
a)弹出1:堆栈S->NULL
b)打印“1”
c)当前->3/*1的右边*/
第3步将3推入堆栈并使当前为NULL
堆栈S->3
当前=NULL
步骤4从S弹出
a)弹出3:堆栈S->NULL
b)打印“3”
c)current=NULL/*3的右边*/
由于堆栈S为空且当前为NULL,因此遍历已完成。
Python实现堆栈中序遍历二叉树
class Node: def __init__(self,data): self.data=data self.left=None self.right=None def inOrder(root): current=root stack=[] while True: if current is not None: stack.append(current) current=current.left elif(stack): current=stack.pop() print(current.data,end="") current=current.right else: break print() root=Node(1) root.left=Node(2) root.right=Node(3) root.left.left=Node(4) root.left.right=Node(5) inOrder(root)
Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!

Outils d'IA chauds

Undresser.AI Undress
Application basée sur l'IA pour créer des photos de nu réalistes

AI Clothes Remover
Outil d'IA en ligne pour supprimer les vêtements des photos.

Undress AI Tool
Images de déshabillage gratuites

Clothoff.io
Dissolvant de vêtements AI

Video Face Swap
Échangez les visages dans n'importe quelle vidéo sans effort grâce à notre outil d'échange de visage AI entièrement gratuit !

Article chaud

Outils chauds

Bloc-notes++7.3.1
Éditeur de code facile à utiliser et gratuit

SublimeText3 version chinoise
Version chinoise, très simple à utiliser

Envoyer Studio 13.0.1
Puissant environnement de développement intégré PHP

Dreamweaver CS6
Outils de développement Web visuel

SublimeText3 version Mac
Logiciel d'édition de code au niveau de Dieu (SublimeText3)

Sujets chauds
 Une analyse approfondie de l'algorithme d'optimisation Grey Wolf (GWO) et de ses forces et faiblesses
Jan 19, 2024 pm 07:48 PM
Une analyse approfondie de l'algorithme d'optimisation Grey Wolf (GWO) et de ses forces et faiblesses
Jan 19, 2024 pm 07:48 PM
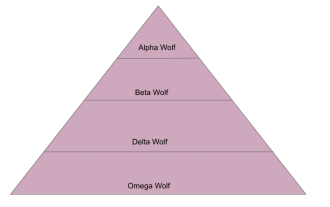
L'algorithme d'optimisation du loup gris (GWO) est un algorithme métaheuristique basé sur la population qui simule la hiérarchie de leadership et le mécanisme de chasse des loups gris dans la nature. Inspiration de l'algorithme du loup gris 1. Les loups gris sont considérés comme des prédateurs au sommet et se situent au sommet de la chaîne alimentaire. 2. Les loups gris aiment vivre en groupe (vivant en groupe), avec une moyenne de 5 à 12 loups dans chaque meute. 3. Les loups gris ont une hiérarchie de dominance sociale très stricte, comme indiqué ci-dessous : Loup alpha : Le loup alpha occupe une position dominante dans l'ensemble du groupe des loups gris et a le droit de commander l'ensemble du groupe des loups gris. Dans l'application des algorithmes, Alpha Wolf est l'une des meilleures solutions, la solution optimale produite par l'algorithme d'optimisation. Loup bêta : Beta wolf rend régulièrement compte à Alpha wolf et aide Alpha wolf à prendre les meilleures décisions. Dans les applications algorithmiques, Beta Wolf peut
 Explorez les principes de base et le processus de mise en œuvre des algorithmes d'échantillonnage imbriqués
Jan 22, 2024 pm 09:51 PM
Explorez les principes de base et le processus de mise en œuvre des algorithmes d'échantillonnage imbriqués
Jan 22, 2024 pm 09:51 PM
L'algorithme d'échantillonnage imbriqué est un algorithme d'inférence statistique bayésien efficace utilisé pour calculer l'intégrale ou la sommation sous des distributions de probabilité complexes. Il fonctionne en décomposant l'espace des paramètres en plusieurs hypercubes de volume égal, et en « poussant » progressivement et itérativement l'un des hypercubes de plus petit volume, puis en remplissant l'hypercube avec des échantillons aléatoires pour mieux estimer la valeur intégrale de la distribution de probabilité. Grâce à une itération continue, l'algorithme d'échantillonnage imbriqué peut obtenir des valeurs intégrales et des limites de l'espace des paramètres de haute précision, qui peuvent être appliquées à des problèmes statistiques tels que la comparaison de modèles, l'estimation des paramètres et la sélection de modèles. L'idée principale de cet algorithme est de transformer des problèmes d'intégration complexes en une série de problèmes d'intégration simples et d'approcher la véritable valeur intégrale en réduisant progressivement le volume de l'espace des paramètres. Chaque étape d'itération échantillonne aléatoirement dans l'espace des paramètres
 Explication détaillée de l'algorithme Bellman Ford et de sa mise en œuvre en Python
Jan 22, 2024 pm 07:39 PM
Explication détaillée de l'algorithme Bellman Ford et de sa mise en œuvre en Python
Jan 22, 2024 pm 07:39 PM
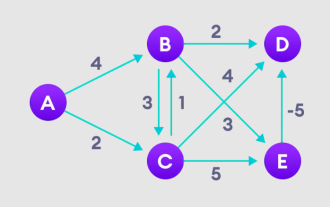
L'algorithme Bellman Ford peut trouver le chemin le plus court entre le nœud cible et les autres nœuds du graphique pondéré. Ceci est très similaire à l'algorithme de Dijkstra. L'algorithme de Bellman-Ford peut gérer des graphiques avec des poids négatifs et est relativement simple en termes de mise en œuvre. Explication détaillée du principe de l'algorithme de Bellman Ford L'algorithme de Bellman Ford trouve de manière itérative de nouveaux chemins plus courts que les chemins surestimés en surestimant les longueurs de chemin depuis le sommet de départ jusqu'à tous les autres sommets. Parce que nous voulons enregistrer la distance du trajet de chaque nœud, nous pouvons la stocker dans un tableau de taille n, où n représente également le nombre de nœuds. Exemple Figure 1. Sélectionnez le nœud de départ, attribuez-le à tous les autres sommets à l'infini et enregistrez la valeur du chemin. 2. Visitez chaque bord et effectuez des opérations de relaxation pour mettre à jour en permanence le chemin le plus court. 3. Nous avons besoin
 Introduction à l'algorithme Wu-Manber et aux instructions d'implémentation Python
Jan 23, 2024 pm 07:03 PM
Introduction à l'algorithme Wu-Manber et aux instructions d'implémentation Python
Jan 23, 2024 pm 07:03 PM
L'algorithme Wu-Manber est un algorithme de correspondance de chaînes utilisé pour rechercher efficacement des chaînes. Il s'agit d'un algorithme hybride qui combine les avantages des algorithmes de Boyer-Moore et de Knuth-Morris-Pratt pour fournir une correspondance de modèles rapide et précise. Étape 1 de l'algorithme Wu-Manber. Créez une table de hachage qui mappe chaque sous-chaîne possible du modèle à la position du modèle où cette sous-chaîne apparaît. 2. Cette table de hachage est utilisée pour identifier rapidement les emplacements de départ potentiels des modèles dans le texte. 3. Parcourez le texte et comparez chaque caractère au caractère correspondant dans le modèle. 4. Si les caractères correspondent, vous pouvez passer au caractère suivant et poursuivre la comparaison. 5. Si les caractères ne correspondent pas, vous pouvez utiliser une table de hachage pour déterminer le prochain caractère potentiel du modèle.
 Quel est le rôle du gain d'information dans l'algorithme id3 ?
Jan 23, 2024 pm 11:27 PM
Quel est le rôle du gain d'information dans l'algorithme id3 ?
Jan 23, 2024 pm 11:27 PM
L'algorithme ID3 est l'un des algorithmes de base de l'apprentissage des arbres de décision. Il sélectionne le meilleur point de partage en calculant le gain d'informations de chaque fonctionnalité pour générer un arbre de décision. Le gain d'informations est un concept important dans l'algorithme ID3, utilisé pour mesurer la contribution des caractéristiques à la tâche de classification. Cet article présentera en détail le concept, la méthode de calcul et l'application du gain d'information dans l'algorithme ID3. 1. Le concept d'entropie de l'information L'entropie de l'information est un concept de la théorie de l'information qui mesure l'incertitude des variables aléatoires. Pour un nombre de variable aléatoire discrète, et p(x_i) représente la probabilité que la variable aléatoire X prenne la valeur x_i. lettre
 Analyser les principes, les modèles et la composition de l'algorithme de recherche Sparrow (SSA)
Jan 19, 2024 pm 10:27 PM
Analyser les principes, les modèles et la composition de l'algorithme de recherche Sparrow (SSA)
Jan 19, 2024 pm 10:27 PM
L'algorithme de recherche Sparrow (SSA) est un algorithme d'optimisation méta-heuristique basé sur le comportement anti-prédation et de recherche de nourriture des moineaux. Le comportement alimentaire des moineaux peut être divisé en deux types principaux : les producteurs et les charognards. Les producteurs recherchent activement de la nourriture, tandis que les charognards rivalisent pour obtenir de la nourriture auprès des producteurs. Principe de l'algorithme de recherche de moineau (SSA) Dans l'algorithme de recherche de moineau (SSA), chaque moineau porte une attention particulière au comportement de ses voisins. En employant différentes stratégies de recherche de nourriture, les individus sont capables d’utiliser efficacement l’énergie retenue pour rechercher davantage de nourriture. De plus, les oiseaux sont plus vulnérables aux prédateurs dans leur espace de recherche et doivent donc trouver des endroits plus sûrs. Les oiseaux au centre d’une colonie peuvent minimiser leur propre danger en restant proches de leurs voisins. Lorsqu'un oiseau repère un prédateur, il émet un cri d'alarme
 Principes d'optimisation numérique et analyse de l'algorithme d'optimisation des baleines (WOA)
Jan 19, 2024 pm 07:27 PM
Principes d'optimisation numérique et analyse de l'algorithme d'optimisation des baleines (WOA)
Jan 19, 2024 pm 07:27 PM
L'algorithme d'optimisation des baleines (WOA) est un algorithme d'optimisation métaheuristique inspiré de la nature qui simule le comportement de chasse des baleines à bosse et est utilisé pour l'optimisation de problèmes numériques. L'algorithme d'optimisation Whale (WOA) commence avec un ensemble de solutions aléatoires et optimise en fonction d'un agent de recherche sélectionné au hasard ou de la meilleure solution jusqu'à présent grâce à des mises à jour de position de l'agent de recherche à chaque itération. Inspiration de l'algorithme d'optimisation des baleines L'algorithme d'optimisation des baleines s'inspire du comportement de chasse des baleines à bosse. Les baleines à bosse préfèrent la nourriture trouvée près de la surface, comme le krill et les bancs de poissons. Par conséquent, les baleines à bosse rassemblent de la nourriture pour former un réseau de bulles en soufflant des bulles dans une spirale ascendante lorsqu’elles chassent. Dans une manœuvre de « spirale ascendante », la baleine à bosse plonge à environ 12 m, puis commence à former une bulle en spirale autour de sa proie et nage vers le haut.
 Algorithme SIFT (Scale Invariant Features)
Jan 22, 2024 pm 05:09 PM
Algorithme SIFT (Scale Invariant Features)
Jan 22, 2024 pm 05:09 PM
L'algorithme SIFT (Scale Invariant Feature Transform) est un algorithme d'extraction de caractéristiques utilisé dans les domaines du traitement d'images et de la vision par ordinateur. Cet algorithme a été proposé en 1999 pour améliorer les performances de reconnaissance et de correspondance d'objets dans les systèmes de vision par ordinateur. L'algorithme SIFT est robuste et précis et est largement utilisé dans la reconnaissance d'images, la reconstruction tridimensionnelle, la détection de cibles, le suivi vidéo et d'autres domaines. Il obtient l'invariance d'échelle en détectant les points clés dans plusieurs espaces d'échelle et en extrayant des descripteurs de caractéristiques locales autour des points clés. Les principales étapes de l'algorithme SIFT comprennent la construction d'un espace d'échelle, la détection des points clés, le positionnement des points clés, l'attribution de directions et la génération de descripteurs de caractéristiques. Grâce à ces étapes, l’algorithme SIFT peut extraire des fonctionnalités robustes et uniques, permettant ainsi un traitement d’image efficace.





