Différences et connexions : AIC et bBIC

AIC (Akaike Information Criterion) et BIC (Bayesian Information Criterion) sont des critères de sélection de modèles couramment utilisés pour comparer différents modèles et sélectionner le modèle qui correspond le mieux aux données. L'objectif des deux critères est de trouver un équilibre entre la qualité de l'ajustement et la complexité du modèle afin d'éviter les problèmes de surajustement ou de sous-ajustement. L'AIC a été proposé par Hirotugu Akaike. Il est basé sur le concept de théorie de l'information et considère l'équilibre entre la qualité de l'ajustement du modèle et le nombre de paramètres. La formule de calcul de l'AIC est AIC = -2log(L) + 2k, où L représente l'estimation du maximum de vraisemblance du modèle et k représente le nombre de paramètres du modèle. BIC a été proposé par Gideon E. Schwarz et est basé sur le bayésien
AIC et BIC sont des indicateurs utilisés pour évaluer l'adéquation et la complexité du modèle et peuvent être appliqués à divers modèles statistiques, y compris les méthodes de clustering. Cependant, les formes spécifiques d'AIC et de BIC peuvent différer en raison des différents types de méthodes de regroupement et d'hypothèses concernant la distribution des données.
La principale différence entre AIC et BIC réside dans la manière dont ils évaluent le compromis entre l'adéquation et la complexité.
AIC est basé sur le principe du maximum de vraisemblance, qui pénalise les modèles comportant un grand nombre de paramètres relatifs à la taille des données.
La formule AIC
AIC=2k-2ln(L)
L'objectif est de trouver le modèle avec la valeur AIC la plus basse pour équilibrer la qualité de l'ajustement et la complexité. où k est le nombre de paramètres du modèle, qui est la vraisemblance maximale du modèle L.
BIC est similaire à AIC, mais il pénalise plus sévèrement les modèles avec un plus grand nombre de paramètres.
La formule de BIC
BIC=kln(n)-2ln(L)
où k est le nombre n de paramètres du modèle, le nombre de points de données et L est la vraisemblance maximale du modèle. L’objectif est de trouver le modèle avec la valeur BIC la plus basse, car cela indique que le modèle présente le meilleur équilibre entre qualité d’ajustement et complexité.
En général, BIC pénalisera plus sévèrement les modèles avec un grand nombre de paramètres que l'AIC, BIC peut donc être utilisé lorsque l'objectif est de trouver un modèle plus parcimonieux.
Dans le contexte de la sélection de modèles, un modèle parcimonieux est un modèle qui a un petit nombre de paramètres mais qui s'adapte toujours bien aux données. L'objectif des modèles parcimonieux est de simplifier le modèle et de réduire la complexité tout en capturant les caractéristiques essentielles des données. Lorsqu’ils fournissent des niveaux de précision similaires, les modèles parcimonieux sont préférés aux modèles plus complexes car ils sont plus faciles à interpréter, moins sujets au surajustement et plus efficaces en termes de calcul.
Notez également que AIC et BIC peuvent être utilisés pour comparer différents modèles et sélectionner le meilleur modèle pour un ensemble de données donné.
Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!

Outils d'IA chauds

Undresser.AI Undress
Application basée sur l'IA pour créer des photos de nu réalistes

AI Clothes Remover
Outil d'IA en ligne pour supprimer les vêtements des photos.

Undress AI Tool
Images de déshabillage gratuites

Clothoff.io
Dissolvant de vêtements AI

AI Hentai Generator
Générez AI Hentai gratuitement.

Article chaud

Outils chauds

Bloc-notes++7.3.1
Éditeur de code facile à utiliser et gratuit

SublimeText3 version chinoise
Version chinoise, très simple à utiliser

Envoyer Studio 13.0.1
Puissant environnement de développement intégré PHP

Dreamweaver CS6
Outils de développement Web visuel

SublimeText3 version Mac
Logiciel d'édition de code au niveau de Dieu (SublimeText3)
 Bytedance Cutting lance le super abonnement SVIP : 499 yuans pour un abonnement annuel continu, offrant une variété de fonctions d'IA
Jun 28, 2024 am 03:51 AM
Bytedance Cutting lance le super abonnement SVIP : 499 yuans pour un abonnement annuel continu, offrant une variété de fonctions d'IA
Jun 28, 2024 am 03:51 AM
Ce site a rapporté le 27 juin que Jianying est un logiciel de montage vidéo développé par FaceMeng Technology, une filiale de ByteDance. Il s'appuie sur la plateforme Douyin et produit essentiellement du contenu vidéo court pour les utilisateurs de la plateforme. Il est compatible avec iOS, Android et. Windows, MacOS et autres systèmes d'exploitation. Jianying a officiellement annoncé la mise à niveau de son système d'adhésion et a lancé un nouveau SVIP, qui comprend une variété de technologies noires d'IA, telles que la traduction intelligente, la mise en évidence intelligente, l'emballage intelligent, la synthèse humaine numérique, etc. En termes de prix, les frais mensuels pour le clipping SVIP sont de 79 yuans, les frais annuels sont de 599 yuans (attention sur ce site : équivalent à 49,9 yuans par mois), l'abonnement mensuel continu est de 59 yuans par mois et l'abonnement annuel continu est de 59 yuans par mois. est de 499 yuans par an (équivalent à 41,6 yuans par mois) . En outre, le responsable de Cut a également déclaré que afin d'améliorer l'expérience utilisateur, ceux qui se sont abonnés au VIP d'origine
 Assistant de codage d'IA augmenté par le contexte utilisant Rag et Sem-Rag
Jun 10, 2024 am 11:08 AM
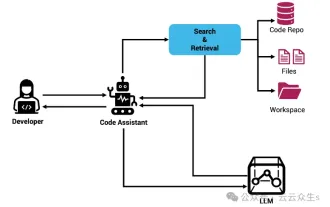
Assistant de codage d'IA augmenté par le contexte utilisant Rag et Sem-Rag
Jun 10, 2024 am 11:08 AM
Améliorez la productivité, l’efficacité et la précision des développeurs en intégrant une génération et une mémoire sémantique améliorées par la récupération dans les assistants de codage IA. Traduit de EnhancingAICodingAssistantswithContextUsingRAGandSEM-RAG, auteur JanakiramMSV. Bien que les assistants de programmation d'IA de base soient naturellement utiles, ils ne parviennent souvent pas à fournir les suggestions de code les plus pertinentes et les plus correctes, car ils s'appuient sur une compréhension générale du langage logiciel et des modèles d'écriture de logiciels les plus courants. Le code généré par ces assistants de codage est adapté à la résolution des problèmes qu’ils sont chargés de résoudre, mais n’est souvent pas conforme aux normes, conventions et styles de codage des équipes individuelles. Cela aboutit souvent à des suggestions qui doivent être modifiées ou affinées pour que le code soit accepté dans l'application.
 Sept questions d'entretien technique Cool GenAI et LLM
Jun 07, 2024 am 10:06 AM
Sept questions d'entretien technique Cool GenAI et LLM
Jun 07, 2024 am 10:06 AM
Pour en savoir plus sur l'AIGC, veuillez visiter : 51CTOAI.x Community https://www.51cto.com/aigc/Translator|Jingyan Reviewer|Chonglou est différent de la banque de questions traditionnelle que l'on peut voir partout sur Internet. nécessite de sortir des sentiers battus. Les grands modèles linguistiques (LLM) sont de plus en plus importants dans les domaines de la science des données, de l'intelligence artificielle générative (GenAI) et de l'intelligence artificielle. Ces algorithmes complexes améliorent les compétences humaines et stimulent l’efficacité et l’innovation dans de nombreux secteurs, devenant ainsi la clé permettant aux entreprises de rester compétitives. LLM a un large éventail d'applications. Il peut être utilisé dans des domaines tels que le traitement du langage naturel, la génération de texte, la reconnaissance vocale et les systèmes de recommandation. En apprenant de grandes quantités de données, LLM est capable de générer du texte
 Le réglage fin peut-il vraiment permettre au LLM d'apprendre de nouvelles choses : l'introduction de nouvelles connaissances peut amener le modèle à produire davantage d'hallucinations
Jun 11, 2024 pm 03:57 PM
Le réglage fin peut-il vraiment permettre au LLM d'apprendre de nouvelles choses : l'introduction de nouvelles connaissances peut amener le modèle à produire davantage d'hallucinations
Jun 11, 2024 pm 03:57 PM
Les grands modèles linguistiques (LLM) sont formés sur d'énormes bases de données textuelles, où ils acquièrent de grandes quantités de connaissances du monde réel. Ces connaissances sont intégrées à leurs paramètres et peuvent ensuite être utilisées en cas de besoin. La connaissance de ces modèles est « réifiée » en fin de formation. À la fin de la pré-formation, le modèle arrête effectivement d’apprendre. Alignez ou affinez le modèle pour apprendre à exploiter ces connaissances et répondre plus naturellement aux questions des utilisateurs. Mais parfois, la connaissance du modèle ne suffit pas, et bien que le modèle puisse accéder à du contenu externe via RAG, il est considéré comme bénéfique de l'adapter à de nouveaux domaines grâce à un réglage fin. Ce réglage fin est effectué à l'aide de la contribution d'annotateurs humains ou d'autres créations LLM, où le modèle rencontre des connaissances supplémentaires du monde réel et les intègre.
 Afin de fournir un nouveau système de référence et d'évaluation de questions-réponses scientifiques et complexes pour les grands modèles, l'UNSW, Argonne, l'Université de Chicago et d'autres institutions ont lancé conjointement le cadre SciQAG.
Jul 25, 2024 am 06:42 AM
Afin de fournir un nouveau système de référence et d'évaluation de questions-réponses scientifiques et complexes pour les grands modèles, l'UNSW, Argonne, l'Université de Chicago et d'autres institutions ont lancé conjointement le cadre SciQAG.
Jul 25, 2024 am 06:42 AM
L'ensemble de données ScienceAI Question Answering (QA) joue un rôle essentiel dans la promotion de la recherche sur le traitement du langage naturel (NLP). Des ensembles de données d'assurance qualité de haute qualité peuvent non seulement être utilisés pour affiner les modèles, mais également évaluer efficacement les capacités des grands modèles linguistiques (LLM), en particulier la capacité à comprendre et à raisonner sur les connaissances scientifiques. Bien qu’il existe actuellement de nombreux ensembles de données scientifiques d’assurance qualité couvrant la médecine, la chimie, la biologie et d’autres domaines, ces ensembles de données présentent encore certaines lacunes. Premièrement, le formulaire de données est relativement simple, et la plupart sont des questions à choix multiples. Elles sont faciles à évaluer, mais limitent la plage de sélection des réponses du modèle et ne peuvent pas tester pleinement la capacité du modèle à répondre aux questions scientifiques. En revanche, les questions et réponses ouvertes
 Cinq écoles d'apprentissage automatique que vous ne connaissez pas
Jun 05, 2024 pm 08:51 PM
Cinq écoles d'apprentissage automatique que vous ne connaissez pas
Jun 05, 2024 pm 08:51 PM
L'apprentissage automatique est une branche importante de l'intelligence artificielle qui donne aux ordinateurs la possibilité d'apprendre à partir de données et d'améliorer leurs capacités sans être explicitement programmés. L'apprentissage automatique a un large éventail d'applications dans divers domaines, de la reconnaissance d'images et du traitement du langage naturel aux systèmes de recommandation et à la détection des fraudes, et il change notre façon de vivre. Il existe de nombreuses méthodes et théories différentes dans le domaine de l'apprentissage automatique, parmi lesquelles les cinq méthodes les plus influentes sont appelées les « Cinq écoles d'apprentissage automatique ». Les cinq grandes écoles sont l’école symbolique, l’école connexionniste, l’école évolutionniste, l’école bayésienne et l’école analogique. 1. Le symbolisme, également connu sous le nom de symbolisme, met l'accent sur l'utilisation de symboles pour le raisonnement logique et l'expression des connaissances. Cette école de pensée estime que l'apprentissage est un processus de déduction inversée, à travers les connaissances existantes.
 Les performances de SOTA, la méthode d'IA de prédiction d'affinité protéine-ligand multimodale de Xiamen, combinent pour la première fois des informations sur la surface moléculaire
Jul 17, 2024 pm 06:37 PM
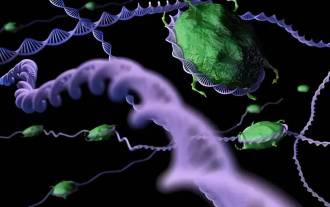
Les performances de SOTA, la méthode d'IA de prédiction d'affinité protéine-ligand multimodale de Xiamen, combinent pour la première fois des informations sur la surface moléculaire
Jul 17, 2024 pm 06:37 PM
Editeur | KX Dans le domaine de la recherche et du développement de médicaments, il est crucial de prédire avec précision et efficacité l'affinité de liaison des protéines et des ligands pour le criblage et l'optimisation des médicaments. Cependant, les études actuelles ne prennent pas en compte le rôle important des informations sur la surface moléculaire dans les interactions protéine-ligand. Sur cette base, des chercheurs de l'Université de Xiamen ont proposé un nouveau cadre d'extraction de caractéristiques multimodales (MFE), qui combine pour la première fois des informations sur la surface des protéines, la structure et la séquence 3D, et utilise un mécanisme d'attention croisée pour comparer différentes modalités. alignement. Les résultats expérimentaux démontrent que cette méthode atteint des performances de pointe dans la prédiction des affinités de liaison protéine-ligand. De plus, les études d’ablation démontrent l’efficacité et la nécessité des informations sur la surface des protéines et de l’alignement des caractéristiques multimodales dans ce cadre. Les recherches connexes commencent par "S
 Préparant des marchés tels que l'IA, GlobalFoundries acquiert la technologie du nitrure de gallium de Tagore Technology et les équipes associées
Jul 15, 2024 pm 12:21 PM
Préparant des marchés tels que l'IA, GlobalFoundries acquiert la technologie du nitrure de gallium de Tagore Technology et les équipes associées
Jul 15, 2024 pm 12:21 PM
Selon les informations de ce site Web du 5 juillet, GlobalFoundries a publié un communiqué de presse le 1er juillet de cette année, annonçant l'acquisition de la technologie de nitrure de gallium (GaN) et du portefeuille de propriété intellectuelle de Tagore Technology, dans l'espoir d'élargir sa part de marché dans l'automobile et Internet. des objets et des domaines d'application des centres de données d'intelligence artificielle pour explorer une efficacité plus élevée et de meilleures performances. Alors que des technologies telles que l’intelligence artificielle générative (GenerativeAI) continuent de se développer dans le monde numérique, le nitrure de gallium (GaN) est devenu une solution clé pour une gestion durable et efficace de l’énergie, notamment dans les centres de données. Ce site Web citait l'annonce officielle selon laquelle, lors de cette acquisition, l'équipe d'ingénierie de Tagore Technology rejoindrait GF pour développer davantage la technologie du nitrure de gallium. g






