 Périphériques technologiques
Périphériques technologiques
 IA
IA
 Le réseau neuronal monocouche ne peut pas résoudre la cause première du problème XOR
Le réseau neuronal monocouche ne peut pas résoudre la cause première du problème XOR
Le réseau neuronal monocouche ne peut pas résoudre la cause première du problème XOR

Dans le domaine de l'apprentissage automatique, le réseau de neurones est un modèle important qui fonctionne bien dans de nombreuses tâches. Cependant, certaines tâches sont difficiles à résoudre pour les réseaux neuronaux monocouches. Un exemple typique est le problème XOR. Le problème XOR signifie que pour l’entrée de deux nombres binaires, le résultat de sortie est 1 si et seulement si les deux entrées ne sont pas identiques. Cet article expliquera les raisons pour lesquelles un réseau neuronal monocouche ne peut pas résoudre le problème XOR sous trois aspects : les caractéristiques structurelles du réseau neuronal monocouche, les caractéristiques essentielles du problème XOR et le processus de formation du réseau neuronal.
Tout d'abord, les caractéristiques structurelles d'un réseau neuronal monocouche déterminent qu'il ne peut pas résoudre le problème XOR. Un réseau neuronal monocouche se compose d’une couche d’entrée, d’une couche de sortie et d’une fonction d’activation. Il n'y a pas d'autres couches entre la couche d'entrée et la couche de sortie, ce qui signifie qu'un réseau neuronal monocouche ne peut réaliser qu'une classification linéaire. La classification linéaire fait référence à une méthode de classification qui peut utiliser une ligne droite pour séparer les points de données en deux catégories. Cependant, le problème XOR est un problème de classification non linéaire et ne peut donc pas être résolu par un réseau neuronal monocouche. En effet, les points de données du problème XOR ne peuvent pas être parfaitement divisés par une ligne droite. Pour le problème XOR, nous devons introduire des réseaux de neurones multicouches, également appelés réseaux de neurones profonds, pour résoudre les problèmes de classification non linéaire. Les réseaux neuronaux multicouches comportent plusieurs couches cachées, et chaque couche cachée peut apprendre et extraire différentes fonctionnalités pour mieux résoudre des problèmes de classification complexes. En introduisant des couches cachées, les réseaux de neurones peuvent apprendre des combinaisons de fonctionnalités plus complexes et approcher la limite de décision du problème XOR via plusieurs transformations non linéaires. De cette manière, les réseaux neuronaux multicouches peuvent mieux résoudre les problèmes de classification non linéaire, y compris les problèmes XOR. Dans l'ensemble, la caractéristique essentielle du problème
XOR linéaire d'un réseau neuronal monocouche est que les points de données ne peuvent pas être parfaitement divisés en deux catégories par une ligne droite. C'est une raison importante pour laquelle un réseau neuronal monocouche ne peut pas. résoudre ce problème. En prenant comme exemple la représentation des points de données sur un plan, les points bleus représentent des points de données avec un résultat de sortie de 0 et les points rouges représentent des points de données avec un résultat de sortie de 1. On peut observer que ces points de données ne peuvent pas être parfaitement divisés en deux catégories par une ligne droite et ne peuvent donc pas être classés avec un réseau neuronal à une seule couche. Le processus
est le facteur clé qui affecte le réseau neuronal monocouche pour résoudre le problème XOR. La formation des réseaux de neurones utilise généralement l'algorithme de rétropropagation, basé sur la méthode d'optimisation de la descente de gradient. Cependant, dans un réseau neuronal monocouche, l’algorithme de descente de gradient ne peut trouver que la solution optimale locale et ne peut pas trouver la solution optimale globale. En effet, les caractéristiques du problème XOR font que sa fonction de perte n'est pas convexe. Il existe plusieurs solutions optimales locales dans le processus d'optimisation des fonctions non convexes, ce qui empêche le réseau neuronal monocouche de trouver la solution optimale globale.
Il y a trois raisons principales pour lesquelles un réseau neuronal monocouche ne peut pas résoudre le problème XOR. Tout d’abord, les caractéristiques structurelles d’un réseau neuronal monocouche déterminent qu’il ne peut réaliser qu’une classification linéaire. Puisque la caractéristique essentielle du problème XOR est un problème de classification non linéaire, un réseau neuronal monocouche ne peut pas le classer avec précision. Deuxièmement, la distribution des données du problème XOR n'est pas linéairement séparable, ce qui signifie que les deux types de données ne peuvent pas être complètement séparés par une ligne droite. Par conséquent, un réseau neuronal monocouche ne peut pas permettre la classification des problèmes XOR par une simple transformation linéaire. Enfin, il peut y avoir plusieurs solutions optimales locales pendant le processus de formation du réseau neuronal, et la solution optimale globale ne peut pas être trouvée. En effet, l'espace des paramètres d'un réseau neuronal monocouche n'est pas convexe et il existe plusieurs solutions optimales locales. Il est donc difficile de trouver la solution optimale globale à l'aide d'un simple algorithme de descente de gradient. Par conséquent, un réseau neuronal monocouche ne peut pas résoudre le problème XOR.
Par conséquent, afin de résoudre le problème XOR, des réseaux de neurones multicouches ou d'autres modèles plus complexes doivent être utilisés. Les réseaux neuronaux multicouches peuvent réaliser une classification non linéaire en introduisant des couches cachées, et peuvent également utiliser des algorithmes d'optimisation plus complexes pour trouver la solution optimale globale.
Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!

Outils d'IA chauds

Undresser.AI Undress
Application basée sur l'IA pour créer des photos de nu réalistes

AI Clothes Remover
Outil d'IA en ligne pour supprimer les vêtements des photos.

Undress AI Tool
Images de déshabillage gratuites

Clothoff.io
Dissolvant de vêtements AI

Video Face Swap
Échangez les visages dans n'importe quelle vidéo sans effort grâce à notre outil d'échange de visage AI entièrement gratuit !

Article chaud

Outils chauds

Bloc-notes++7.3.1
Éditeur de code facile à utiliser et gratuit

SublimeText3 version chinoise
Version chinoise, très simple à utiliser

Envoyer Studio 13.0.1
Puissant environnement de développement intégré PHP

Dreamweaver CS6
Outils de développement Web visuel

SublimeText3 version Mac
Logiciel d'édition de code au niveau de Dieu (SublimeText3)
 Explorez les concepts, les différences, les avantages et les inconvénients de RNN, LSTM et GRU
Jan 22, 2024 pm 07:51 PM
Explorez les concepts, les différences, les avantages et les inconvénients de RNN, LSTM et GRU
Jan 22, 2024 pm 07:51 PM
Dans les données de séries chronologiques, il existe des dépendances entre les observations, elles ne sont donc pas indépendantes les unes des autres. Cependant, les réseaux de neurones traditionnels traitent chaque observation comme indépendante, ce qui limite la capacité du modèle à modéliser des données de séries chronologiques. Pour résoudre ce problème, le réseau neuronal récurrent (RNN) a été introduit, qui a introduit le concept de mémoire pour capturer les caractéristiques dynamiques des données de séries chronologiques en établissant des dépendances entre les points de données du réseau. Grâce à des connexions récurrentes, RNN peut transmettre des informations antérieures à l'observation actuelle pour mieux prédire les valeurs futures. Cela fait de RNN un outil puissant pour les tâches impliquant des données de séries chronologiques. Mais comment RNN parvient-il à obtenir ce type de mémoire ? RNN réalise la mémoire via la boucle de rétroaction dans le réseau neuronal. C'est la différence entre RNN et le réseau neuronal traditionnel.
 Une étude de cas sur l'utilisation du modèle LSTM bidirectionnel pour la classification de texte
Jan 24, 2024 am 10:36 AM
Une étude de cas sur l'utilisation du modèle LSTM bidirectionnel pour la classification de texte
Jan 24, 2024 am 10:36 AM
Le modèle LSTM bidirectionnel est un réseau neuronal utilisé pour la classification de texte. Vous trouverez ci-dessous un exemple simple montrant comment utiliser le LSTM bidirectionnel pour les tâches de classification de texte. Tout d'abord, nous devons importer les bibliothèques et modules requis : importosimportnumpyasnpfromkeras.preprocessing.textimportTokenizerfromkeras.preprocessing.sequenceimportpad_sequencesfromkeras.modelsimportSequentialfromkeras.layersimportDense,Em
 Calcul des opérandes à virgule flottante (FLOPS) pour les réseaux de neurones
Jan 22, 2024 pm 07:21 PM
Calcul des opérandes à virgule flottante (FLOPS) pour les réseaux de neurones
Jan 22, 2024 pm 07:21 PM
FLOPS est l'une des normes d'évaluation des performances informatiques, utilisée pour mesurer le nombre d'opérations en virgule flottante par seconde. Dans les réseaux de neurones, FLOPS est souvent utilisé pour évaluer la complexité informatique du modèle et l'utilisation des ressources informatiques. C'est un indicateur important utilisé pour mesurer la puissance de calcul et l'efficacité d'un ordinateur. Un réseau de neurones est un modèle complexe composé de plusieurs couches de neurones utilisées pour des tâches telles que la classification, la régression et le clustering des données. La formation et l'inférence des réseaux de neurones nécessitent un grand nombre de multiplications matricielles, de convolutions et d'autres opérations de calcul, la complexité de calcul est donc très élevée. FLOPS (FloatingPointOperationsperSecond) peut être utilisé pour mesurer la complexité de calcul des réseaux de neurones afin d'évaluer l'efficacité d'utilisation des ressources de calcul du modèle. FIASCO
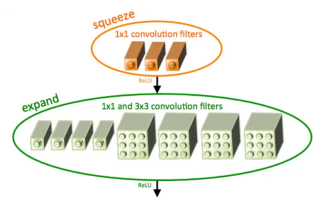 Introduction à SqueezeNet et ses caractéristiques
Jan 22, 2024 pm 07:15 PM
Introduction à SqueezeNet et ses caractéristiques
Jan 22, 2024 pm 07:15 PM
SqueezeNet est un algorithme petit et précis qui établit un bon équilibre entre haute précision et faible complexité, ce qui le rend idéal pour les systèmes mobiles et embarqués aux ressources limitées. En 2016, des chercheurs de DeepScale, de l'Université de Californie à Berkeley et de l'Université de Stanford ont proposé SqueezeNet, un réseau neuronal convolutif (CNN) compact et efficace. Ces dernières années, les chercheurs ont apporté plusieurs améliorations à SqueezeNet, notamment SqueezeNetv1.1 et SqueezeNetv2.0. Les améliorations apportées aux deux versions augmentent non seulement la précision, mais réduisent également les coûts de calcul. Précision de SqueezeNetv1.1 sur l'ensemble de données ImageNet
 Définition et analyse structurelle du réseau neuronal flou
Jan 22, 2024 pm 09:09 PM
Définition et analyse structurelle du réseau neuronal flou
Jan 22, 2024 pm 09:09 PM
Le réseau de neurones flous est un modèle hybride qui combine la logique floue et les réseaux de neurones pour résoudre des problèmes flous ou incertains difficiles à gérer avec les réseaux de neurones traditionnels. Sa conception s'inspire du flou et de l'incertitude de la cognition humaine, c'est pourquoi il est largement utilisé dans les systèmes de contrôle, la reconnaissance de formes, l'exploration de données et d'autres domaines. L'architecture de base du réseau neuronal flou se compose d'un sous-système flou et d'un sous-système neuronal. Le sous-système flou utilise la logique floue pour traiter les données d'entrée et les convertir en ensembles flous pour exprimer le flou et l'incertitude des données d'entrée. Le sous-système neuronal utilise des réseaux de neurones pour traiter des ensembles flous pour des tâches telles que la classification, la régression ou le clustering. L'interaction entre le sous-système flou et le sous-système neuronal confère au réseau neuronal flou des capacités de traitement plus puissantes et peut
 Débruitage d'image à l'aide de réseaux de neurones convolutifs
Jan 23, 2024 pm 11:48 PM
Débruitage d'image à l'aide de réseaux de neurones convolutifs
Jan 23, 2024 pm 11:48 PM
Les réseaux de neurones convolutifs fonctionnent bien dans les tâches de débruitage d'images. Il utilise les filtres appris pour filtrer le bruit et restaurer ainsi l'image originale. Cet article présente en détail la méthode de débruitage d'image basée sur un réseau neuronal convolutif. 1. Présentation du réseau neuronal convolutif Le réseau neuronal convolutif est un algorithme d'apprentissage en profondeur qui utilise une combinaison de plusieurs couches convolutives, des couches de regroupement et des couches entièrement connectées pour apprendre et classer les caractéristiques de l'image. Dans la couche convolutive, les caractéristiques locales de l'image sont extraites via des opérations de convolution, capturant ainsi la corrélation spatiale dans l'image. La couche de pooling réduit la quantité de calcul en réduisant la dimension des fonctionnalités et conserve les principales fonctionnalités. La couche entièrement connectée est responsable du mappage des fonctionnalités et des étiquettes apprises pour mettre en œuvre la classification des images ou d'autres tâches. La conception de cette structure de réseau rend les réseaux de neurones convolutifs utiles dans le traitement et la reconnaissance d'images.
 Comparez les similitudes, les différences et les relations entre la convolution dilatée et la convolution atreuse
Jan 22, 2024 pm 10:27 PM
Comparez les similitudes, les différences et les relations entre la convolution dilatée et la convolution atreuse
Jan 22, 2024 pm 10:27 PM
La convolution dilatée et la convolution dilatée sont des opérations couramment utilisées dans les réseaux de neurones convolutifs. Cet article présentera en détail leurs différences et leurs relations. 1. Convolution dilatée La convolution dilatée, également connue sous le nom de convolution dilatée ou convolution dilatée, est une opération dans un réseau neuronal convolutif. Il s'agit d'une extension basée sur l'opération de convolution traditionnelle et augmente le champ récepteur du noyau de convolution en insérant des trous dans le noyau de convolution. De cette façon, le réseau peut mieux capturer un plus large éventail de fonctionnalités. La convolution dilatée est largement utilisée dans le domaine du traitement d'images et peut améliorer les performances du réseau sans augmenter le nombre de paramètres ni la quantité de calcul. En élargissant le champ de réception du noyau de convolution, la convolution dilatée peut mieux traiter les informations globales dans l'image, améliorant ainsi l'effet d'extraction de caractéristiques. L'idée principale de la convolution dilatée est d'introduire quelques
 Étapes pour écrire un réseau neuronal simple à l'aide de Rust
Jan 23, 2024 am 10:45 AM
Étapes pour écrire un réseau neuronal simple à l'aide de Rust
Jan 23, 2024 am 10:45 AM
Rust est un langage de programmation au niveau système axé sur la sécurité, les performances et la concurrence. Il vise à fournir un langage de programmation sûr et fiable adapté à des scénarios tels que les systèmes d'exploitation, les applications réseau et les systèmes embarqués. La sécurité de Rust vient principalement de deux aspects : le système de propriété et le vérificateur d'emprunt. Le système de propriété permet au compilateur de vérifier le code pour détecter les erreurs de mémoire au moment de la compilation, évitant ainsi les problèmes courants de sécurité de la mémoire. En forçant la vérification des transferts de propriété des variables au moment de la compilation, Rust garantit que les ressources mémoire sont correctement gérées et libérées. Le vérificateur d'emprunt analyse le cycle de vie de la variable pour garantir que la même variable ne sera pas accédée par plusieurs threads en même temps, évitant ainsi les problèmes de sécurité de concurrence courants. En combinant ces deux mécanismes, Rust est capable de fournir





