Pourquoi diviser 8 par -3 en PHP donne-t-il 0 ?

Pourquoi PHP8%-3 est-il égal à 0 ?
En programmation PHP, nous rencontrons parfois des problèmes étranges et déroutants. Une question particulièrement intéressante est la suivante : pourquoi l’expression 8%-3 en PHP est-elle égale à 0 ?
Pour répondre à cette question, nous devons d'abord comprendre l'opération modulaire (opération restante) en PHP. L'arithmétique modulo est une opération mathématique utilisée pour calculer le reste après avoir divisé un nombre par un autre. En PHP, le signe pourcentage (%) est utilisé pour représenter l'arithmétique modulaire.
En mathématiques, lorsque le reste de la division d'un nombre par un autre nombre est 0, on dit que les deux nombres sont divisibles. En d’autres termes, si un nombre est divisible par un autre nombre, le résultat de l’opération modulo entre eux sera 0.
Ensuite, voyons pourquoi le résultat de PHP8%-3 est 0.
Tout d’abord, nous devons comprendre les règles de traitement PHP pour les opérations modulaires. Dans des circonstances normales, le résultat de l’arithmétique modulo devrait être un entier non négatif. Mais en PHP, le signe du reste est le même que celui du dividende. Autrement dit, si le dividende est positif, le reste est également positif ; si le dividende est négatif, le reste est également négatif.
Dans cet exemple, 8 est le dividende et -3 est le diviseur. Puisque 8 est un nombre positif, le reste devrait également être positif. Mais selon les règles PHP, le signe du reste est le même que celui du dividende, donc le reste est négatif. C’est pourquoi le résultat de 8%-3 est -1 au lieu du 1 normal.
Alors la question est : pourquoi le résultat de 8%-3 n'est-il pas -1, mais 0 ?
En fait, c'est parce qu'il existe une exception à l'arithmétique modulaire en PHP. Lorsque la valeur absolue du dividende est inférieure à la valeur absolue du diviseur, le résultat de l'opération modulo est égal au dividende. Autrement dit, le résultat de 8%-3 est égal à 8. C'est pourquoi le résultat de 8%-3 est 0.
Cette situation peut également être vérifiée par des calculs mathématiques. Nous savons que -3 divise 8 une fois, avec un reste de 2. Selon les règles PHP, le signe du reste est le même que celui du dividende, donc le reste est -2. Mais les règles spéciales de PHP changent le reste à 0, donc le résultat devient 8%3=0.
Bien que cette règle spéciale ne soit pas mathématiquement stricte, elle nous aide à résoudre certains cas particuliers en PHP. Dans la programmation réelle, nous pouvons rencontrer certains problèmes qui nécessitent de prendre en compte cette situation particulière. En comprenant cette règle, nous pouvons mieux gérer ces problèmes et éviter les erreurs.
Pour résumer, la raison pour laquelle PHP8%-3 est 0 est parce que PHP a une règle spéciale lorsqu'il s'agit d'opérations modulaires lorsque la valeur absolue du dividende est inférieure à la valeur absolue du diviseur, le résultat de l'opération modulaire. est égal au dividende. Cette règle spéciale nous aide à résoudre certains cas particuliers, mais n’est pas mathématiquement rigoureuse. Comprendre cette règle peut nous aider à mieux gérer ces situations particulières et à éviter les erreurs.
Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!

Outils d'IA chauds

Undresser.AI Undress
Application basée sur l'IA pour créer des photos de nu réalistes

AI Clothes Remover
Outil d'IA en ligne pour supprimer les vêtements des photos.

Undress AI Tool
Images de déshabillage gratuites

Clothoff.io
Dissolvant de vêtements AI

AI Hentai Generator
Générez AI Hentai gratuitement.

Article chaud

Outils chauds

Bloc-notes++7.3.1
Éditeur de code facile à utiliser et gratuit

SublimeText3 version chinoise
Version chinoise, très simple à utiliser

Envoyer Studio 13.0.1
Puissant environnement de développement intégré PHP

Dreamweaver CS6
Outils de développement Web visuel

SublimeText3 version Mac
Logiciel d'édition de code au niveau de Dieu (SublimeText3)
 Guide d'installation et de mise à niveau de PHP 8.4 pour Ubuntu et Debian
Dec 24, 2024 pm 04:42 PM
Guide d'installation et de mise à niveau de PHP 8.4 pour Ubuntu et Debian
Dec 24, 2024 pm 04:42 PM
PHP 8.4 apporte plusieurs nouvelles fonctionnalités, améliorations de sécurité et de performances avec une bonne quantité de dépréciations et de suppressions de fonctionnalités. Ce guide explique comment installer PHP 8.4 ou mettre à niveau vers PHP 8.4 sur Ubuntu, Debian ou leurs dérivés. Bien qu'il soit possible de compiler PHP à partir des sources, son installation à partir d'un référentiel APT comme expliqué ci-dessous est souvent plus rapide et plus sécurisée car ces référentiels fourniront les dernières corrections de bogues et mises à jour de sécurité à l'avenir.
 Date et heure de CakePHP
Sep 10, 2024 pm 05:27 PM
Date et heure de CakePHP
Sep 10, 2024 pm 05:27 PM
Pour travailler avec la date et l'heure dans cakephp4, nous allons utiliser la classe FrozenTime disponible.
 Discuter de CakePHP
Sep 10, 2024 pm 05:28 PM
Discuter de CakePHP
Sep 10, 2024 pm 05:28 PM
CakePHP est un framework open source pour PHP. Il vise à faciliter grandement le développement, le déploiement et la maintenance d'applications. CakePHP est basé sur une architecture de type MVC à la fois puissante et facile à appréhender. Modèles, vues et contrôleurs gu
 Téléchargement de fichiers CakePHP
Sep 10, 2024 pm 05:27 PM
Téléchargement de fichiers CakePHP
Sep 10, 2024 pm 05:27 PM
Pour travailler sur le téléchargement de fichiers, nous allons utiliser l'assistant de formulaire. Voici un exemple de téléchargement de fichiers.
 CakePHP créant des validateurs
Sep 10, 2024 pm 05:26 PM
CakePHP créant des validateurs
Sep 10, 2024 pm 05:26 PM
Le validateur peut être créé en ajoutant les deux lignes suivantes dans le contrôleur.
 Journalisation CakePHP
Sep 10, 2024 pm 05:26 PM
Journalisation CakePHP
Sep 10, 2024 pm 05:26 PM
Se connecter à CakePHP est une tâche très simple. Il vous suffit d'utiliser une seule fonction. Vous pouvez enregistrer les erreurs, les exceptions, les activités des utilisateurs, les actions entreprises par les utilisateurs, pour tout processus en arrière-plan comme cronjob. La journalisation des données dans CakePHP est facile. La fonction log() est fournie
 Comment configurer Visual Studio Code (VS Code) pour le développement PHP
Dec 20, 2024 am 11:31 AM
Comment configurer Visual Studio Code (VS Code) pour le développement PHP
Dec 20, 2024 am 11:31 AM
Visual Studio Code, également connu sous le nom de VS Code, est un éditeur de code source gratuit – ou environnement de développement intégré (IDE) – disponible pour tous les principaux systèmes d'exploitation. Avec une large collection d'extensions pour de nombreux langages de programmation, VS Code peut être c
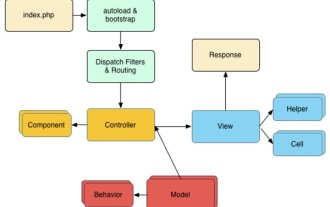 Guide rapide CakePHP
Sep 10, 2024 pm 05:27 PM
Guide rapide CakePHP
Sep 10, 2024 pm 05:27 PM
CakePHP est un framework MVC open source. Cela facilite grandement le développement, le déploiement et la maintenance des applications. CakePHP dispose d'un certain nombre de bibliothèques pour réduire la surcharge des tâches les plus courantes.






