
Les processus gaussiens du modèle de noyau (KMGP) sont des outils sophistiqués permettant de gérer la complexité de divers ensembles de données. Il étend le concept des processus gaussiens traditionnels à travers les fonctions du noyau. Cet article discutera en détail de la base théorique, des applications pratiques et des défis des KMGP.
Le processus gaussien du modèle de noyau est une extension du processus gaussien traditionnel et est utilisé dans l'apprentissage automatique et les statistiques. Avant de comprendre kmgp, vous devez maîtriser les connaissances de base du processus gaussien, puis comprendre le rôle du modèle de noyau.
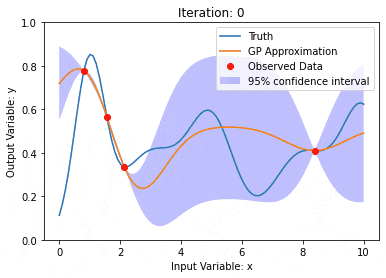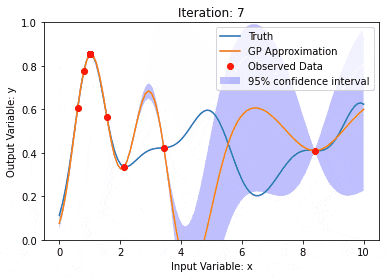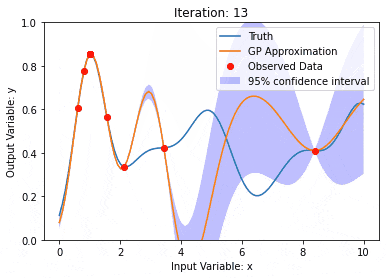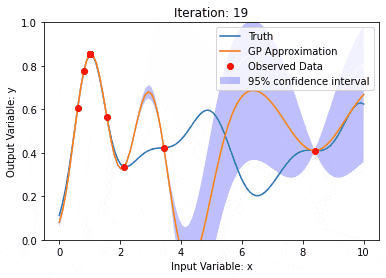
Les processus gaussiens sont des ensembles de variables aléatoires, avec un nombre limité de variables distribuées conjointement par gaussiennes, utilisées pour définir des distributions de probabilité de fonctions.
Le processus gaussien est couramment utilisé dans les tâches de régression et de classification de l'apprentissage automatique et peut être utilisé pour ajuster la distribution de probabilité des données.
Une caractéristique importante des processus gaussiens est la capacité de fournir des estimations et des prédictions d'incertitude, ce qui est très utile pour comprendre que la confiance d'une prédiction est aussi importante que la prédiction elle-même.
Dans un processus gaussien, la fonction noyau (ou fonction de covariance) est utilisée pour mesurer la similarité entre différents points de données. La fonction noyau prend deux entrées et calcule le score de similarité entre elles.
Il existe différents types de noyaux tels que les fonctions de base linéaires, polynomiales et radiales (RBF). Chaque noyau a des caractéristiques différentes et le noyau approprié peut être sélectionné en fonction du problème.
Dans les processus gaussiens, la modélisation du noyau est le processus de sélection et d'optimisation des fonctions du noyau pour capturer au mieux les modèles sous-jacents dans les données. Cette étape est très importante car la sélection et la configuration du noyau peuvent affecter de manière significative les performances du processus gaussien.
KMGPs est une extension du standard GP (Gaussian Process), axé sur l'application des fonctions du noyau. Par rapport aux GP standard, les KMGP accordent plus d'attention à la personnalisation de fonctions de noyau complexes ou conçues sur mesure en fonction de types spécifiques de données ou de problèmes. Cette approche est particulièrement utile lorsque les données sont complexes et que les fonctions standard du noyau ne parviennent pas à capturer les relations sous-jacentes. Cependant, la conception et le réglage des fonctions du noyau dans les KMGP sont difficiles et nécessitent souvent une connaissance approfondie du domaine et une expérience professionnelle dans le domaine problématique et la modélisation statistique.
Le processus gaussien du modèle de noyau est un outil sophistiqué d'apprentissage statistique, offrant un moyen flexible et puissant de modéliser des ensembles de données complexes. Ils sont particulièrement appréciés pour leur capacité à fournir des estimations d’incertitude et leur adaptabilité à rapprocher différents types de données grâce à des rapprochements personnalisés.
Les noyaux bien conçus de KMGP peuvent modéliser des phénomènes complexes tels que les tendances non linéaires, la périodicité et l'hétéroscédasticité (niveaux de bruit variables) dans les données. Cela nécessite donc une connaissance approfondie du domaine et une compréhension approfondie de la modélisation statistique.
KMGP a des applications dans de nombreux domaines. En géostatistique, ils modélisent les données spatiales pour capturer la variation géographique sous-jacente. En finance, ils sont utilisés pour prédire les cours des actions, expliquant la nature instable et complexe des marchés financiers. En robotique et en systèmes de contrôle, les KMGP modélisent et prédisent le comportement des systèmes dynamiques sous incertitude.
Nous utilisons un ensemble de données synthétiques pour créer un exemple de code Python complet. Nous utilisons ici une bibliothèque GPy, qui est une bibliothèque en python spécialisée dans la gestion des processus gaussiens.
pip install numpy matplotlib GPy
Importer une bibliothèque
import numpy as np import matplotlib.pyplot as plt import GPy
Ensuite, nous créerons un ensemble de données synthétiques en utilisant numpy.
X = np.linspace(0, 10, 100)[:, None] Y = np.sin(X) + np.random.normal(0, 0.1, X.shape)
Définir et entraîner un modèle de processus gaussien à l'aide de GPy
kernel = GPy.kern.RBF(input_dim=1, variance=1., lengthscale=1.) model = GPy.models.GPRegression(X, Y, kernel) model.optimize(messages=True)
Après avoir entraîné le modèle, nous l'utiliserons pour faire des prédictions sur l'ensemble de données de test. Tracez ensuite un graphique pour visualiser les performances du modèle.
X_test = np.linspace(-2, 12, 200)[:, None] Y_pred, Y_var = model.predict(X_test) plt.figure(figsize=(10, 5)) plt.plot(X_test, Y_pred, 'r-', lw=2, label='Prediction') plt.fill_between(X_test.flatten(), (Y_pred - 2*np.sqrt(Y_var)).flatten(), (Y_pred + 2*np.sqrt(Y_var)).flatten(), alpha=0.5, color='pink', label='Confidence Interval') plt.scatter(X, Y, c='b', label='Training Data') plt.xlabel('X') plt.ylabel('Y') plt.title('Kernel Modeled Gaussian Process Regression') plt.legend() plt.show()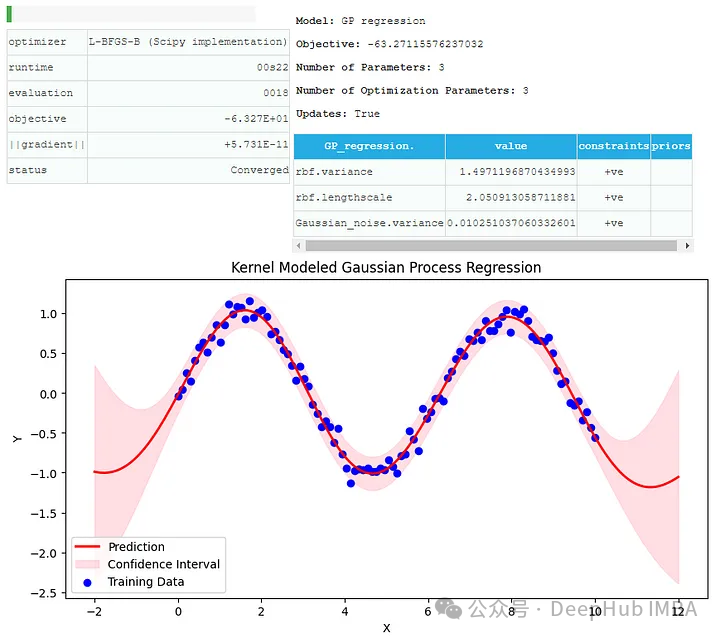
Ici, nous appliquons le modèle de régression du processus gaussien avec le noyau RBF, et nous pouvons voir les données de prédiction et d'entraînement et l'intervalle de confiance.
Le processus gaussien du modèle de noyau représente une avancée majeure dans le domaine de l'apprentissage statistique, fournissant un cadre flexible et puissant pour comprendre des ensembles de données complexes. GPy contient également essentiellement toutes les fonctions du noyau que nous pouvons voir. Ce qui suit est une capture d'écran du document officiel :
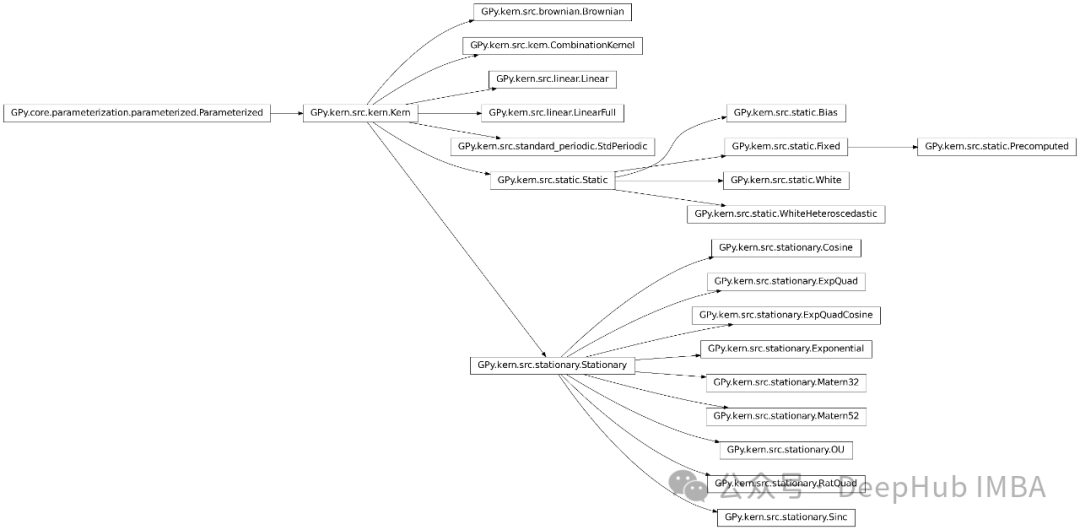
Pour différentes données, vous devez choisir différents hyperparamètres du noyau de fonction du noyau. Voici le flux officiel de GPy A. le tableau est donné
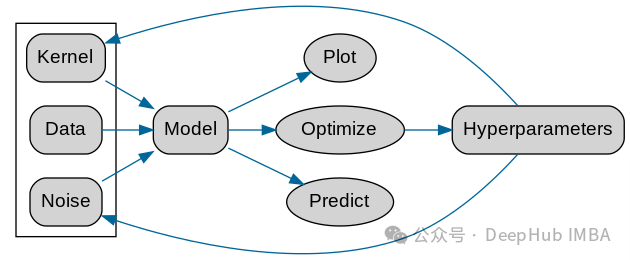
Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!
 Quelle plateforme est la meilleure pour le trading de devises virtuelles ?
Quelle plateforme est la meilleure pour le trading de devises virtuelles ?
 Introduction aux méthodes de maintenance des variateurs de fréquence
Introduction aux méthodes de maintenance des variateurs de fréquence
 Comment établir un réseau local sous XP
Comment établir un réseau local sous XP
 Quels sont les paramètres du chapiteau ?
Quels sont les paramètres du chapiteau ?
 Comment entrer en mode de récupération sur un ordinateur Windows 10
Comment entrer en mode de récupération sur un ordinateur Windows 10
 Quels sont les composants de base d'un ordinateur ?
Quels sont les composants de base d'un ordinateur ?
 Le rôle de l'attribut caption
Le rôle de l'attribut caption
 Tutoriel d'utilisation du serveur cloud
Tutoriel d'utilisation du serveur cloud