 Périphériques technologiques
Périphériques technologiques
 IA
IA
 Les grands modèles peuvent également être découpés, et Microsoft SliceGPT augmente considérablement l'efficacité de calcul de LAMA-2.
Les grands modèles peuvent également être découpés, et Microsoft SliceGPT augmente considérablement l'efficacité de calcul de LAMA-2.
Les grands modèles peuvent également être découpés, et Microsoft SliceGPT augmente considérablement l'efficacité de calcul de LAMA-2.
Les modèles linguistiques à grande échelle (LLM) comportent généralement des milliards de paramètres et sont formés sur des milliards de jetons. Cependant, ces modèles sont très coûteux à former et à déployer. Afin de réduire les besoins de calcul, diverses techniques de compression de modèles sont souvent utilisées.
Ces techniques de compression de modèles peuvent généralement être divisées en quatre catégories : la distillation, la décomposition tensorielle (y compris la factorisation de bas rang), l'élagage et la quantification. Les méthodes d'élagage existent depuis un certain temps, mais beaucoup nécessitent un réglage fin de la récupération (RFT) après l'élagage pour maintenir les performances, ce qui rend l'ensemble du processus coûteux et difficile à faire évoluer.
Des chercheurs de l'ETH Zurich et de Microsoft ont proposé une solution à ce problème, appelée SliceGPT. L'idée principale de cette méthode est de réduire la dimension d'intégration du réseau en supprimant des lignes et des colonnes dans la matrice de pondération pour maintenir les performances du modèle. L’émergence de SliceGPT apporte une solution efficace à ce problème.
Les chercheurs ont noté qu'avec SliceGPT, ils étaient capables de compresser de grands modèles en quelques heures à l'aide d'un seul GPU, maintenant ainsi des performances compétitives dans les tâches de génération et en aval, même sans RFT. Actuellement, la recherche a été acceptée par l’ICLR 2024.

- Titre de l'article : SLICEGPT : COMPRESSER DE GRANDS MODÈLES DE LANGAGE EN SUPPRIMANT DES LIGNES ET DES COLONNES
- Lien de l'article : https://arxiv.org/pdf/2401 .1 5024.pdf
La méthode d'élagage fonctionne en mettant à zéro certains éléments de la matrice de poids dans le LLM et en mettant à jour sélectivement les éléments environnants pour compenser. Il en résulte un modèle clairsemé qui ignore certaines opérations en virgule flottante lors du passage direct du réseau neuronal, améliorant ainsi l'efficacité du calcul.
Le degré de parcimonie et le mode de parcimonie sont des facteurs qui déterminent l'amélioration relative de la vitesse de calcul. Lorsque le mode clairsemé est plus raisonnable, il apportera davantage d’avantages informatiques. Contrairement à d'autres méthodes d'élagage, SliceGPT élague en coupant (en coupant !) des lignes ou des colonnes entières de la matrice de poids. Avant la résection, le réseau subit une transformation qui maintient les prédictions inchangées mais permet des processus de cisaillement légèrement affectés.
Le résultat est que la matrice de poids est réduite, la transmission du signal est affaiblie et la dimension du réseau neuronal est réduite.
La figure 1 ci-dessous compare la méthode SliceGPT avec les méthodes de parcimonie existantes.
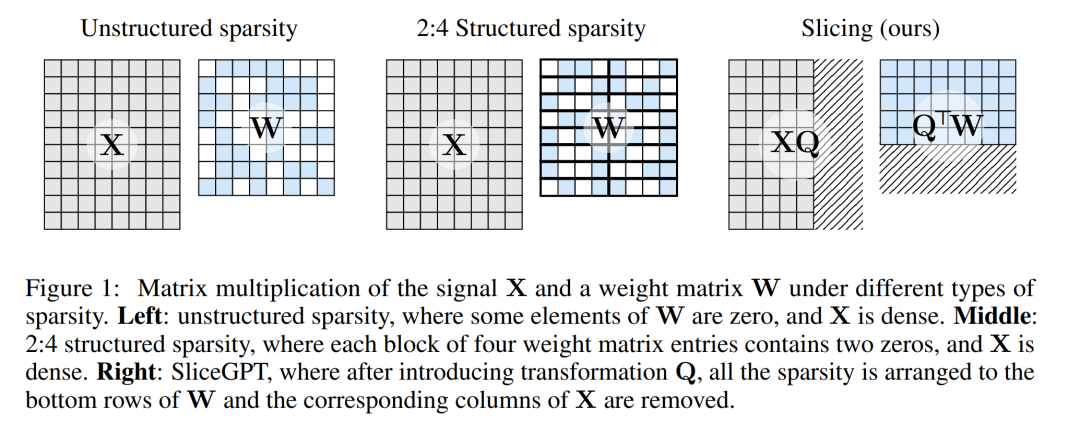
Grâce à des expériences approfondies, les auteurs ont découvert que SliceGPT peut supprimer jusqu'à 25 % des paramètres du modèle (y compris les intégrations) pour les modèles LLAMA-2 70B, OPT 66B et Phi-2, tout en conservant 99 % de modèles denses respectivement, 99 % et 90 % de performance des tâches sans échantillon.
Les modèles traités par SliceGPT peuvent fonctionner sur moins de GPU et s'exécuter plus rapidement sans aucune optimisation de code supplémentaire : sur un GPU grand public de 24 Go, l'auteur a comparé le calcul d'inférence total de LLAMA-2 à 70 B. Le montant a été réduit à 64 % sur le modèle dense ; sur le GPU A100 de 40 Go, ils l'ont réduit à 66 %.
De plus, ils ont également proposé un nouveau concept, l'invariance informatique dans les réseaux Transformer, qui rend SliceGPT possible.
SliceGPT en détail
La méthode SliceGPT s'appuie sur l'invariance informatique inhérente à l'architecture Transformer. Cela signifie que vous pouvez appliquer une transformation orthogonale à la sortie d'un composant, puis l'annuler dans le composant suivant. Les auteurs ont observé que les opérations RMSNorm effectuées entre les blocs du réseau n'affectent pas la transformation : ces opérations sont commutatives.
Dans l'article, l'auteur présente d'abord comment obtenir l'invariance dans un réseau Transformer avec des connexions RMSNorm, puis explique comment convertir un réseau formé avec des connexions LayerNorm en RMSNorm. Ensuite, ils introduisent la méthode d'utilisation de l'analyse en composantes principales (ACP) pour calculer la transformation de chaque couche, projetant ainsi le signal entre les blocs sur ses composantes principales. Enfin, ils montrent comment la suppression de composants principaux mineurs correspond à une coupure de lignes ou de colonnes du réseau.
Invariance computationnelle du réseau de transformateurs
Utilisez Q pour représenter la matrice orthogonale : 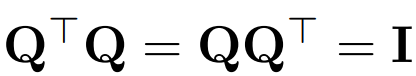
- Notez que multiplier un vecteur
Supposons que X_ℓ soit la sortie d'un bloc de transformateur. Après avoir été traité par RMSNorm, il est entré dans le bloc suivant sous la forme de RMSNorm (X_ℓ). Si vous insérez une couche linéaire avec une matrice orthogonale Q avant RMSNorm et Q^⊤ après RMSNorm, le réseau restera inchangé car chaque ligne de la matrice de signal est multipliée par Q, normalisée et multipliée par Q^ ⊤. Nous avons ici :
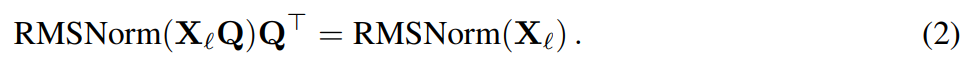
Maintenant, puisque chaque attention ou bloc FFN du réseau effectue une opération linéaire sur l'entrée et la sortie, l'opération supplémentaire Q peut être absorbée dans la couche linéaire du module. Étant donné que le réseau contient des connexions résiduelles, Q doit également être appliqué aux sorties de toutes les couches précédentes (jusqu'à l'intégration) et de toutes les couches suivantes (jusqu'à la tête LM).
Une fonction invariante fait référence à une fonction dont la transformation d'entrée n'entraîne pas de modification de la sortie. Dans l'exemple de cet article, n'importe quelle transformation orthogonale Q peut être appliquée aux poids du transformateur sans changer le résultat, de sorte que le calcul peut être effectué dans n'importe quel état de transformation. Les auteurs appellent cela invariance computationnelle et la définissent dans le théorème suivant.
Théorème 1 : Soient 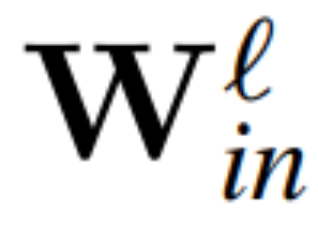 et
et 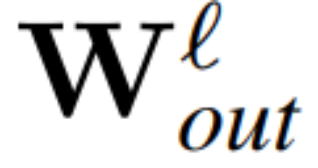 la matrice de poids de la couche linéaire du ℓème bloc du réseau de transformateurs connecté par RMSNorm,
la matrice de poids de la couche linéaire du ℓème bloc du réseau de transformateurs connecté par RMSNorm, 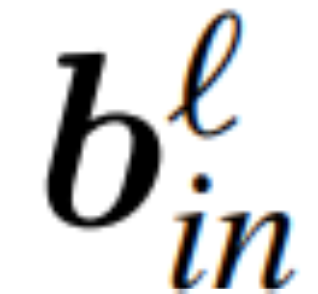 et
et 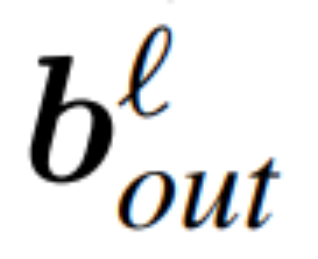 les biais correspondants (le cas échéant), W_embd et W_head sont les matrice d'intégration et matrice de tête. En supposant que Q est une matrice orthogonale de dimension D, alors le réseau suivant est équivalent au réseau de transformateur d'origine :
les biais correspondants (le cas échéant), W_embd et W_head sont les matrice d'intégration et matrice de tête. En supposant que Q est une matrice orthogonale de dimension D, alors le réseau suivant est équivalent au réseau de transformateur d'origine :
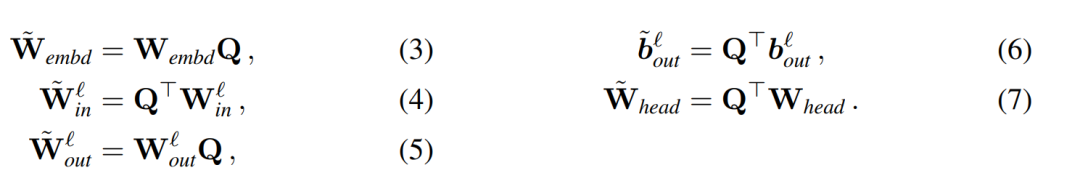
La copie du biais d'entrée et du biais de tête :
peut être effectuée via l'algorithme 1 pour prouver que le réseau converti calcule les mêmes résultats que le réseau d'origine.
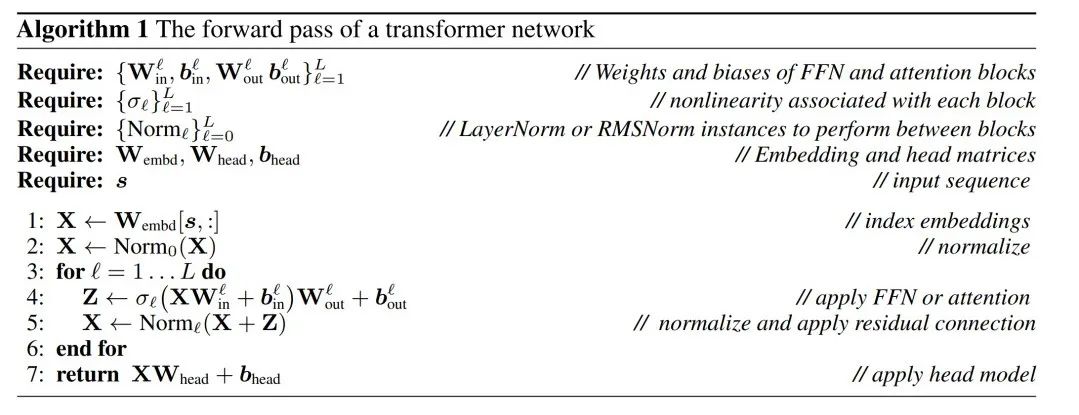
LayerNorm Transformer peut être converti en RMSNorm
Transformer L'invariance informatique du réseau s'applique uniquement aux réseaux connectés RMSNorm. Avant de traiter un réseau à l'aide de LayerNorm, les auteurs convertissent d'abord le réseau en RMSNorm en absorbant les blocs linéaires de LayerNorm dans des blocs adjacents.
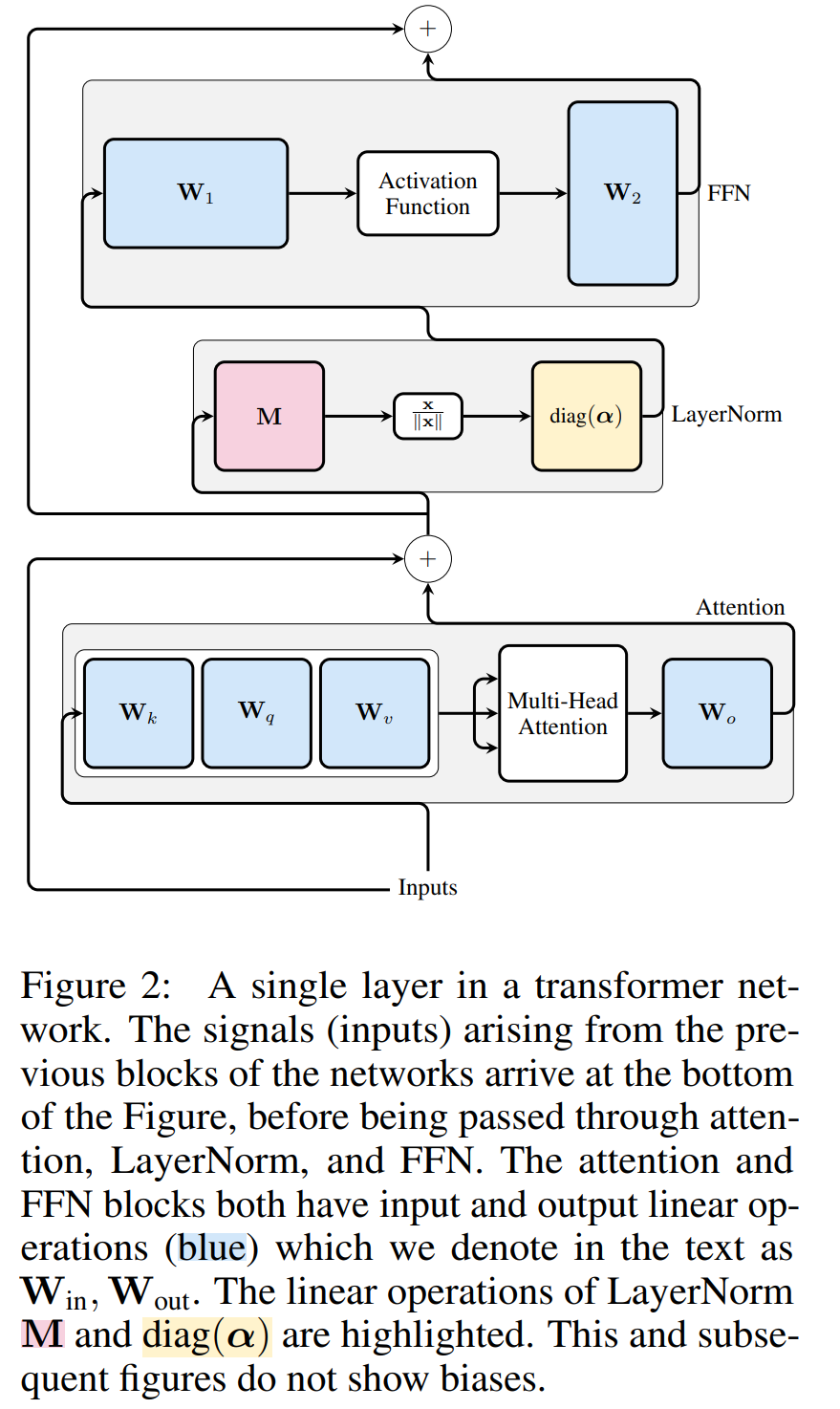
La figure 3 montre cette transformation du réseau Transformateur (voir Figure 2). Dans chaque bloc, les auteurs multiplient la matrice de sortie W_out par la matrice de soustraction moyenne M, qui prend en compte la soustraction moyenne dans LayerNorm suivante. La matrice d'entrée W_in est prémultipliée par la proportion du bloc LayerNorm précédent. La matrice d'intégration W_embd doit subir une soustraction moyenne et W_head doit être redimensionnée en fonction de la proportion du dernier LayerNorm. Il s'agit d'un simple changement dans l'ordre des opérations et n'affectera pas la sortie du réseau.
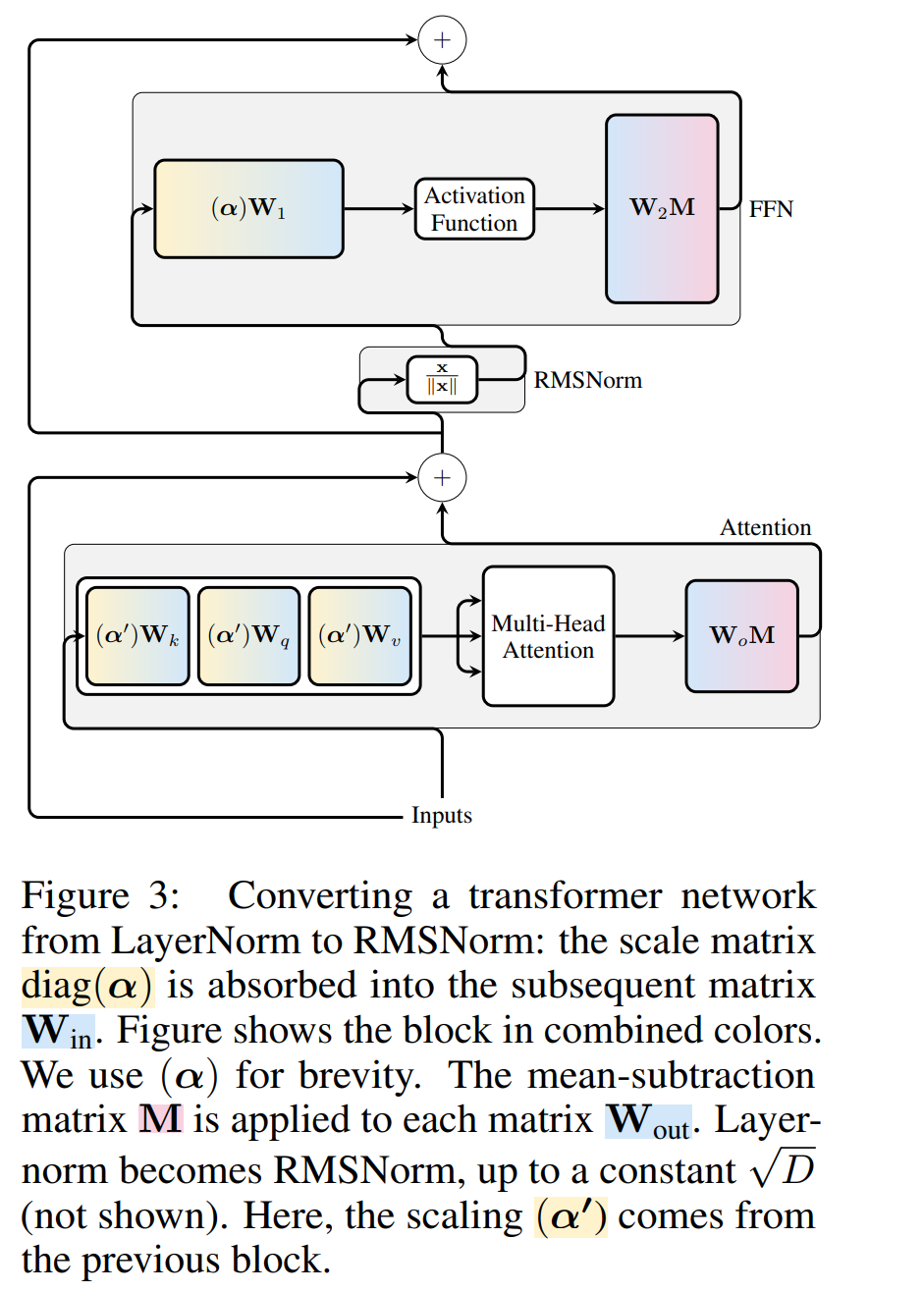
Transformation de chaque bloc
Maintenant que chaque LayerNorm du transformateur a été convertie en RMSNorm, n'importe quel Q peut être sélectionné pour modifier le modèle. Le plan initial de l'auteur était de collecter les signaux du modèle, d'utiliser ces signaux pour construire une matrice orthogonale, puis de supprimer des parties du réseau. Ils ont rapidement découvert que les signaux des différents blocs du réseau n’étaient pas alignés et qu’ils devaient donc appliquer une matrice orthogonale différente, ou Q_ℓ, à chaque bloc.
Si la matrice orthogonale utilisée dans chaque bloc est différente, le modèle ne changera pas. La méthode de preuve est la même que le théorème 1, à l'exception de la ligne 5 de l'algorithme 1. Ici vous pouvez voir que la sortie de la connexion résiduelle et le bloc doivent avoir la même rotation. Afin de résoudre ce problème, l'auteur modifie la connexion résiduelle en transformant linéairement le résidu. 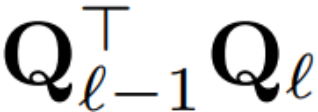
La figure 4 montre comment effectuer différentes rotations sur différents blocs en effectuant des opérations linéaires supplémentaires sur la connexion résiduelle. Contrairement aux modifications apportées à la matrice de poids, ces opérations supplémentaires ne peuvent pas être précalculées et ajoutent une petite surcharge (D × D) au modèle. Néanmoins, ces opérations sont nécessaires pour découper le modèle, et vous pouvez constater que la vitesse globale augmente.
Pour calculer la matrice Q_ℓ, l'auteur a utilisé PCA. Ils sélectionnent un ensemble de données d'étalonnage dans l'ensemble d'apprentissage, l'exécutent dans le modèle (après avoir converti l'opération LayerNorm en RMSNorm) et extraient la matrice orthogonale de cette couche. Plus précisément, si ils utilisent la sortie du réseau transformé pour calculer la matrice orthogonale de la couche suivante. Plus précisément, si 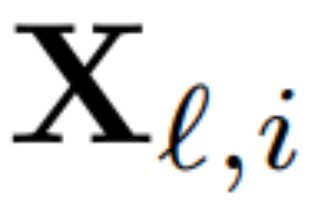 est la sortie du ℓ-ème module RMSNorm pour la i-ème séquence dans l'ensemble de données d'étalonnage, calculez :
est la sortie du ℓ-ème module RMSNorm pour la i-ème séquence dans l'ensemble de données d'étalonnage, calculez : 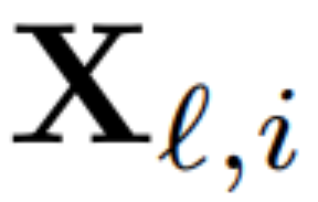

et définissez Q_ℓ comme étant le vecteur propre de C_ℓ, dans ordre décroissant des valeurs propres Trier.成 Suppression 分 L'objectif de l'analyse en composantes principales est d'obtenir la matrice de données X et de calculer la représentation de faible dimension Z et la reconstruction approximative :
Parmi eux, Q est
est Le vecteur propre, D, est une petite matrice de suppression D × D (contenant D petites colonnes d'une matrice homotope D × D) utilisée pour supprimer certaines colonnes sur le côté gauche de la matrice. La reconstruction est L_2 optimale dans le sens où QD est une application linéaire qui minimise . 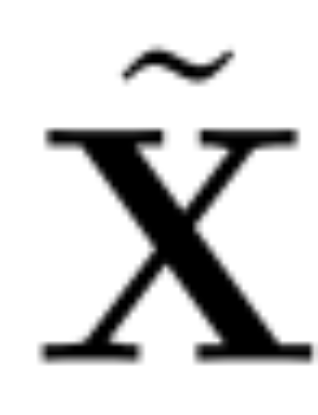
insérée dans la connexion résiduelle (voir Figure 4). 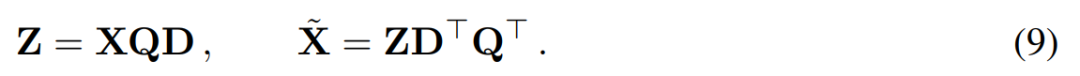
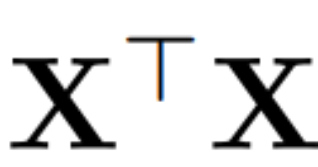
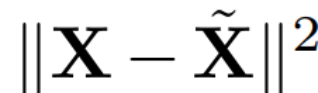 Tâche de génération
Tâche de génération
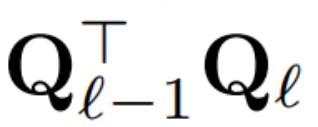
L'auteur a mené une évaluation des performances sur les séries de modèles OPT et LAMA-2 de différentes tailles après avoir été découpées par SliceGPT et SparseGPT dans le WikiText-2 base de données. Le tableau 1 montre la complexité retenue après différents niveaux d'élagage du modèle. Comparé au modèle LAMA-2, SliceGPT a montré des performances supérieures lorsqu'il est appliqué au modèle OPT, ce qui est cohérent avec les spéculations de l'auteur basées sur l'analyse du spectre du modèle.
Les performances de SliceGPT s'amélioreront à mesure que la taille du modèle augmente. Le mode SparseGPT 2:4 fonctionne moins bien que SliceGPT avec un écrêtage de 25 % pour tous les modèles de la série LLAMA-2. Pour l’OPT, on constate que la parcimonie du modèle avec un taux de résection de 30 % est meilleure que celle de 2 : 4 dans tous les modèles sauf le modèle 2,7B.
Tâche à échantillon zéro
L'auteur a utilisé cinq tâches : PIQA, WinoGrande, HellaSwag, ARC-e et ARCc pour évaluer les performances de SliceGPT sur la tâche à échantillon zéro. Ils ont utilisé le harnais d'évaluation LM par défaut. dans le paramètre d’évaluation.
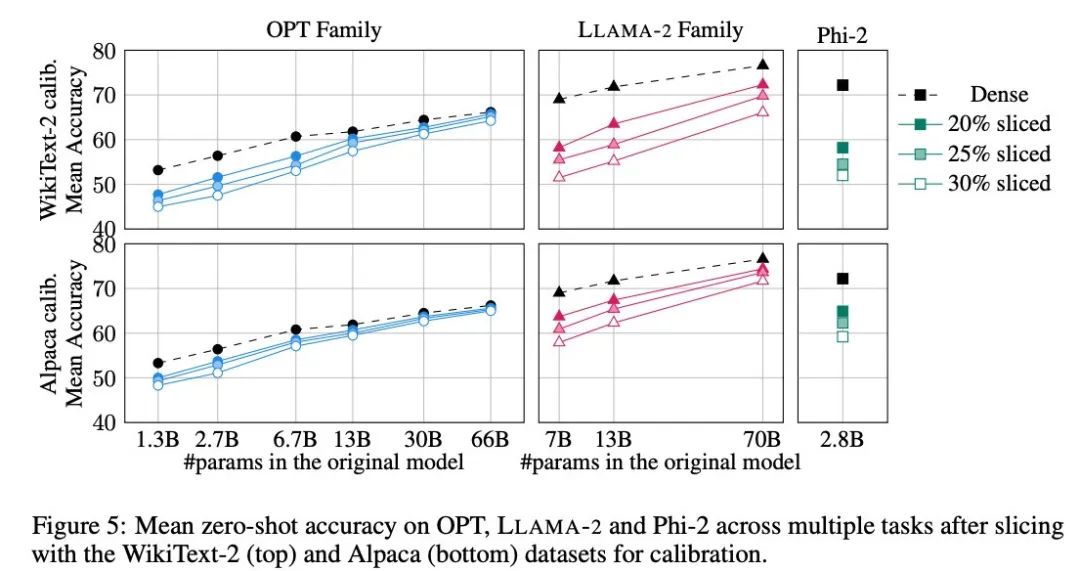
La figure 5 montre les scores moyens obtenus par le modèle personnalisé sur les tâches ci-dessus. La ligne supérieure de la figure montre la précision moyenne de SliceGPT dans WikiText-2, et la ligne inférieure montre la précision moyenne de SliceGPT dans Alpaca. Des conclusions similaires peuvent être observées à partir des résultats comme dans la tâche de génération : le modèle OPT est plus adaptable à la compression que le modèle LAMA-2, et plus le modèle est grand, moins la diminution de précision après l'élagage est évidente.
L'auteur a testé l'effet de SliceGPT sur un petit modèle comme Phi-2. Le modèle Phi-2 garni a des performances comparables au modèle LAMA-2 7B garni. Les plus grands modèles OPT et LAMA-2 peuvent être compressés efficacement, et SliceGPT ne perd que quelques points de pourcentage en supprimant 30 % du modèle OPT 66B.
L'auteur a également mené une expérience de réglage fin de la récupération (RFT). Un petit nombre de RFT ont été réalisés sur les modèles rognés LLAMA-2 et Phi-2 à l'aide de LoRA.
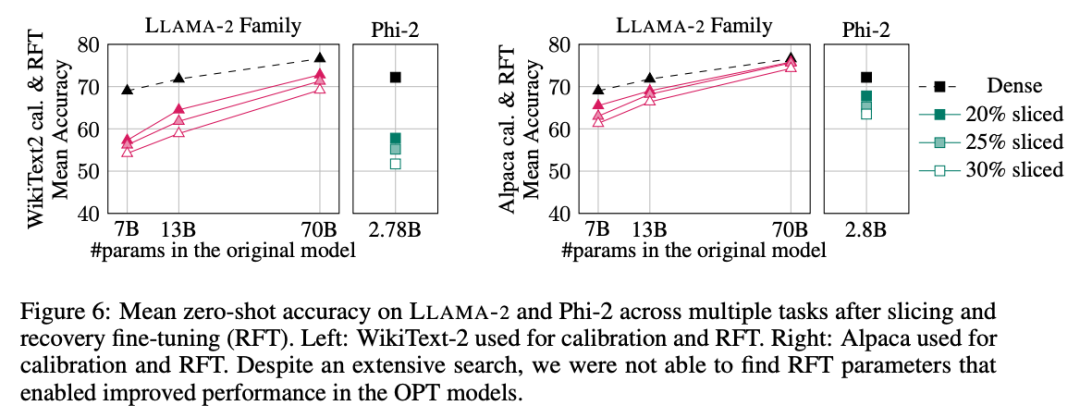
Les résultats expérimentaux sont présentés dans la figure 6. On peut constater qu'il existe des différences significatives dans les résultats de RFT entre les ensembles de données WikiText-2 et Alpaca, et le modèle montre de meilleures performances dans l'ensemble de données Alpaca. Les auteurs pensent que la raison de la différence est que les tâches de l'ensemble de données Alpaca sont plus proches des tâches de référence.
Pour le plus grand modèle LLAMA-2 70B, après avoir élagué 30 % et effectué RFT, la précision moyenne finale dans l'ensemble de données Alpaca est de 74,3 % et la précision du modèle dense d'origine est de 76,6 %. Le modèle sur mesure LLAMA-2 70B conserve environ 51,6B de paramètres et son débit est considérablement amélioré.
L'auteur a également constaté que Phi-2 était incapable de restaurer la précision d'origine du modèle élagué dans l'ensemble de données WikiText-2, mais il pouvait restaurer quelques points de pourcentage de précision dans l'ensemble de données Alpaca. Phi-2, coupé de 25 % et RFT, a une précision moyenne de 65,2 % dans l'ensemble de données Alpaca, et la précision du modèle dense d'origine est de 72,2 %. Le modèle tronqué conserve les paramètres 2,2B et conserve 90,3 % de la précision du modèle 2,8B. Cela montre que même les petits modèles de langage peuvent être élagués efficacement.
Benchmark Throughput
Différent des méthodes d'élagage traditionnelles, SliceGPT introduit une parcimonie (structurée) dans la matrice X : toute la colonne X est coupée, réduisant ainsi la dimension d'intégration. Cette approche améliore à la fois la complexité de calcul (nombre d'opérations en virgule flottante) du modèle de compression SliceGPT et améliore l'efficacité du transfert de données.
Sur un GPU H100 de 80 Go, définissez la longueur de la séquence sur 128 et doublez par lots la longueur de la séquence pour trouver le débit maximum jusqu'à ce que la mémoire du GPU soit épuisée ou que le débit diminue. Les auteurs ont comparé le débit des modèles élagués à 25 % et 50 % au modèle dense d'origine sur un GPU H100 de 80 Go. Les modèles réduits de 25 % ont obtenu une amélioration du débit jusqu'à 1,55 fois.
Avec un écrêtage de 50 %, le plus grand modèle atteint des augmentations substantielles de débit de 3,13x et 1,87x en utilisant un seul GPU. Cela montre que lorsque le nombre de GPU est fixé, le débit du modèle élagué atteindra respectivement 6,26 fois et 3,75 fois celui du modèle dense d'origine.
Après un élagage de 50 %, bien que la complexité retenue par SliceGPT dans WikiText2 soit pire que SparseGPT 2:4, le débit dépasse de loin la méthode SparseGPT. Pour les modèles de taille 13B, le débit peut également s'améliorer pour les modèles plus petits sur des GPU grand public avec moins de mémoire.
Temps d'inférence
L'auteur a également étudié le temps d'exécution de bout en bout du modèle compressé à l'aide de SliceGPT. Le tableau 2 compare le temps requis pour générer un seul jeton pour les modèles OPT 66B et LAMA-2 70B sur les GPU Quadro RTX6000 et A100. On constate que sur le GPU RTX6000, après avoir réduit le modèle de 25 %, la vitesse d'inférence est augmentée de 16 à 17 % ; sur le GPU A100, la vitesse est augmentée de 11 à 13 % ; Pour LLAMA-2 70B, l'effort de calcul requis avec le GPU RTX6000 est réduit de 64 % par rapport au modèle dense d'origine. L'auteur attribue cette amélioration au remplacement par SliceGPT de la matrice de poids d'origine par une matrice de poids plus petite et à l'utilisation de grains denses, ce qui ne peut pas être obtenu par d'autres schémas d'élagage.
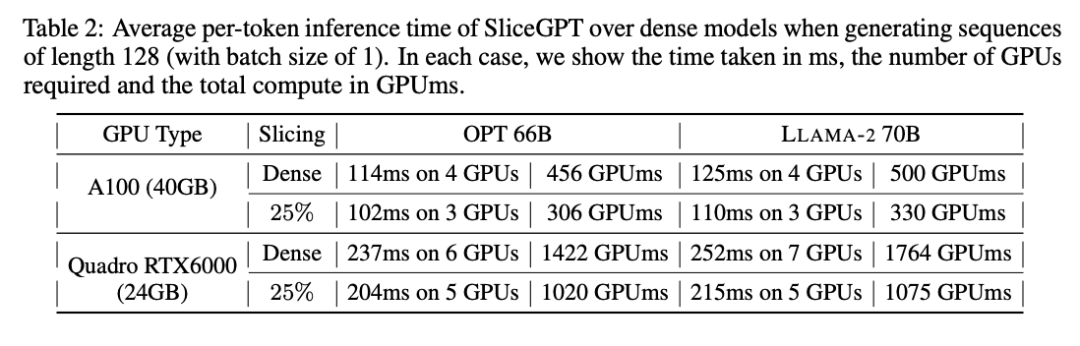
Les auteurs ont déclaré qu'au moment de la rédaction, leur base de référence SparseGPT 2:4 n'était pas en mesure d'améliorer les performances de bout en bout. Au lieu de cela, ils ont comparé SliceGPT à SparseGPT 2:4 en comparant le temps relatif de chaque opération dans la couche de transformateur. Ils ont constaté que pour les grands modèles, SliceGPT (25 %) était compétitif avec SparseGPT (2:4) en termes d'amélioration de la vitesse et de perplexité.
Coût de calcul
Tous les modèles LLLAMA-2, OPT et Phi-2 peuvent être segmentés en 1 à 3 heures sur un seul GPU. Comme le montre le tableau 3, avec un réglage fin de la récupération, tous les LM peuvent être compressés en 1 à 5 heures.

Pour plus d'informations, veuillez vous référer au document original.
Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!

Outils d'IA chauds

Undresser.AI Undress
Application basée sur l'IA pour créer des photos de nu réalistes

AI Clothes Remover
Outil d'IA en ligne pour supprimer les vêtements des photos.

Undress AI Tool
Images de déshabillage gratuites

Clothoff.io
Dissolvant de vêtements AI

Video Face Swap
Échangez les visages dans n'importe quelle vidéo sans effort grâce à notre outil d'échange de visage AI entièrement gratuit !

Article chaud

Outils chauds

Bloc-notes++7.3.1
Éditeur de code facile à utiliser et gratuit

SublimeText3 version chinoise
Version chinoise, très simple à utiliser

Envoyer Studio 13.0.1
Puissant environnement de développement intégré PHP

Dreamweaver CS6
Outils de développement Web visuel

SublimeText3 version Mac
Logiciel d'édition de code au niveau de Dieu (SublimeText3)

Sujets chauds
 Prévisions des prix WorldCoin (WLD) 2025-2031: WLD atteindra-t-il 4 $ d'ici 2031?
Apr 21, 2025 pm 02:42 PM
Prévisions des prix WorldCoin (WLD) 2025-2031: WLD atteindra-t-il 4 $ d'ici 2031?
Apr 21, 2025 pm 02:42 PM
WorldCoin (WLD) se démarque sur le marché des crypto-monnaies avec ses mécanismes uniques de vérification biométrique et de protection de la vie privée, attirant l'attention de nombreux investisseurs. WLD a permis de se produire avec remarquablement parmi les Altcoins avec ses technologies innovantes, en particulier en combinaison avec la technologie d'Intelligence artificielle OpenAI. Mais comment les actifs numériques se comporteront-ils au cours des prochaines années? Prédons ensemble le prix futur de WLD. Les prévisions de prix de 2025 WLD devraient atteindre une croissance significative de la WLD en 2025. L'analyse du marché montre que le prix moyen du WLD peut atteindre 1,31 $, avec un maximum de 1,36 $. Cependant, sur un marché baissier, le prix peut tomber à environ 0,55 $. Cette attente de croissance est principalement due à WorldCoin2.
 Aavenomics est une recommandation pour modifier le jeton Aave Protocol et introduire le rachat de jetons, qui a atteint le nombre de personnes quorum.
Apr 21, 2025 pm 06:24 PM
Aavenomics est une recommandation pour modifier le jeton Aave Protocol et introduire le rachat de jetons, qui a atteint le nombre de personnes quorum.
Apr 21, 2025 pm 06:24 PM
Aavenomics est une proposition de modification du jeton de protocole Aave et d'introduire des dépens de jetons, qui a mis en œuvre un quorum pour Aavedao. Marc Zeller, fondateur de l'Aave Project Chain (ACI), l'a annoncé sur X, notant qu'il marque une nouvelle ère pour l'accord. Marc Zeller, fondateur de l'Aave Chain Initiative (ACI), a annoncé sur X que la proposition d'Aavenomics comprend la modification du jeton Aave Protocol et l'introduction de dépens de jetons, a obtenu un quorum pour Aavedao. Selon Zeller, cela marque une nouvelle ère pour l'accord. Les membres d'Aavedao ont voté massivement pour soutenir la proposition, qui était de 100 par semaine mercredi
 Pourquoi la hausse ou la baisse des prix de monnaie virtuelle? Pourquoi la hausse ou la baisse des prix de monnaie virtuelle?
Apr 21, 2025 am 08:57 AM
Pourquoi la hausse ou la baisse des prix de monnaie virtuelle? Pourquoi la hausse ou la baisse des prix de monnaie virtuelle?
Apr 21, 2025 am 08:57 AM
Les facteurs de la hausse des prix des devises virtuels comprennent: 1. Une augmentation de la demande du marché, 2. Daisser l'offre, 3. Stimulé de nouvelles positives, 4. Sentiment du marché optimiste, 5. Environnement macroéconomique; Les facteurs de déclin comprennent: 1. Daissement de la demande du marché, 2. AUGMENT DE L'OFFICATION, 3. Strike of Negative News, 4. Pespimiste Market Sentiment, 5. Environnement macroéconomique.
 Que signifie la transaction transversale? Quelles sont les transactions transversales?
Apr 21, 2025 pm 11:39 PM
Que signifie la transaction transversale? Quelles sont les transactions transversales?
Apr 21, 2025 pm 11:39 PM
Échanges qui prennent en charge les transactions transversales: 1. Binance, 2. UniSwap, 3. Sushiswap, 4. Curve Finance, 5. Thorchain, 6. 1inch Exchange, 7. DLN Trade, ces plateformes prennent en charge les transactions d'actifs multi-chaînes via diverses technologies.
 Comment gagner des récompenses de plateaux aériens du noyau sur la stratégie de processus complète de la binance
Apr 21, 2025 pm 01:03 PM
Comment gagner des récompenses de plateaux aériens du noyau sur la stratégie de processus complète de la binance
Apr 21, 2025 pm 01:03 PM
Dans le monde animé des crypto-monnaies, de nouvelles opportunités émergent toujours. À l'heure actuelle, l'activité aérienne de Kerneldao (noyau) attire beaucoup l'attention et attire l'attention de nombreux investisseurs. Alors, quelle est l'origine de ce projet? Quels avantages le support BNB peut-il en tirer? Ne vous inquiétez pas, ce qui suit le révélera un par un pour vous.
 'Black Monday Sell' est une journée difficile pour l'industrie de la crypto-monnaie
Apr 21, 2025 pm 02:48 PM
'Black Monday Sell' est une journée difficile pour l'industrie de la crypto-monnaie
Apr 21, 2025 pm 02:48 PM
Le plongeon sur le marché des crypto-monnaies a provoqué la panique parmi les investisseurs, et Dogecoin (Doge) est devenu l'une des zones les plus difficiles. Son prix a fortement chuté et le verrouillage de la valeur totale de la finance décentralisée (DEFI) (TVL) a également connu une baisse significative. La vague de vente de "Black Monday" a balayé le marché des crypto-monnaies, et Dogecoin a été le premier à être touché. Son Defitvl a chuté aux niveaux de 2023 et le prix de la devise a chuté de 23,78% au cours du dernier mois. Le Defitvl de Dogecoin est tombé à un minimum de 2,72 millions de dollars, principalement en raison d'une baisse de 26,37% de l'indice de valeur SOSO. D'autres plates-formes de Defi majeures, telles que le Dao et Thorchain ennuyeux, TVL ont également chuté de 24,04% et 20, respectivement.
 Les dix premières recommandations de plate-forme gratuites pour les données en temps réel sur les marchés du cercle de devises sont publiées
Apr 22, 2025 am 08:12 AM
Les dix premières recommandations de plate-forme gratuites pour les données en temps réel sur les marchés du cercle de devises sont publiées
Apr 22, 2025 am 08:12 AM
Les plateformes de données de crypto-monnaie adaptées aux débutants incluent CoinmarketCap et la trompette non à petites choses. 1. CoinmarketCap fournit des classements mondiaux de prix, de valeur marchande et de volume de trading pour les besoins novices et d'analyse de base. 2. La citation non à petites choses fournit une interface adaptée aux Chinois, adaptée aux utilisateurs chinois afin de projeter rapidement des projets potentiels à faible risque.
 Classement des échanges à effet de levier dans le cercle des devises Les dernières recommandations des dix premiers échanges à effet de levier dans le cercle des devises
Apr 21, 2025 pm 11:24 PM
Classement des échanges à effet de levier dans le cercle des devises Les dernières recommandations des dix premiers échanges à effet de levier dans le cercle des devises
Apr 21, 2025 pm 11:24 PM
Les plates-formes qui ont des performances exceptionnelles dans le commerce, la sécurité et l'expérience utilisateur en effet de levier en 2025 sont: 1. OKX, adaptés aux traders à haute fréquence, fournissant jusqu'à 100 fois l'effet de levier; 2. Binance, adaptée aux commerçants multi-monnaies du monde entier, offrant un effet de levier 125 fois élevé; 3. Gate.io, adapté aux joueurs de dérivés professionnels, fournissant 100 fois l'effet de levier; 4. Bitget, adapté aux novices et aux commerçants sociaux, fournissant jusqu'à 100 fois l'effet de levier; 5. Kraken, adapté aux investisseurs stables, fournissant 5 fois l'effet de levier; 6. BUTBIT, adapté aux explorateurs Altcoin, fournissant 20 fois l'effet de levier; 7. Kucoin, adapté aux commerçants à faible coût, fournissant 10 fois l'effet de levier; 8. Bitfinex, adapté au jeu senior





