Abandonnez l'architecture codeur-décodeur et utilisez le modèle de diffusion pour la détection des contours avec de meilleurs résultats. L'Université nationale de technologie de la défense a proposé DiffusionEdge.

Les réseaux actuels de détection des contours profonds adoptent généralement une architecture d'encodeur-décodeur, qui contient des modules d'échantillonnage ascendant et descendant pour mieux extraire les fonctionnalités à plusieurs niveaux. Cependant, cette structure limite le réseau à produire des résultats de détection de contour précis et détaillés.

En réponse à ce problème, un article présenté à l'AAAI 2024 propose une nouvelle solution.

• Titre de l'article : DiffusionEdge : Diffusion Probabilistic Model for Crisp Edge Detection
• Auteurs : Ye Yunfan (Université nationale de technologie de la défense), Xu Kai (Université nationale de technologie de la défense), Huang Yuxing (Université nationale de technologie de défense), Yi Renjiao (Université nationale de technologie de défense), Cai Zhiping (Université nationale de technologie de défense)
• Lien papier : https://arxiv.org/abs/2401.02032
• Code open source : https://github.com/ GuHuangAI/DiffusionEdge

Le laboratoire iGRAPE de l'Université nationale de technologie de la défense a proposé une nouvelle méthode pour les tâches de détection de bords 2D. Cette méthode utilise un modèle de probabilité de diffusion pour générer des cartes de résultats de bord au cours d'un processus de débruitage itératif d'apprentissage. Afin de réduire la consommation de ressources informatiques, cette méthode utilise l'espace latent pour entraîner le réseau et introduit un module de distillation d'incertitude pour optimiser les performances. Dans le même temps, cette méthode adopte également une architecture découplée pour accélérer le processus de débruitage et introduit un filtre de Fourier adaptatif pour ajuster les caractéristiques. Grâce à ces conceptions, la méthode est capable de s'entraîner de manière stable avec des ressources limitées et de prédire des cartes de contour claires et précises avec moins de stratégies d'augmentation. Les résultats expérimentaux montrent que cette méthode surpasse considérablement les autres méthodes en termes d’exactitude et de précision sur quatre ensembles de données de référence publics.

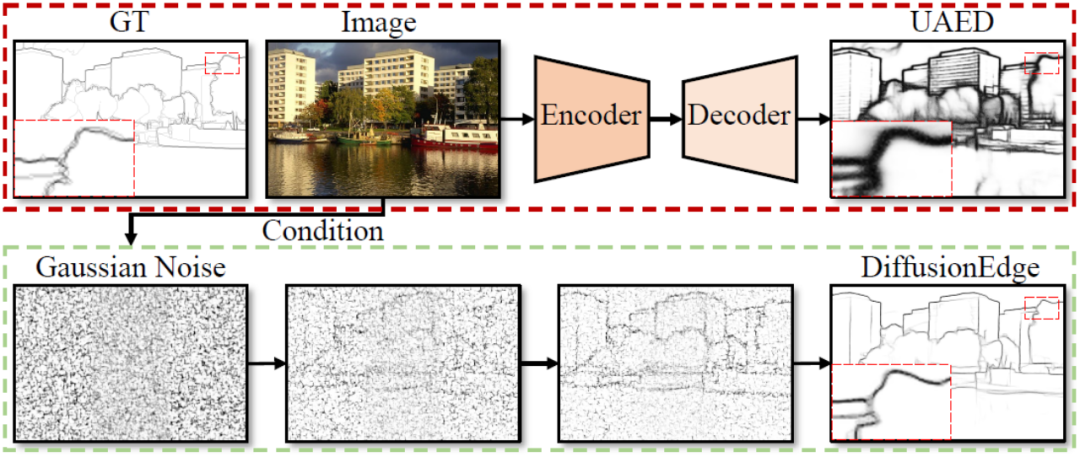
Figure 1 Exemple de processus de détection de contour et avantages basés sur un modèle de probabilité de diffusion

Les points d'innovation de cet article incluent :

Proposition d'un modèle de diffusion DiffusionEdge pour les tâches de détection de contour, qui ne nécessitent un post-traitement. Cela vous permet de prédire des cartes de contours plus fines et plus précises.

Afin de résoudre les difficultés d'application du modèle de diffusion, nous avons conçu une variété de techniques pour garantir que la méthode apprend de manière stable dans l'espace latent. Dans le même temps, nous conservons également les connaissances préalables sur l’incertitude au niveau des pixels et filtrons de manière adaptative les caractéristiques latentes dans l’espace de Fourier.

3. Des expériences comparatives approfondies menées sur quatre ensembles de données de référence publiques de détection de bords démontrent que DiffusionEdge présente d'excellents avantages en termes de performances en termes de précision et de finesse.

Travail associé

Les méthodes basées sur l'apprentissage en profondeur utilisent généralement une structure de codage et de décodage comprenant un échantillonnage ascendant et descendant pour intégrer des fonctionnalités multicouches [1-2], ou intègrent des informations d'incertitude provenant de plusieurs annotations pour améliorer la détection des contours. .précision[3]. Cependant, naturellement limitée par une telle structure, la carte de résultats de bord générée est trop épaisse pour les tâches en aval et repose fortement sur le post-traitement. Le problème doit encore être résolu. Bien que de nombreux travaux aient été explorés dans les fonctions de perte [4-5] et les stratégies de correction d'étiquettes [6] pour permettre au réseau de produire des bords plus fins, cet article estime que ce domaine a encore besoin d'une méthode pouvant être utilisée sans aucun module Edge supplémentaire. des détecteurs qui répondent directement à la précision et à la finesse sans aucune étape de post-traitement.

Le modèle de diffusion est un type de modèle génératif basé sur la chaîne de Markov, qui restaure progressivement des échantillons de données cibles grâce au processus d'apprentissage de débruitage. Les modèles de diffusion ont montré d'excellentes performances dans des domaines tels que la vision par ordinateur, le traitement du langage naturel et la génération audio. Non seulement cela, en utilisant des images ou d'autres entrées modales comme conditions supplémentaires, cela montre également un grand potentiel dans les tâches de perception, telles que la segmentation d'images [7], la détection de cibles [8] et l'estimation d'attitude [9], etc.

Description de la méthode

Le cadre global de la méthode DiffusionEdge proposée dans cet article est présenté dans la figure 2. Inspirée de travaux antérieurs, cette méthode entraîne un modèle de diffusion avec une structure découplée dans l'espace latent et entre des images comme indices conditionnels supplémentaires. Cette méthode introduit un filtre de Fourier adaptatif pour l'analyse de fréquence et, afin de conserver les informations d'incertitude au niveau des pixels provenant de plusieurs annotateurs et de réduire les besoins en ressources informatiques, elle utilise également directement l'optimisation des pertes d'entropie croisée de manière distillée.

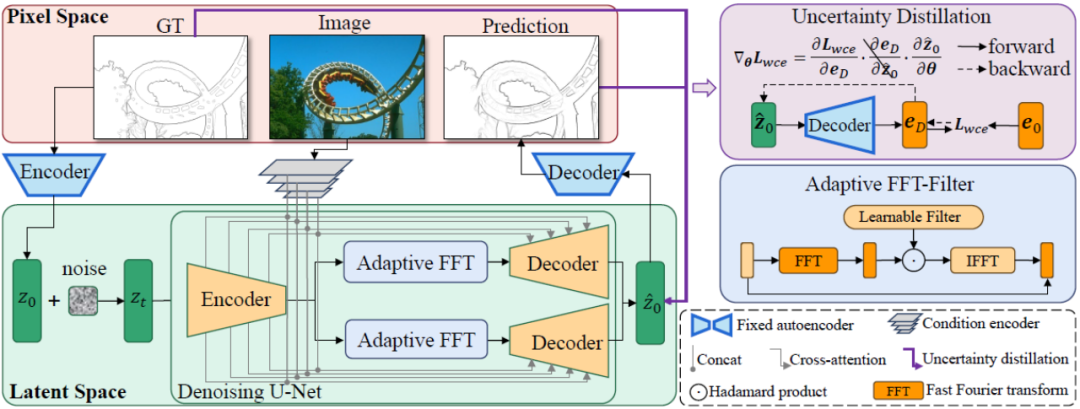
Figure 2 Diagramme schématique de la structure globale de DiffusionEdge

Comme le modèle de diffusion actuel est en proie à des problèmes tels qu'un trop grand nombre d'étapes d'échantillonnage et un temps d'inférence trop long, cette méthode s'inspire du DDM [10] et utilise également des diffusion. Architecture du modèle pour accélérer le processus d’inférence d’échantillonnage. Parmi eux, le processus de diffusion directe découplé est contrôlé par une combinaison de probabilité de transition explicite et de processus Wiener standard :

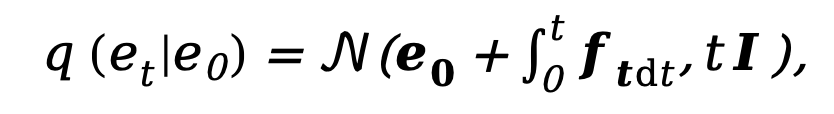
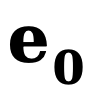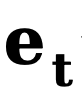où et représentent respectivement le bord initial et le bord de bruit, 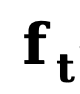fait référence au bord inverse. fonction de transfert pour les dégradés. Semblable à DDM, cette méthode utilise la fonction constante 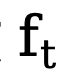par défaut, et son processus inverse correspondant peut être exprimé comme suit :

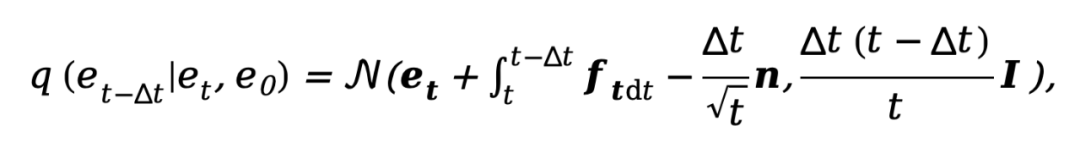
où 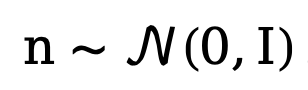. Afin d'entraîner le modèle de diffusion découplé, la méthode nécessite une supervision simultanée des composantes de données et de bruit, par conséquent, l'objectif d'entraînement peut être paramétré comme :

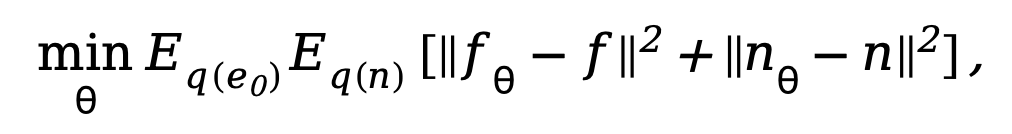
où 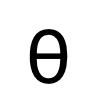est le paramètre dans le réseau de débruitage. Étant donné que le modèle de diffusion nécessitera trop de coûts de calcul s'il est formé dans l'espace image d'origine, se référant à l'idée de [11], la méthode proposée dans cet article transfère le processus de formation dans un espace latent avec 4 fois le taille de l’espace de sous-échantillonnage.

Comme le montre la figure 2, cette méthode entraîne d'abord une paire de réseaux d'encodeur et de décodeur automatiques. L'encodeur compresse l'annotation de bord en une variable latente, et le décodeur est utilisé pour récupérer de cette variable latente. . De cette façon, pendant la phase de formation du réseau de débruitage basé sur la structure U-Net, cette méthode fixe le poids de la paire de réseaux d'auto-encodeur et de décodeur et entraîne le processus de débruitage dans l'espace latent, ce qui peut réduire considérablement le temps de calcul. coût du réseau. consommation de ressources tout en conservant de bonnes performances.

Afin d'améliorer les performances finales du réseau, la méthode proposée dans cet article introduit un module capable de filtrer de manière adaptative différentes caractéristiques de fréquence lors de l'opération de découplage. Comme le montre le coin inférieur gauche de la figure 2, cette méthode intègre le filtre à transformée de Fourier rapide adaptatif (filtre FFT adaptatif) dans le réseau Unet de débruitage avant l'opération de découplage pour filtrer et séparer de manière adaptative dans le domaine fréquentiel la carte des bords extérieurs et le bruit. Composants. Plus précisément, étant donné la fonctionnalité d'encodeur 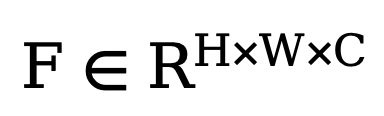, la méthode effectue d'abord une transformation de Fourier bidimensionnelle (FFT) le long de la dimension spatiale et représente la caractéristique transformée sous la forme 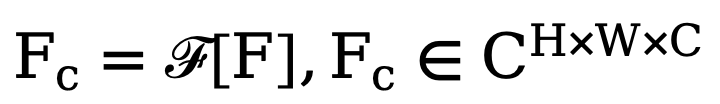. Ensuite, afin d'entraîner ce module de filtrage spectral adaptatif, une carte de poids apprenable 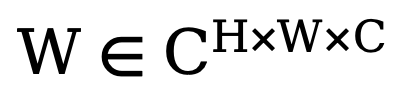est construite et son W est multiplié par Fc. Les filtres spectraux peuvent ajuster globalement des fréquences spécifiques, et les poids appris peuvent être adaptés à différents cas de fréquence de distributions cibles dans différents ensembles de données. En filtrant de manière adaptative les composants indésirables, cette méthode mappe les caractéristiques du domaine fréquentiel vers le domaine spatial via une opération de transformation de Fourier rapide inverse (IFFT). Enfin, en introduisant en plus la connexion résiduelle de , nous évitons de filtrer complètement toutes les informations utiles. Le processus ci-dessus peut être décrit par la formule suivante :

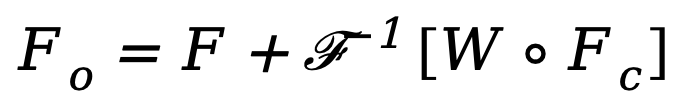
où 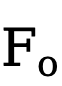est la caractéristique de sortie et o représente le produit Hadamard.

En raison du déséquilibre élevé entre le nombre de pixels de bord et de non-bord (la plupart des pixels sont des arrière-plans sans bord), en référence à des travaux antérieurs, nous introduisons également une fonction de perte tenant compte de l'incertitude pour l'entraînement. Plus précisément, comme la véritable probabilité de bord du i-ème pixel, pour le i-ème pixel dans la j-ème carte de bord, sa valeur est 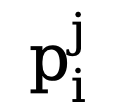, alors la perte WCE tenant compte de l'incertitude est calculée comme suit :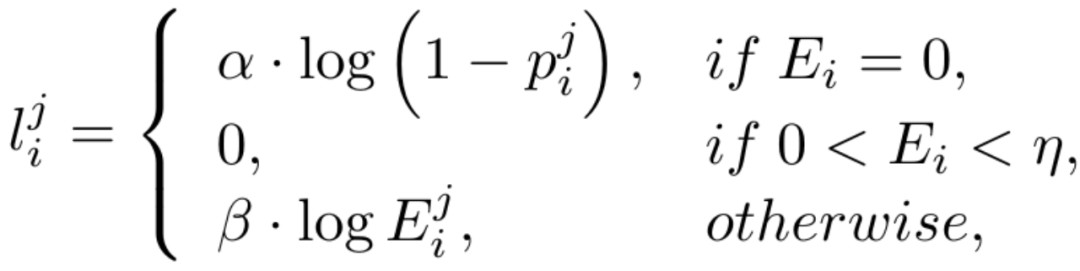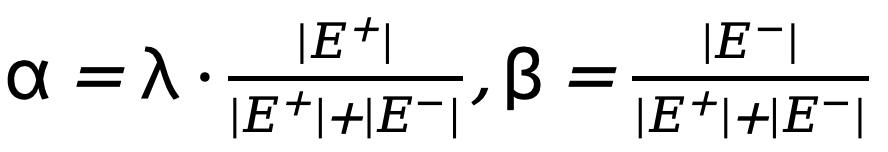

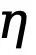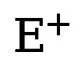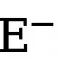où , où est le seuil qui détermine les pixels de bord incertains dans l'annotation de valeur vraie. Si la valeur du pixel est supérieure à 0 et inférieure à ce seuil, de tels échantillons de pixels flous avec une confiance insuffisante seront utilisés dans l'optimisation ultérieure. processus est ignoré (la fonction de perte est 0). et représentent respectivement le nombre de pixels de bord et non-bord dans la carte de bord annotée de vérité terrain. est le poids utilisé pour équilibrer 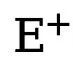et 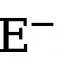(fixé à 1,1). Par conséquent, la fonction de perte finale pour chaque carte de bord est calculée comme suit : .

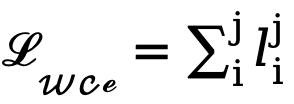Ignorer les pixels flous à faible confiance pendant le processus d'optimisation peut éviter la confusion du réseau, rendre le processus de formation plus stable et améliorer les performances du modèle. Cependant, il est presque impossible d’appliquer directement la perte d’entropie croisée binaire dans un espace latent qui est désaligné à la fois numériquement et spatialement. En particulier, la perte d'entropie croisée sensible à l'incertitude utilise un seuil 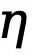(généralement de 0 à 1) pour déterminer si un pixel est un bord, défini à partir de l'espace image, tandis que les variables latentes suivent une distribution normale et ont complètement portée et signification pratique différentes. De plus, l’incertitude au niveau des pixels est difficile à concilier avec différentes tailles de caractéristiques latentes codées et sous-échantillonnées, et les deux ne sont pas directement compatibles. Par conséquent, l’application directe de la perte d’entropie croisée pour optimiser les variables latentes conduit inévitablement à une perception incorrecte de l’incertitude.

D'un autre côté, on peut choisir de décoder les variables latentes au niveau de l'image, supervisant ainsi directement la carte des résultats de bord prédits en utilisant une perte d'entropie croisée sensible à l'incertitude. Malheureusement, cette implémentation permet aux gradients de paramètres rétropropagés de passer à travers le réseau d'auto-encodeurs redondants, ce qui rend difficile le transfert efficace des gradients. De plus, des calculs de gradient supplémentaires dans le réseau d'auto-encodeurs entraîneront d'énormes coûts de consommation de mémoire GPU, ce qui viole l'intention initiale de cette méthode de concevoir un détecteur de bord pratique et est difficile à généraliser aux applications pratiques. Par conséquent, cette méthode propose une perte de distillation d'incertitude, qui peut directement optimiser le gradient sur l'espace latent. Plus précisément, soit la variable latente reconstruite , le décodeur du réseau d'auto-encodeurs soit D et le résultat du bord décodé soit eD. envisage de calculer directement le gradient de la perte d'entropie croisée binaire consciente de l'incertitude 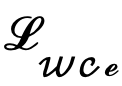sur la base de la règle de chaîne. La méthode de calcul spécifique est la suivante :

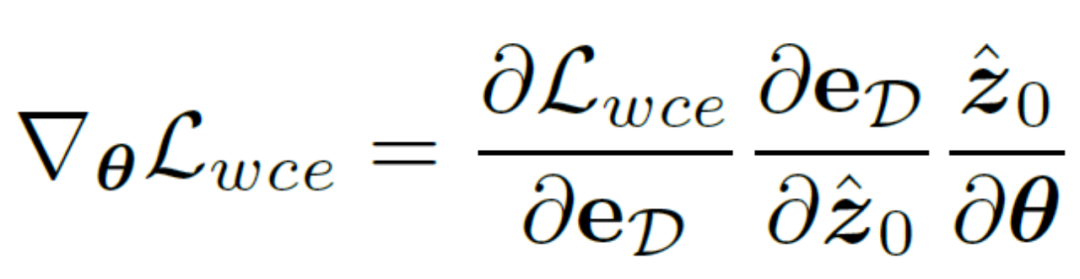
Afin d'éliminer l'impact négatif du réseau d'auto-encodeurs, cette méthode Le. l'autoencodeur 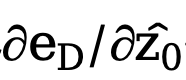est directement sauté pour passer le dégradé et la méthode de calcul du dégradé 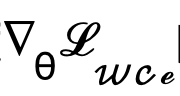est modifiée et ajustée à :

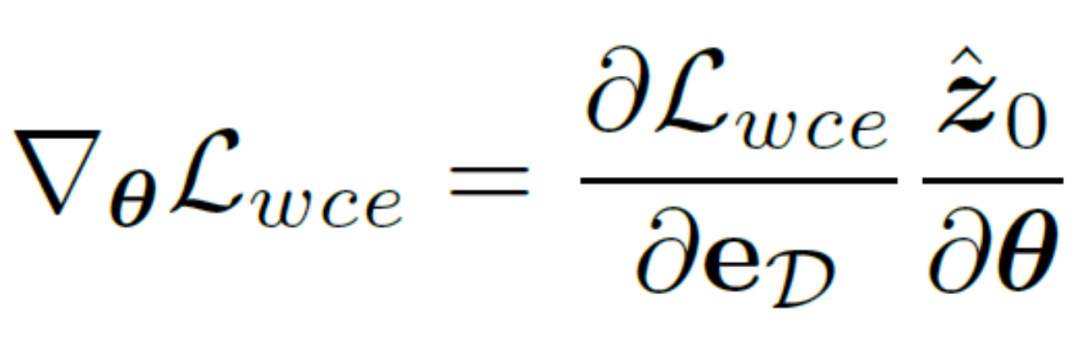
Une telle implémentation réduit considérablement le coût de calcul et permet une optimisation directe sur les variables latentes à l'aide de fonctions de perte sensibles à l'incertitude. De cette manière, combiné à une perte de poids variable dans le temps 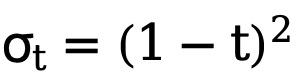qui change de manière adaptative avec le nombre d'étapes t, l'objectif final d'optimisation de l'entraînement de cette méthode peut être exprimé comme suit :

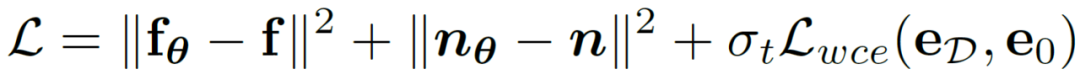
Résultats expérimentaux

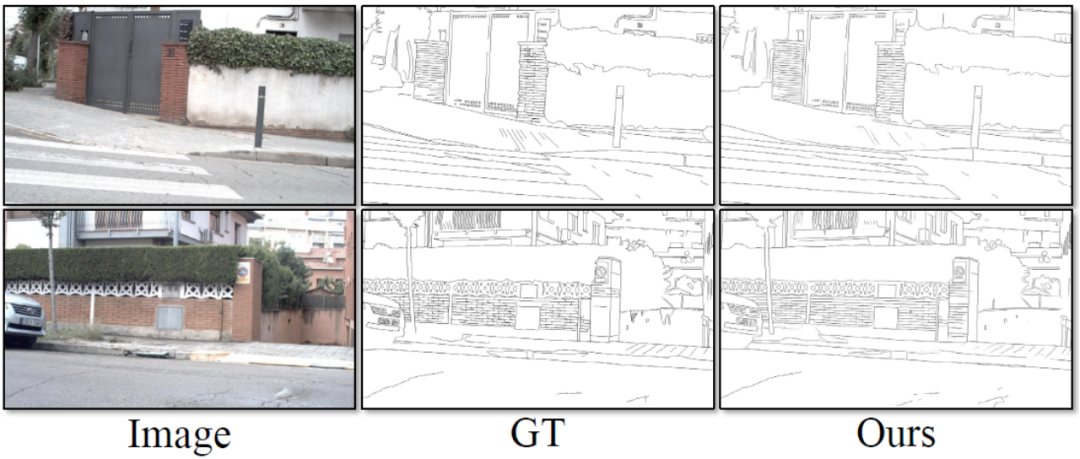
Ce La méthode comporte quatre expériences ont été menées sur des ensembles de données standards publics pour la détection des contours qui sont largement utilisés dans le domaine : BSDS, NYUDv2, Multicue et BIPED. Puisqu’il est difficile d’étiqueter les données de détection de contour et que la quantité de données étiquetées est relativement faible, les méthodes précédentes utilisent généralement diverses stratégies pour améliorer l’ensemble de données. Par exemple, les images dans BSDS sont améliorées par le retournement horizontal (2×), la mise à l'échelle (3×) et la rotation (16×), ce qui donne un ensemble d'entraînement 96 fois plus grand que la version originale. Les stratégies d'amélioration courantes utilisées par les méthodes précédentes sur d'autres ensembles de données sont résumées dans le tableau 1, où F représente le retournement horizontal, S représente la mise à l'échelle, R représente la rotation, C représente le recadrage et G représente la correction gamma. La différence est que cette méthode n'a besoin que d'utiliser des patchs d'image recadrés de manière aléatoire de 320320 pour entraîner toutes les données. Dans l'ensemble de données BSDS, cette méthode utilise uniquement un retournement et une mise à l'échelle aléatoires, et ses résultats de comparaison quantitative sont présentés dans le tableau 2. Dans les ensembles de données NYUDv2, Multicue et BIPED, la méthode doit uniquement être entraînée avec des retournements aléatoires. Avec moins de stratégies d’amélioration, cette méthode fonctionne mieux que les méthodes précédentes sur divers ensembles de données et divers indicateurs. En observant les résultats de prédiction de la figure 3-5, nous pouvons voir que DiffusionEdge peut apprendre et prédire des résultats de détection de contours qui sont presque les mêmes que la distribution gt. L'avantage de résultats de prédiction précis et clairs est très important pour les tâches en aval qui nécessitent un affinement. , et a également démontré son grand potentiel pour être directement appliqué aux tâches ultérieures.

Tableau 1 Stratégies d'amélioration utilisées par les méthodes précédentes sur quatre ensembles de données de détection de contours

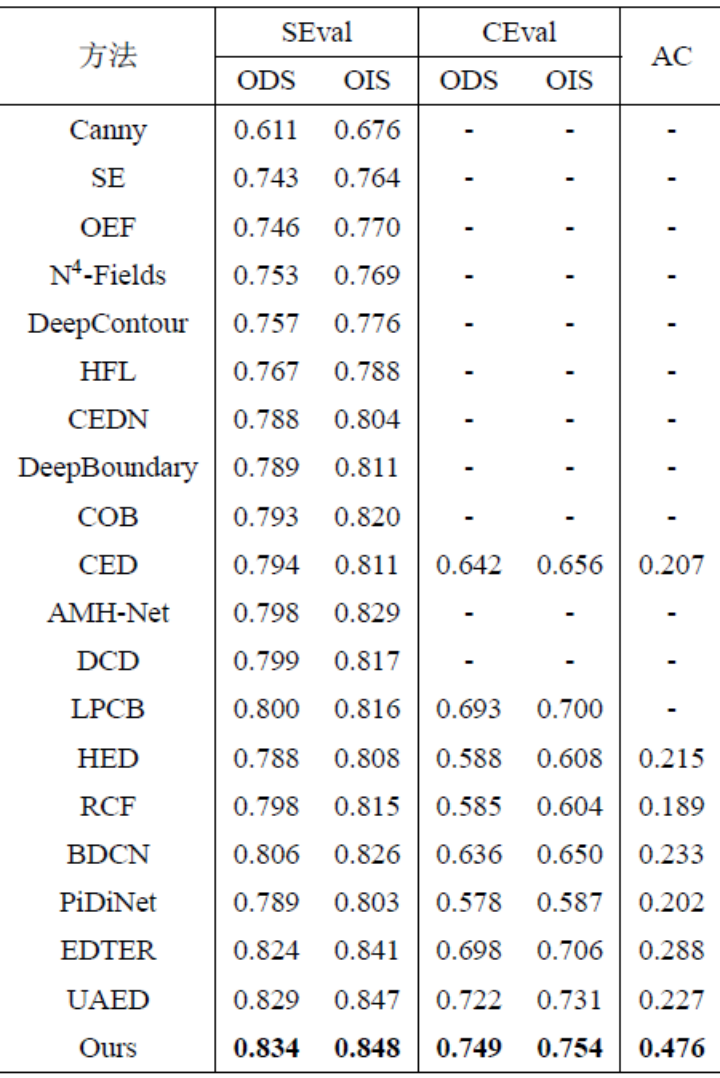
Tableau 2 Comparaison quantitative de différentes méthodes sur l'ensemble de données BSDS 3 Comparaison qualitative de différentes méthodes sur l'ensemble de données BSDS

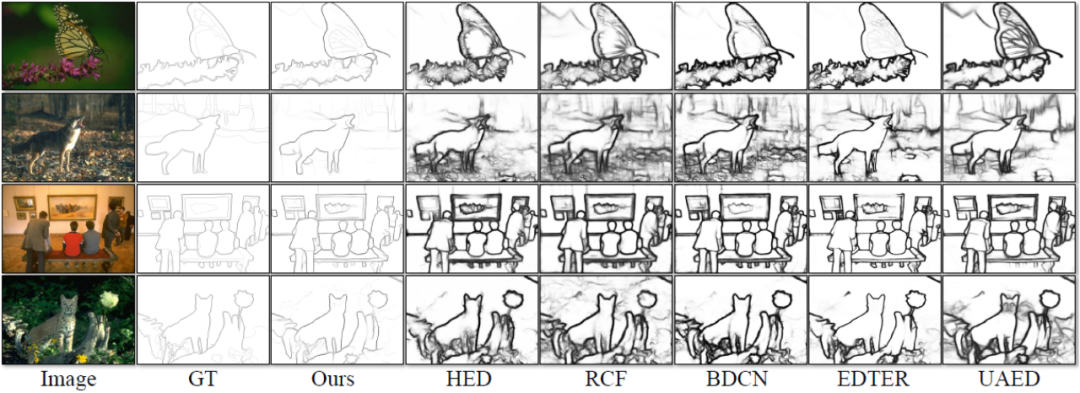
Figure 4 Comparaison qualitative de différentes méthodes sur l'ensemble de données NYUDv2

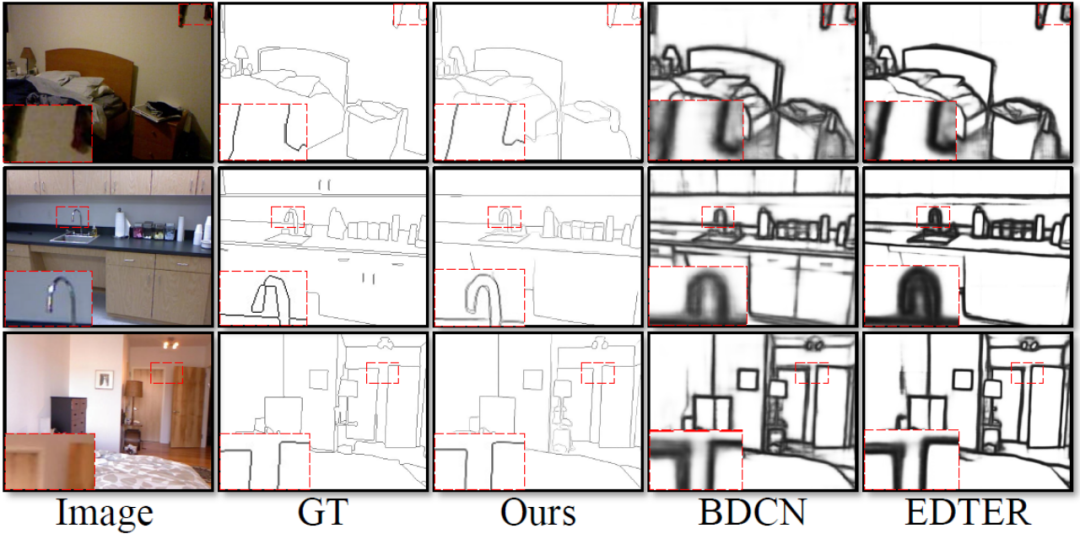
Figure 5 Comparaison qualitative de différentes méthodes sur l'ensemble de données BIPED

Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!