
La réduction de dimensionnalité fait référence à la conservation autant que possible des informations principales des données tout en réduisant le nombre de fonctionnalités dans l'ensemble de données. Les algorithmes de réduction de dimensionnalité sont un apprentissage non supervisé et l'algorithme est formé à partir de données non étiquetées.

Bien qu'il existe de nombreux types de méthodes de réduction de dimensionnalité, elles peuvent toutes être classées en deux grandes catégories : linéaires et non linéaires.
Les méthodes linéaires projettent linéairement les données d'un espace de grande dimension vers un espace de basse dimension (d'où le nom de projection linéaire). Les exemples incluent PCA et LDA.
Les méthodes non linéaires sont un moyen d'effectuer une réduction de dimensionnalité non linéaire, souvent utilisée pour découvrir la structure non linéaire des données originales. Les méthodes de réduction de dimensionnalité non linéaire sont particulièrement importantes lorsque les données originales ne sont pas facilement séparées linéairement. Dans certains cas, la réduction de dimensionnalité non linéaire est également connue sous le nom d'apprentissage multiple. Cette méthode peut gérer plus efficacement les données de grande dimension et aider à révéler la structure sous-jacente des données. Grâce à la réduction de dimensionnalité non linéaire, nous pouvons mieux comprendre la relation entre les données, découvrir des modèles et des règles cachés dans les données et fournir un support solide pour des analyses et des applications de données plus approfondies.
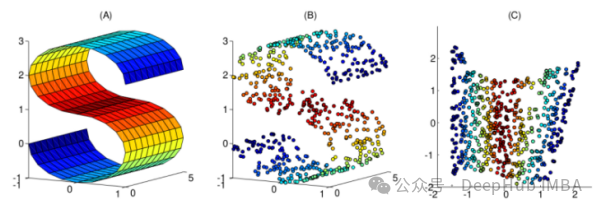
Cet article a compilé 10 techniques de réduction de dimensionnalité non linéaire couramment utilisées pour vous aider à choisir dans votre travail quotidien
Vous connaissez peut-être la PCA normale, qui est une technique de réduction de dimensionnalité linéaire. Kernel PCA peut être considéré comme une version non linéaire de l’analyse normale en composantes principales.
L'analyse en composantes principales et l'analyse en composantes principales du noyau peuvent être utilisées pour la réduction de la dimensionnalité, mais la PCA du noyau est plus efficace dans le traitement des données linéairement inséparables. Le principal avantage du noyau PCA est de transformer des données non linéairement séparables en données linéairement séparables tout en réduisant la dimension des données. Kernel PCA peut capturer la structure non linéaire des données en introduisant des techniques de noyau, améliorant ainsi les performances de classification des données. Par conséquent, le noyau PCA a une plus grande capacité d’expressivité et de généralisation lorsqu’il s’agit d’ensembles de données complexes.
Nous créons d'abord une donnée très classique :
import matplotlib.pyplot as plt plt.figure(figsize=[7, 5]) from sklearn.datasets import make_moons X, y = make_moons(n_samples=100, noise=None, random_state=0) plt.scatter(X[:, 0], X[:, 1], c=y, s=50, cmap='plasma') plt.title('Linearly inseparable data')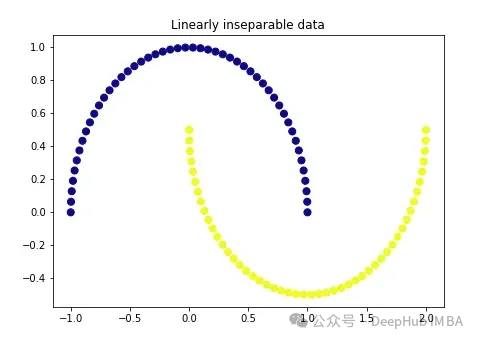
Ces deux couleurs représentent deux catégories linéairement indissociables. Il est impossible de tracer ici une ligne droite pour séparer ces deux catégories.
Nous commençons par un PCA régulier.
import numpy as np from sklearn.decomposition import PCA pca = PCA(n_components=1) X_pca = pca.fit_transform(X) plt.figure(figsize=[7, 5]) plt.scatter(X_pca[:, 0], np.zeros((100,1)), c=y, s=50, cmap='plasma') plt.title('First component after linear PCA') plt.xlabel('PC1')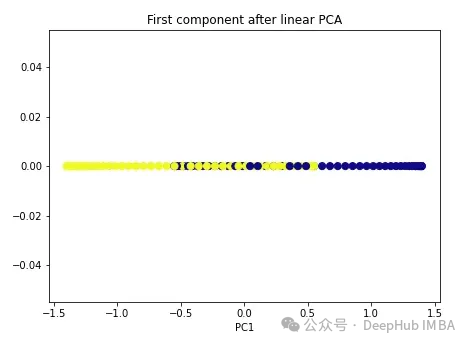
Comme vous pouvez le constater, ces deux classes sont toujours linéairement indissociables, essayons maintenant le noyau PCA.
import numpy as np from sklearn.decomposition import KernelPCA kpca = KernelPCA(n_components=1, kernel='rbf', gamma=15) X_kpca = kpca.fit_transform(X) plt.figure(figsize=[7, 5]) plt.scatter(X_kpca[:, 0], np.zeros((100,1)), c=y, s=50, cmap='plasma') plt.axvline(x=0.0, linestyle='dashed', color='black', linewidth=1.2) plt.title('First component after kernel PCA') plt.xlabel('PC1')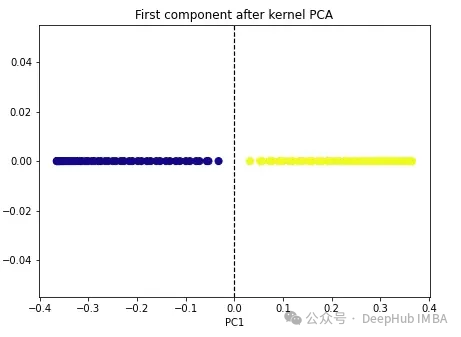
Les deux classes deviennent linéairement séparables et l'algorithme PCA du noyau utilise différents noyaux pour transformer les données d'une forme à une autre. Kernel PCA est un processus en deux étapes. Premièrement, la fonction noyau projette temporairement les données originales dans un espace de grande dimension, où les classes sont linéairement séparables. L'algorithme projette ensuite ces données vers les dimensions inférieures spécifiées dans l'hyperparamètre n_components (le nombre de dimensions que nous souhaitons conserver).
Il existe quatre options de noyau dans sklearn : linéaire", "poly", "rbf" et "sigmoïde". Si nous spécifions le noyau comme "linéaire", une PCA normale sera effectuée. Tout autre noyau effectuera une PCA non linéaire. Le noyau rbf (radial basic function) est le plus couramment utilisé.
La mise à l'échelle multidimensionnelle est une autre technique de réduction de dimensionnalité non linéaire qui effectue une réduction de dimensionnalité en maintenant la distance entre les points de données de haute dimension et de basse dimension. Par exemple, les points qui sont plus proches dans la dimension d'origine apparaissent également plus proches dans la forme dimensionnelle inférieure.
Pour ce faire dans Scikit-learn, nous pouvons utiliser la classe MDS(). Les hyperparamètres
from sklearn.manifold import MDS mds = MDS(n_components, metric) mds_transformed = mds.fit_transform(X)
métriques distinguent deux types d'algorithmes MDS : métriques et non métriques. Si metric=True, exécutez la métrique MDS. Sinon, effectuez un MDS non métrique.
Nous appliquons deux types d'algorithmes MDS aux données non linéaires suivantes.
import numpy as np from sklearn.manifold import MDS mds = MDS(n_components=1, metric=True) # Metric MDS X_mds = mds.fit_transform(X) plt.figure(figsize=[7, 5]) plt.scatter(X_mds[:, 0], np.zeros((100,1)), c=y, s=50, cmap='plasma') plt.title('Metric MDS') plt.xlabel('Component 1')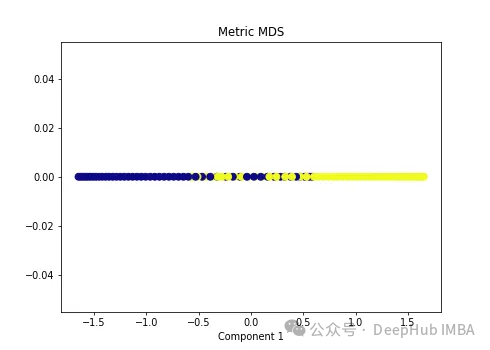
import numpy as np from sklearn.manifold import MDS mds = MDS(n_components=1, metric=False) # Non-metric MDS X_mds = mds.fit_transform(X) plt.figure(figsize=[7, 5]) plt.scatter(X_mds[:, 0], np.zeros((100,1)), c=y, s=50, cmap='plasma') plt.title('Non-metric MDS') plt.xlabel('Component 1')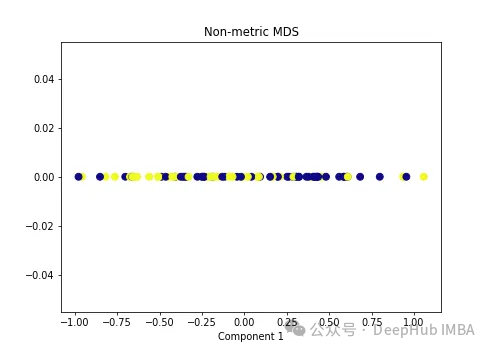
可以看到MDS后都不能使数据线性可分,所以可以说MDS不适合我们这个经典的数据集。
Isomap(Isometric Mapping)在保持数据点之间的地理距离,即在原始高维空间中的测地线距离或者近似的测地线距离,在低维空间中也被保持。Isomap的基本思想是通过在高维空间中计算数据点之间的测地线距离(通过最短路径算法,比如Dijkstra算法),然后在低维空间中保持这些距离来进行降维。在这个过程中,Isomap利用了流形假设,即假设高维数据分布在一个低维流形上。因此,Isomap通常在处理非线性数据集时表现良好,尤其是当数据集包含曲线和流形结构时。
import matplotlib.pyplot as plt plt.figure(figsize=[7, 5]) from sklearn.datasets import make_moons X, y = make_moons(n_samples=100, noise=None, random_state=0) import numpy as np from sklearn.manifold import Isomap isomap = Isomap(n_neighbors=5, n_components=1) X_isomap = isomap.fit_transform(X) plt.figure(figsize=[7, 5]) plt.scatter(X_isomap[:, 0], np.zeros((100,1)), c=y, s=50, cmap='plasma') plt.title('First component after applying Isomap') plt.xlabel('Component 1')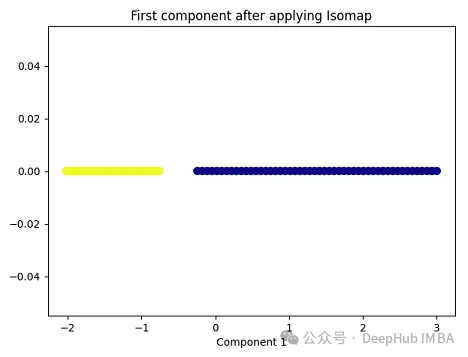
就像核PCA一样,这两个类在应用Isomap后是线性可分的!
与Isomap类似,LLE也是基于流形假设,即假设高维数据分布在一个低维流形上。LLE的主要思想是在局部邻域内保持数据点之间的线性关系,并在低维空间中重构这些关系。
from sklearn.manifold import LocallyLinearEmbedding lle = LocallyLinearEmbedding(n_neighbors=5,n_components=1) lle_transformed = lle.fit_transform(X) plt.figure(figsize=[7, 5]) plt.scatter(lle_transformed[:, 0], np.zeros((100,1)), c=y, s=50, cmap='plasma') plt.title('First component after applying LocallyLinearEmbedding') plt.xlabel('Component 1')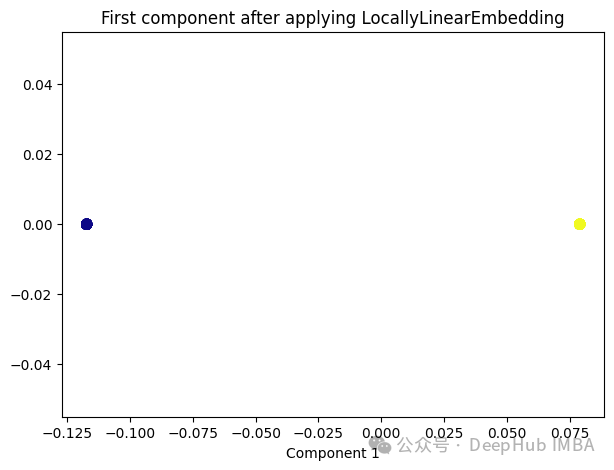
只有2个点,其实并不是这样,我们打印下这个数据
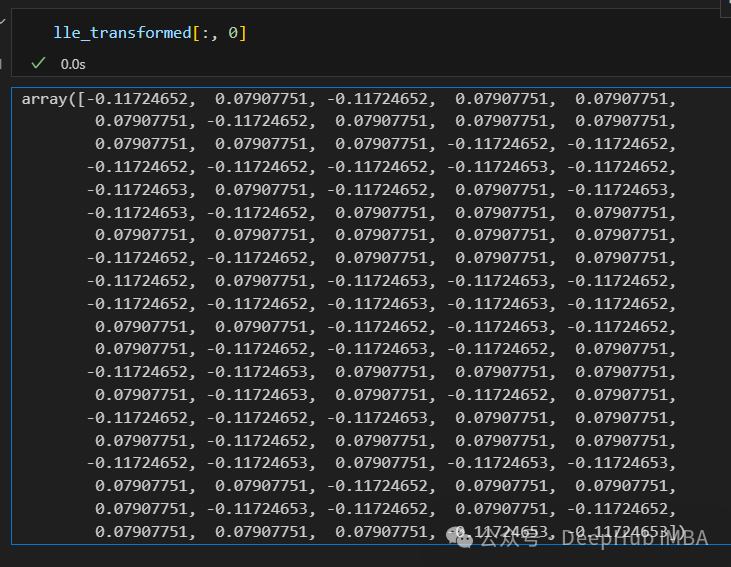
可以看到数据通过降维变成了同一个数字,所以LLE降维后是线性可分的,但是却丢失了数据的信息。
Spectral Embedding是一种基于图论和谱理论的降维技术,通常用于将高维数据映射到低维空间。它的核心思想是利用数据的相似性结构,将数据点表示为图的节点,并通过图的谱分解来获取低维表示。
from sklearn.manifold import SpectralEmbedding sp_emb = SpectralEmbedding(n_components=1, affinity='nearest_neighbors') sp_emb_transformed = sp_emb.fit_transform(X) plt.figure(figsize=[7, 5]) plt.scatter(sp_emb_transformed[:, 0], np.zeros((100,1)), c=y, s=50, cmap='plasma') plt.title('First component after applying SpectralEmbedding') plt.xlabel('Component 1')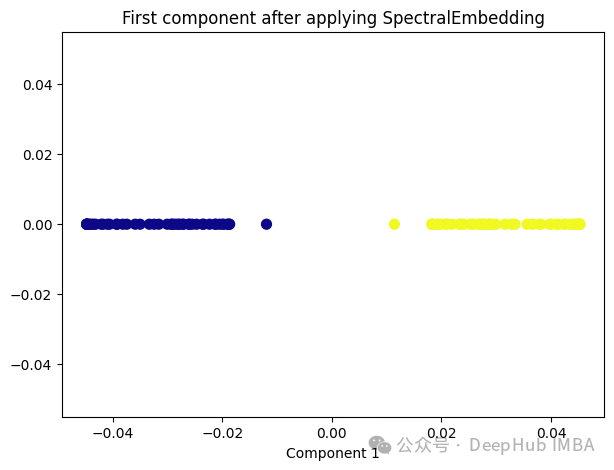
t-SNE的主要目标是保持数据点之间的局部相似性关系,并在低维空间中保持这些关系,同时试图保持全局结构。
from sklearn.manifold import TSNE tsne = TSNE(1, learning_rate='auto', init='pca') tsne_transformed = tsne.fit_transform(X) plt.figure(figsize=[7, 5]) plt.scatter(tsne_transformed[:, 0], np.zeros((100,1)), c=y, s=50, cmap='plasma') plt.title('First component after applying TSNE') plt.xlabel('Component 1')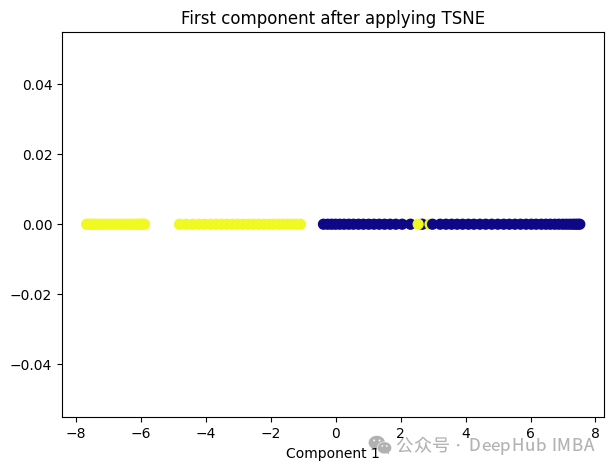
t-SNE好像也不太适合我们的数据。
Random Trees Embedding是一种基于树的降维技术,常用于将高维数据映射到低维空间。它利用了随机森林(Random Forest)的思想,通过构建多棵随机决策树来实现降维。
Random Trees Embedding的基本工作流程:
Random Trees Embedding的优势在于它的计算效率高,特别是对于大规模数据集。由于使用了随机森林的思想,它能够很好地处理高维数据,并且不需要太多的调参过程。
RandomTreesEmbedding使用高维稀疏进行无监督转换,也就是说,我们最终得到的数据并不是一个连续的数值,而是稀疏的表示。所以这里就不进行代码展示了,有兴趣的看看sklearn的sklearn.ensemble.RandomTreesEmbedding
Dictionary Learning是一种用于降维和特征提取的技术,它主要用于处理高维数据。它的目标是学习一个字典,该字典由一组原子(或基向量)组成,这些原子是数据的线性组合。通过学习这样的字典,可以将高维数据表示为一个更紧凑的低维空间中的稀疏线性组合。
Dictionary Learning的优点之一是它能够学习出具有可解释性的原子,这些原子可以提供关于数据结构和特征的重要见解。此外,Dictionary Learning还可以产生稀疏表示,从而提供更紧凑的数据表示,有助于降低存储成本和计算复杂度。
from sklearn.decomposition import DictionaryLearning dict_lr = DictionaryLearning(n_components=1) dict_lr_transformed = dict_lr.fit_transform(X) plt.figure(figsize=[7, 5]) plt.scatter(dict_lr_transformed[:, 0], np.zeros((100,1)), c=y, s=50, cmap='plasma') plt.title('First component after applying DictionaryLearning') plt.xlabel('Component 1')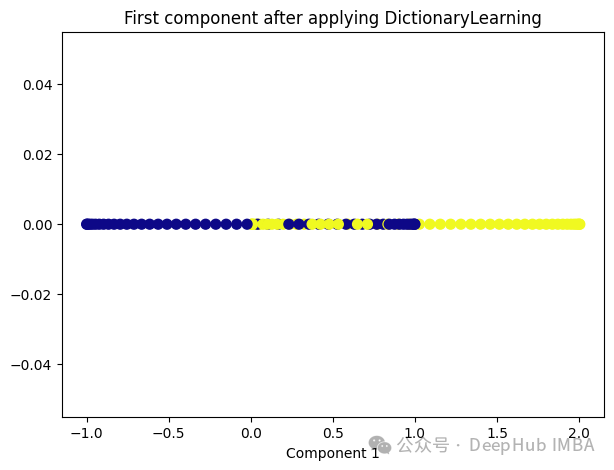
Independent Component Analysis (ICA) 是一种用于盲源分离的统计方法,通常用于从混合信号中估计原始信号。在机器学习和信号处理领域,ICA经常用于解决以下问题:
ICA的基本假设是,混合信号中的各个成分是相互独立的,即它们的统计特性是独立的。这与主成分分析(PCA)不同,PCA假设成分之间是正交的,而不是独立的。因此ICA通常比PCA更适用于发现非高斯分布的独立成分。
from sklearn.decomposition import FastICA ica = FastICA(n_components=1, whiten='unit-variance') ica_transformed = dict_lr.fit_transform(X) plt.figure(figsize=[7, 5]) plt.scatter(ica_transformed[:, 0], np.zeros((100,1)), c=y, s=50, cmap='plasma') plt.title('First component after applying FastICA') plt.xlabel('Component 1')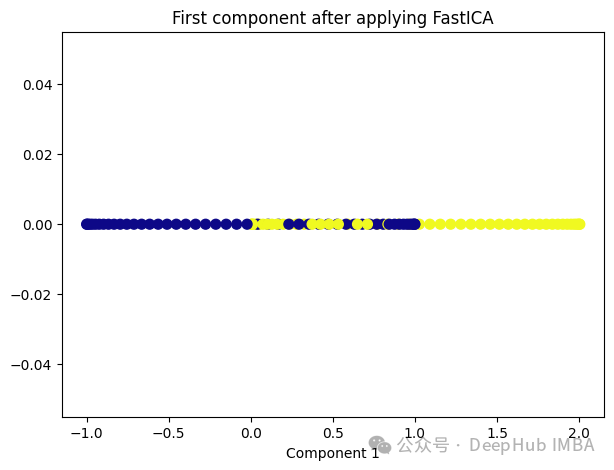
到目前为止,我们讨论的NLDR技术属于通用机器学习算法的范畴。而自编码器是一种基于神经网络的NLDR技术,可以很好地处理大型非线性数据。当数据集较小时,自动编码器的效果可能不是很好。
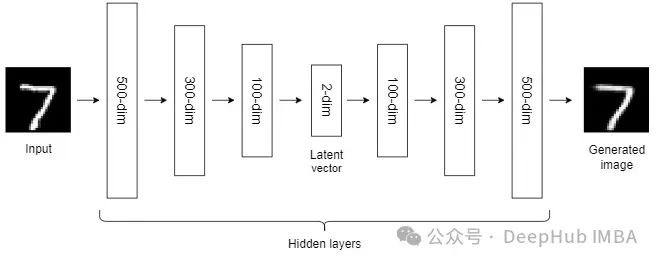
自编码器我们已经介绍过很多次了,所以这里就不详细说明了。
非线性降维技术是一类用于将高维数据映射到低维空间的方法,它们通常适用于数据具有非线性结构的情况。
大多数NLDR方法基于最近邻方法,该方法要求数据中所有特征的尺度相同,所以如果特征的尺度不同,还需要进行缩放。
另外这些非线性降维技术在不同的数据集和任务中可能表现出不同的性能,因此在选择合适的方法时需要考虑数据的特征、降维的目标以及计算资源等因素。
Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!
 Quels types de fichiers peuvent être identifiés sur la base
Quels types de fichiers peuvent être identifiés sur la base
 logiciel erp gratuit
logiciel erp gratuit
 Comment l'Oracle tourne
Comment l'Oracle tourne
 Utilisation de promesse
Utilisation de promesse
 msvcp140.dll
msvcp140.dll
 Quelle est la priorité de l'interruption ?
Quelle est la priorité de l'interruption ?
 Outil de valorisation de nom de domaine de site Web
Outil de valorisation de nom de domaine de site Web
 winkawaksrom
winkawaksrom
 Les pièces d'inscription Sols reviendront-elles à zéro ?
Les pièces d'inscription Sols reviendront-elles à zéro ?