
Nous pouvons voir que la file d'attente et la pile dans le concept JavaScript sont à la fois une structure de liste linéaire spéciale et une structure de stockage séquentielle relativement simple basée sur un tableau. Étant donné que l'interpréteur JavaScript a été directement optimisé pour les tableaux, il n'y aura pas de problème de longueur fixe des tableaux dans de nombreux langages de programmation (il est plus difficile d'ajouter une fois le tableau plein, y compris l'ajout et la suppression, tous doivent être dans le tableau) Tous les éléments changent de position, et les tableaux JavaScript sont en effet directement optimisés, comme les méthodes push, pop, shift, unshift, split, etc...)
Le plus gros inconvénient de la structure de stockage séquentielle d'une table linéaire est que la modification de la disposition de l'un des éléments entraînera des modifications dans l'ensemble de la collection. La raison en est que le stockage dans la mémoire est intrinsèquement cohérent et ne comporte aucune lacune. La suppression d'un élément compensera naturellement. Après l'optimisation de cette structure, la structure de stockage en chaîne est apparue. Pour changer la façon de penser, nous ne nous soucions pas du tout de la disposition des données, il suffit d'enregistrer la position des données suivantes à l'intérieur de chaque élément, donc. utilisation La liste linéaire stockée en mode lien est appelée liste chaînée en abrégé Dans la structure liée, data = (adresse d'information)
.Dans la structure de la chaîne, on peut aussi appeler l'adresse une "chaîne". Une unité de données est un nœud, on peut donc dire que la liste chaînée est une collection de nœuds. Chaque nœud a une référence de bloc de données pointant vers son nœud suivant
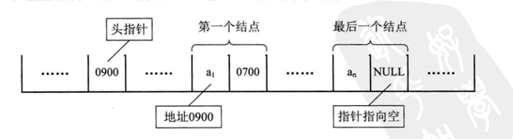
Les éléments du tableau sont référencés logiquement en fonction de relations de position, tandis que les listes chaînées sont référencées en fonction de chaque élément de données enregistrant une relation de pointeur de référence
Les avantages de cette structure sont très évidents. Lors de l'insertion d'une donnée, vous n'avez pas du tout à vous soucier de sa disposition, il vous suffit de relier les directions de la "chaîne"
.L'idée de listes chaînées de cette manière ne se limite pas aux tableaux, nous pouvons utiliser des objets, tant qu'il existe une relation de référence entre les objets
Les pistes incluent généralement des listes chaînées simples, des listes chaînées statiques, des listes chaînées circulaires et des listes doublement chaînées
Liste chaînée unique : il s'agit d'une transmission descendante très simple. Chaque nœud n'enregistre que les informations du nœud suivant. Tout comme Tony Leung dans Infernal Affairs, l'agent infiltré communique avec le système en ligne et hors ligne via un intermédiaire. est coupé, alors je ne peux pas prouver mon identité, donc il y a une phrase à la fin du film : "Je suis une bonne personne, qui sait
Liste chaînée statique : C'est une liste chaînée décrite par un tableau. Autrement dit, chaque table du tableau est une "section" contenant des données et des pointeurs
Liste chaînée circulaire : étant donné que la liste chaînée unique ne sera transmise que vers l'arrière, une fois arrivée à la fin, il sera très difficile de revenir à la tête, donc la chaîne de la section de queue est connectée à la tête pour former une boucle
Liste chaînée double : optimisation pour la liste chaînée unique, afin que chaque section puisse savoir qui est avant et après, donc en plus du champ de pointeur arrière, il y aura également un champ de pointeur avant, ce qui améliore l'efficacité de la recherche, mais pose quelques problèmes de conception. D'une manière générale, la complexité est d'échanger l'espace contre le temps
Pour résumer, en fait, la liste chaînée est une méthode d'optimisation de la structure de stockage séquentielle dans la liste linéaire. Cependant, dans le langage JavaScript, du fait de la particularité du tableau (mise à jour automatique de la position de référence), nous peut utiliser des objets pour stocker la liste chaînée
.Liste chaînée unique
Nous mettons en œuvre la relation de liste chaînée la plus simple
function createLinkList() {
var _this = {},
prev = null;
return {
add: function(val) {
//保存当前的引用
prev = {
data: val,
next: prev || null
}
}
}
}
var linksList = createLinkList();
linksList.add("arron1");
linksList.add("arron2");
linksList.add("arron3");
//node节的next链就是 -arron3-arron2-arron1Se référer directement à l'objet nœud suivant via le prochain objet nœud. Initialement, la référence via la liste chaînée est implémentée dans la méthode then dans le différé asynchrone de jQuery et dans le jsderferre du cho45 du Japon. . Il existe un autre problème très critique dans cette implémentation. Comment insérer dynamiquement des données après la section exécutée ?
Nous devons donc concevoir une méthode de parcours pour rechercher les données sur cette chaîne de nœuds, puis trouver les données correspondantes, insérer la nouvelle section dans la chaîne actuelle et réécrire l'enregistrement de localisation
//在链表中找到对应的节
var findNode = function createFindNode(currNode) {
return function(key){
//循环找到执行的节,如果没有返回本身
while (currNode.data != key) {
currNode = currNode.next;
}
return currNode;
}
}(headNode);Il s'agit d'une méthode pour trouver la section actuelle, en passant la section head headNode d'origine pour rechercher ensuite jusqu'à ce que les informations de la section correspondante soient trouvées
Ceci est mis en œuvre en utilisant la méthode du curry
Ensuite, lors de l'insertion d'une section, la relation de conversion pour l'adresse de la liste chaînée est la suivante
Dans la liste chaînée de a-b-c-d, si vous souhaitez insérer un f
après c(c.next->d)a-b-c-f-d , puis c,next->f , f.next-d
Ajouter une section via la méthode d'insertion
//创建节
function createNode(data) {
this.data = data;
this.next = null;
}
//初始化头部节
//从headNode开始形成一条链条
//通过next衔接
var headNode = new createNode("head");
//在链表中找到对应的节
var findNode = function createFindNode(currNode) {
return function(key){
//循环找到执行的节,如果没有返回本身
while (currNode.data != key) {
currNode = currNode.next;
}
return currNode;
}
}(headNode);
//插入一个新节
this.insert = function(data, key) {
//创建一个新节
var newNode = new createNode(data);
//在链条中找到对应的数据节
//然后把新加入的挂进去
var current = findNode(key);
//插入新的接,更改引用关系
//1:a-b-c-d
//2:a-b-n-c-d
newNode.next = current.next;
current.next = newNode;
};
首先分离出createNode节的构建,在初始化的时候先创建一个头部节对象用来做节开头的初始化对象
在insert增加节方法中,通过对headNode链的一个查找,找到对应的节,把新的节给加后之后,最后就是修改一下链的关系
如何从链表中删除一个节点?
由于链表的特殊性,我们a->b->c->d ,如果要删除c那么就必须修改b.next->c为 b.next->d,所以找到前一个节修改其链表next地址,这个有点像dom操作中removeChild找到其父节点调用移除子节点
同样的我们也在remove方法的设计中,需要设计一个遍历往上回溯一个父节点即可
//找到前一个节
var findPrevious = function(currNode) {
return function(key){
while (!(currNode.next == null) &&
(currNode.next.data != key)) {
currNode = currNode.next;
}
return currNode;
}
}(headNode);
//插入方法
this.remove = function(key) {
var prevNode = findPrevious(key);
if (!(prevNode.next == null)) {
//修改链表关系
prevNode.next = prevNode.next.next;
}
};
测试代码:
<!doctype html><button id="test1">插入多条数据</button>
<button id="test2">删除Russellville数据</button><div id="listshow"><br /></div><script type="text/javascript">
//////////
//创建链表 //
//////////
function createLinkList() {
//创建节
function createNode(data) {
this.data = data;
this.next = null;
}
//初始化头部节
//从headNode开始形成一条链条
//通过next衔接
var headNode = new createNode("head");
//在链表中找到对应的节
var findNode = function createFindNode(currNode) {
return function(key) {
//循环找到执行的节,如果没有返回本身
while (currNode.data != key) {
currNode = currNode.next;
}
return currNode;
}
}(headNode);
//找到前一个节
var findPrevious = function(currNode) {
return function(key) {
while (!(currNode.next == null) &&
(currNode.next.data != key)) {
currNode = currNode.next;
}
return currNode;
}
}(headNode);
//插入一个新节
this.insert = function(data, key) {
//创建一个新节
var newNode = new createNode(data);
//在链条中找到对应的数据节
//然后把新加入的挂进去
var current = findNode(key);
//插入新的接,更改引用关系
//1:a-b-c-d
//2:a-b-n-c-d
newNode.next = current.next;
current.next = newNode;
};
//插入方法
this.remove = function(key) {
var prevNode = findPrevious(key);
if (!(prevNode.next == null)) {
//修改链表关系
prevNode.next = prevNode.next.next;
}
};
this.display = function(fn) {
var currNode = headNode;
while (!(currNode.next == null)) {
currNode = currNode.next;
fn(currNode.data)
}
};
}
var cities = new createLinkList();
function create() {
var text = '';
cities.display(function(data) {
text += '-' + data;
});
var div = document.createElement('div')
div.innerHTML = text;
document.getElementById("listshow").appendChild(div)
}
document.getElementById("test1").onclick = function() {
cities.insert("Conway", "head");
cities.insert("Russellville", "Conway");
cities.insert("Carlisle", "Russellville");
cities.insert("Alma", "Carlisle");
create();
}
document.getElementById("test2").onclick = function() {
cities.remove("Russellville");
create()
}
</script>
双链表
原理跟单链表是一样的,无非就是给每一个节增加一个前链表的指针
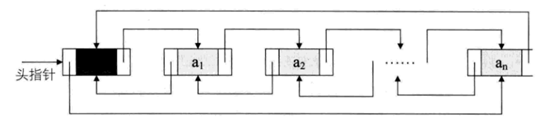
增加节
//插入一个新节
this.insert = function(data, key) {
//创建一个新节
var newNode = new createNode(data);
//在链条中找到对应的数据节
//然后把新加入的挂进去
var current = findNode(headNode,key);
//插入新的接,更改引用关系
newNode.next = current.next;
newNode.previous = current
current.next = newNode;
};
删除节
this.remove = function(key) {
var currNode = findNode(headNode,key);
if (!(currNode.next == null)) {
currNode.previous.next = currNode.next;
currNode.next.previous = currNode.previous;
currNode.next = null;
currNode.previous = null;
}
};在删除操作中有一个明显的优化:不需要找到父节了,因为双链表的双向引用所以效率比单链要高
测试代码:
<!doctype html><button id="test1">插入多条数据</button>
<button id="test2">删除Russellville数据</button><div id="listshow"><br /></div><script type="text/javascript">
//////////
//创建链表 //
//////////
function createLinkList() {
//创建节
function createNode(data) {
this.data = data;
this.next = null;
this.previous = null
}
//初始化头部节
//从headNode开始形成一条链条
//通过next衔接
var headNode = new createNode("head");
//在链表中找到对应的数据
var findNode = function(currNode, key) {
//循环找到执行的节,如果没有返回本身
while (currNode.data != key) {
currNode = currNode.next;
}
return currNode;
}
//插入一个新节
this.insert = function(data, key) {
//创建一个新节
var newNode = new createNode(data);
//在链条中找到对应的数据节
//然后把新加入的挂进去
var current = findNode(headNode,key);
//插入新的接,更改引用关系
newNode.next = current.next;
newNode.previous = current
current.next = newNode;
};
this.remove = function(key) {
var currNode = findNode(headNode,key);
if (!(currNode.next == null)) {
currNode.previous.next = currNode.next;
currNode.next.previous = currNode.previous;
currNode.next = null;
currNode.previous = null;
}
};
this.display = function(fn) {
var currNode = headNode;
while (!(currNode.next == null)) {
currNode = currNode.next;
fn(currNode.data)
}
};
}
var cities = new createLinkList();
function create() {
var text = '';
cities.display(function(data) {
text += '-' + data;
});
var div = document.createElement('div')
div.innerHTML = text;
document.getElementById("listshow").appendChild(div)
}
document.getElementById("test1").onclick = function() {
cities.insert("Conway", "head");
cities.insert("Russellville", "Conway");
cities.insert("Carlisle", "Russellville");
cities.insert("Alma", "Carlisle");
create();
}
document.getElementById("test2").onclick = function() {
cities.remove("Russellville");
create()
}
</script>