En éliminant les « inefficacités cachées », les informaticiens ont mis au point une nouvelle façon de multiplier de grandes matrices plus rapidement que jamais.
En tant qu'opération de base de nombreux opérateurs GPU, la multiplication matricielle joue un rôle important dans le calcul haute performance et est également un élément clé d'applications telles que l'IA. Bien que l’algorithme lui-même soit relativement simple, des efforts ont été déployés pour l’optimiser au fil des années afin d’atteindre des vitesses plus élevées. Cependant, le degré d'optimisation a été quelque peu limité.
Dans le dernier numéro de Quantum Magazine, nous avons trouvé deux articles qui peuvent accélérer la multiplication matricielle. Un étudiant de premier cycle de la classe Yao de l'Université Tsinghua a participé activement à la rédaction de ces deux articles, ce qui a ouvert de nouvelles perspectives d'amélioration des algorithmes dans ce domaine.
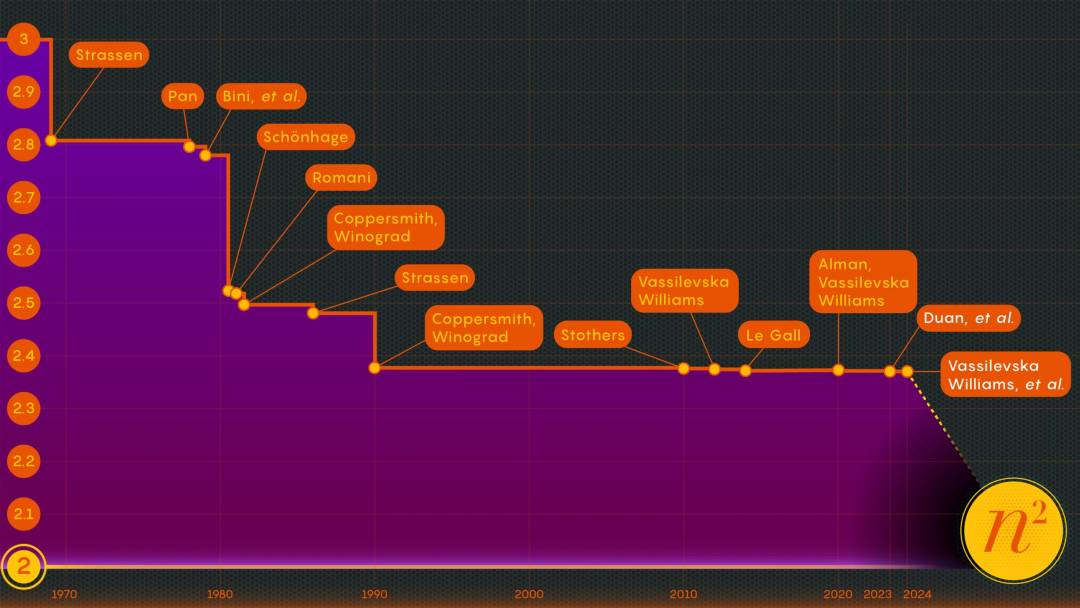
Une nouvelle "singularité" apparaît dans l'amélioration de la multiplication matricielle
Les informaticiens sont un groupe de personnes très exigeants. Leur objectif n’est pas seulement de résoudre des problèmes, mais également d’atteindre leurs objectifs de la manière la plus efficace possible.
Prenons l'exemple de la multiplication de matrices ou de tableaux de nombres. En 1812, le mathématicien français Jacques Philippe Marie Binet a proposé un ensemble de règles de base qui sont encore enseignées aux étudiants aujourd'hui. Cet ensemble de règles est largement utilisé, mais ces dernières années, certains mathématiciens ont découvert des moyens de simplifier et d'accélérer le processus. Mathématicien français Jacques Philippe Marie Binet.
Ran Duan et Renfei Zhou de l'Université Tsinghua et de Hongxun Wu de l'Université de Californie à Berkeley pour résoudre ce problème de longue date. réalisés, et les résultats de leurs recherches sont présentés en détail dans un article de 87 pages. Le Gall a fait l'éloge du travail de ces trois chercheurs. Il estime que, même si l'amélioration est relativement faible, il s'agit d'une avancée conceptuelle sans précédent. Cet article a été accepté par FOCS 2023, la plus grande conférence dans le domaine de l'informatique.
Paper v1 sortira en octobre 2022, la v5 en novembre 2023. Adresse de l'article : https://arxiv.org/abs/2210.10173
Parmi eux, Duan Ran est professeur agrégé à l'Institut d'information croisée de l'Université Tsinghua. Ses principaux domaines de recherche sont les algorithmes de théorie des graphes, les structures de données et l'informatique. théorie. Hongxun Wu est doctorant en deuxième année à l'Université de Californie à Berkeley et diplômé de la classe Yao de l'Université Tsinghua.
L'article de trois chercheurs révèle des sources potentielles d'amélioration jusqu'alors inconnues et inexploitées qui portent déjà leurs fruits. Un deuxième article publié en janvier 2024 (également co-écrit par Renfei Zhou) s'appuie sur ce point et montre comment la multiplication matricielle peut être encore améliorée.
Adresse papier : https://epubs.siam.org/doi/10.1137/1.9781611977912.134William Kuszmaul, informaticien théoricien à l'Université Harvard, a déclaré qu'il s'agissait d'une avancée technologique majeure, plus de dix La plus grande amélioration que nous ayons vue depuis des années pour la multiplication matricielle.
Quel problème devrait être amélioré dans la multiplication matricielleLa multiplication matricielle peut sembler un problème obscur, mais il s'agit d'une opération informatique de base. Il est intégré à la plupart des algorithmes que les gens utilisent quotidiennement pour diverses tâches, depuis l'affichage d'infographies plus claires jusqu'à la résolution de problèmes logistiques dans la théorie des réseaux. Tout comme dans d’autres domaines de l’informatique, la vitesse est essentielle. Même de petites améliorations pourraient à terme réduire considérablement le temps, la puissance de calcul et l’argent nécessaires. Mais pour l’instant, les théoriciens s’intéressent principalement à la rapidité avec laquelle le processus peut se dérouler.
La méthode traditionnelle de multiplication de deux matrices n×n, c'est-à-dire multiplier les nombres de chaque ligne de la première matrice par les nombres de chaque colonne de la deuxième matrice, nécessite n³ opérations de multiplication indépendantes. Pour une matrice 2 par 2, cela signifie 2³, soit 8 multiplications.
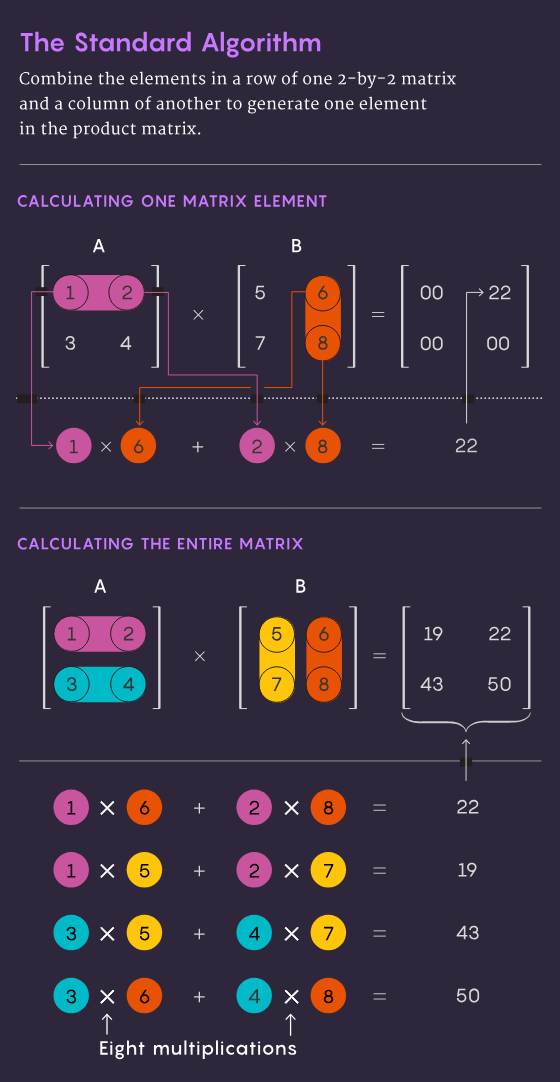
En 1969, le mathématicien Volker Strassen a découvert une méthode plus élégante permettant de réaliser la multiplication de matrices 2×2 en seulement 7 étapes de multiplication et 18 étapes d'addition. Deux ans plus tard, l’informaticien Shmuel Winograd démontrait que la multiplication en 7 étapes était bien le minimum absolu pour une matrice 2×2.
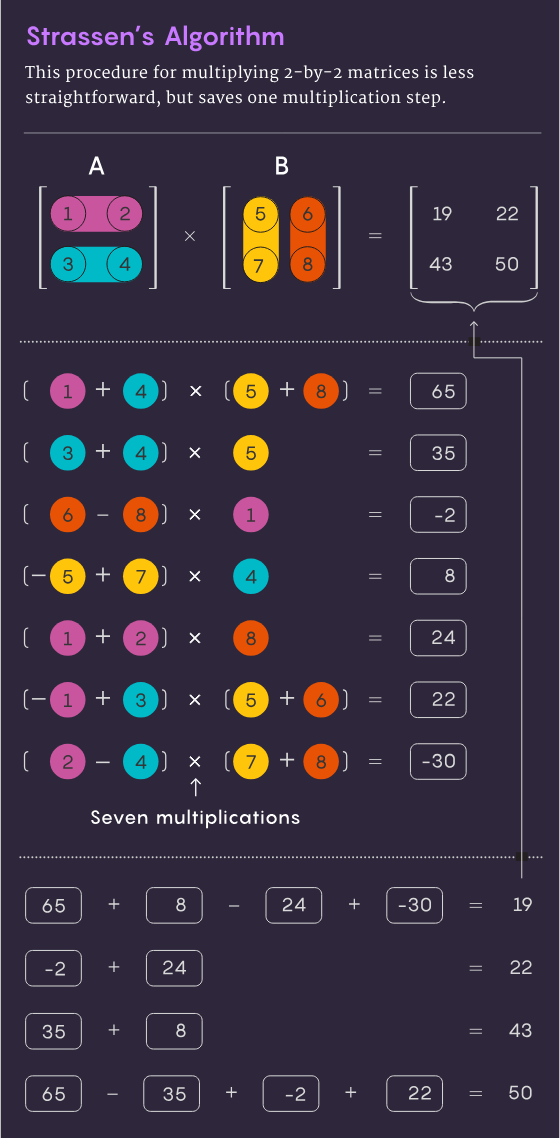
Strassen a utilisé la même idée pour montrer que toutes les matrices n×n plus grandes peuvent également être multipliées en moins de n3 étapes. Un élément clé de cette stratégie implique une procédure appelée décomposition : décomposer une grande matrice en sous-matrices plus petites, qui peuvent finir par être aussi petites que 2×2 ou même 1×1 (juste un seul nombre).
La raison pour laquelle on divise des tableaux géants en petits morceaux est assez simple, Virginia Vassilevska Williams, informaticienne au MIT, a déclaré : « Pour une grande matrice (comme une matrice 100×100), il est difficile pour les humains d'y penser. le meilleur algorithme. » Même la matrice 3 par 3 n’est pas encore complètement résolue. "Cependant, on peut utiliser des algorithmes rapides développés pour de petites matrices pour obtenir des algorithmes rapides pour des matrices plus grandes."
Les chercheurs ont déterminé que la clé de la vitesse est de réduire le nombre d'étapes de multiplication, en déplaçant autant l'exposant de n3. autant que possible (méthode traditionnelle) réduire. La valeur n² la plus basse possible correspond essentiellement au temps nécessaire pour rédiger la réponse. Les informaticiens appellent cet exposant Ω, ou ω. nω est le nombre minimum d'étapes nécessaires pour réussir à multiplier deux matrices n×n à mesure que n grandit. Zhou Renfei, qui est également co-auteur de l'article de janvier 2024, a déclaré : « L'objectif de ce travail est de voir à quel point vous pouvez vous rapprocher de 2 et si cela peut être atteint théoriquement
Méthode laser
. »En 1986, Strassen a obtenu une autre avancée majeure lorsqu'il a introduit la méthode laser de multiplication matricielle. Strassen a utilisé cela pour déterminer une valeur limite supérieure pour ω de 2,48. Bien que la méthode ne soit qu’une étape dans la multiplication matricielle à grande échelle, elle est l’une des plus importantes car les chercheurs l’améliorent constamment.
Un an plus tard, Winograd et Don Coppersmith introduisent un nouvel algorithme qui complète parfaitement la méthode laser. Cette combinaison d’outils a été utilisée dans presque toutes les recherches ultérieures sur l’accélération de la multiplication matricielle.
Voici une manière simplifiée de voir comment ces différents éléments s’articulent. Commençons par deux grandes matrices A et B et multiplions-les. Tout d’abord, vous les divisez en plusieurs sous-matrices plus petites, parfois appelées blocs. Ensuite, vous pouvez utiliser les algorithmes de Coppersmith et Winograd comme guide pour le traitement et finalement l'assemblage de ces blocs. "Cela me dit quoi multiplier, quoi ajouter et quels éléments se trouvent à quel endroit dans la matrice du produit C", a déclaré Vassilevska Williams. "C'est juste une" recette "pour construire C à partir de A et B."
Cependant, il y a un problème : parfois vous obtenez des blocs avec des éléments communs. Conserver ces éléments communs équivaudrait à compter ces éléments deux fois, donc à un moment donné, ces chevauchements doivent être éliminés. Les chercheurs ont résolu ce problème en « tuant » les blocs dans lesquels ils se trouvaient – en mettant leurs composants à zéro pour les supprimer du calcul. # Virginia Vassilevska Williams fait partie des membres de l'équipe qui ont amélioré la nouvelle méthode de multiplication matricielle, et elle est venue avec la méthode la plus rapide actuellement.
La combinaison de ces différentes techniques aboutit à un algorithme qui multiplie deux matrices avec le moins de multiplications totales possible, du moins en théorie. La méthode laser n’est pas destinée à des applications pratiques ; c’est simplement une façon idéale de penser la multiplication matricielle. Zhou Renfei a déclaré : « Nous n'avons jamais appliqué cette méthode sur un ordinateur, nous l'analysons. » C'est cette analyse qui a contribué à la plus grande amélioration de ω depuis plus de dix ans.
La « perte cachée » découverteDans le premier article « Multiplication matricielle plus rapide via un hachage asymétrique » de Duan Ran, Zhou Renfei et Hongxun Wu, ils ont montré que le processus de l'algorithme de Strassen peut être considérablement accéléré. Tout cela est dû à un concept qu’ils appellent « perte cachée ». Zhou Renfei a déclaré que le concept était profondément caché dans l'analyse précédente et était le résultat de l'élimination par inadvertance d'un trop grand nombre de blocs.
La méthode laser fonctionne en marquant les blocs qui se chevauchent comme des déchets et en planifiant leur traitement, tandis que les autres blocs sont considérés comme précieux et seront sauvegardés. Cependant, le processus de sélection est quelque peu aléatoire. En fait, les blocs marqués comme étant des déchets peuvent finir par être utiles.
Ce n’est pas tout à fait surprenant, mais en examinant de nombreuses sélections aléatoires, l’équipe de Duan Ran a déterminé que la méthode laser sous-estime systématiquement la valeur des blocs, donc plus de blocs devraient être conservés et moins jetés. Et comme c’est souvent le cas, moins de gaspillage se traduit par une plus grande efficacité.
Concernant l'approche de l'équipe de Duan Ran, Le Gall estime que « plus de blocs peuvent être conservés sans se chevaucher.
Après avoir prouvé l'existence de cette perte, l'équipe de Duan Ran a modifié la façon dont le laser. La méthode marque les blocs, réduisant considérablement les déchets. Ils ont fixé un nouveau plafond sur ω autour de 2,371866, ce qui représente une amélioration par rapport au plafond de 2,3728596 fixé par Josh Alman et Vassilevska Williams en 2020.
Cela peut sembler un petit changement,
abaisser la limite supérieure d'environ 0,001, mais c'est la plus grande amélioration que les scientifiques aient vue depuis 2010. En comparaison, les résultats de Vassilevska Williams et Alman en 2020 ne se sont améliorés que de 0,00001 par rapport à leurs résultats précédents.
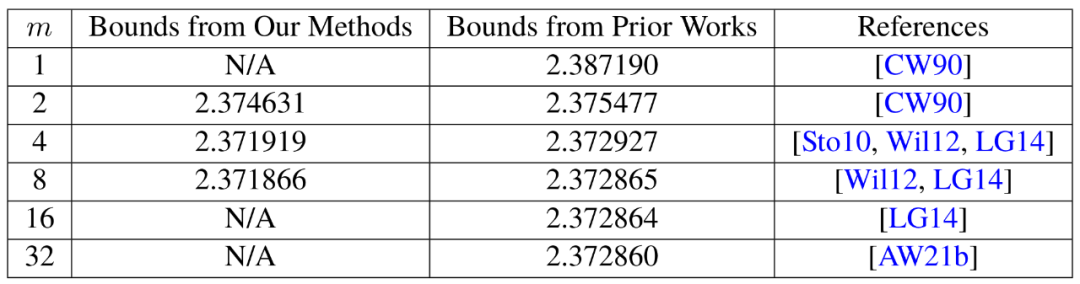Bien sûr, la chose la plus excitante pour les chercheurs n'était pas seulement le nouveau record lui-même, qui n'a pas duré longtemps. En fait, cet article révèle une nouvelle piste d’amélioration qui était auparavant complètement inaperçue. Selon Le Gall, tout le monde s'appuie sur la même méthode laser depuis près de quatre décennies. Avec l’émergence des articles de trois chercheurs, dont Duan Ran, nous pouvons faire mieux.
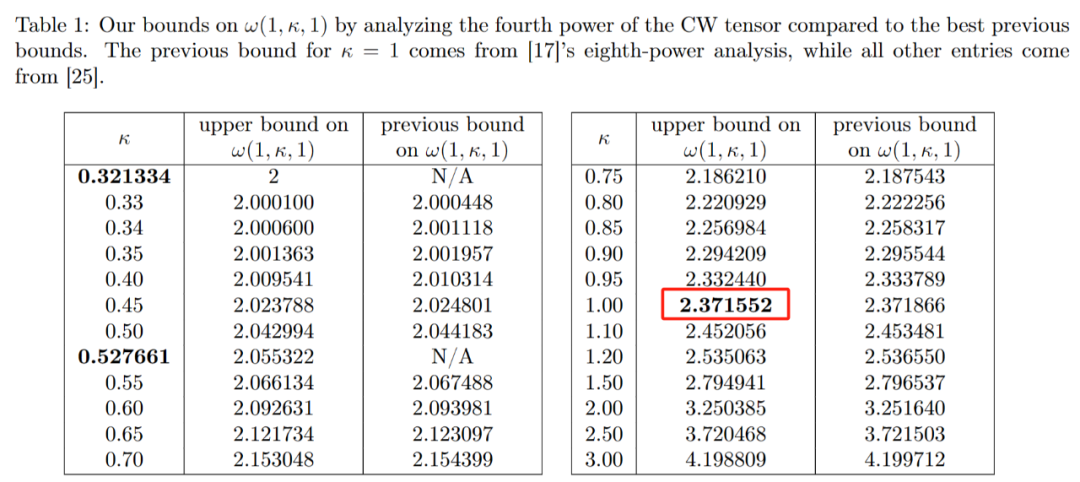
Par conséquent, l'article de janvier 2024 co-écrit par Zhou Renfei a amélioré cette nouvelle méthode et réduit encore les pertes cachées. Ils ont encore augmenté la limite supérieure de ω, la ramenant à 2,371552
.
Lien original :
https://www.quantamagazine.org/new-breakthrough-brings-matrix-multiplication-closer-to-ideal-20240307/
Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!
Utilisation de la fonction accepter
Comment fonctionne la poignée de main TCP à trois voies
Comment résoudre le problème de l'échec du chargement de la DLL
Comment enregistrer des images dans la zone de commentaires Douyin sur un téléphone mobile
Que sont les bibliothèques d'intelligence artificielle Python ?
Comment définir la police en CSS
Objectif principal du système de fichiers
Temps de panne du service Windows 10
![[Web front-end] Démarrage rapide de Node.js](https://img.php.cn/upload/course/000/000/067/662b5d34ba7c0227.png)
