 Périphériques technologiques
Périphériques technologiques
 IA
IA
 L'IA bouleverse la recherche mathématique ! Le lauréat de la médaille Fields et mathématicien sino-américain a dirigé 11 articles les mieux classés | Aimé par Terence Tao
L'IA bouleverse la recherche mathématique ! Le lauréat de la médaille Fields et mathématicien sino-américain a dirigé 11 articles les mieux classés | Aimé par Terence Tao
L'IA bouleverse la recherche mathématique ! Le lauréat de la médaille Fields et mathématicien sino-américain a dirigé 11 articles les mieux classés | Aimé par Terence Tao
L’IA change effectivement les mathématiques.
Récemment, Terence Tao, qui a porté une attention particulière à cette question, a transmis le dernier numéro du "Bulletin of the American Mathematical Society".
Autour du thème "Les machines changeront-elles les mathématiques ?", de nombreux mathématiciens ont exprimé leurs opinions. L'ensemble du processus a été plein d'étincelles, hardcore et passionnant.
L'auteur dispose d'une équipe solide, comprenant le lauréat de la médaille Fields Akshay Venkatesh, le mathématicien chinois Lejun Zheng, l'informaticien de l'Université de New York Ernest Davis et de nombreux autres universitaires bien connus du secteur.

Le monde de l'IA a subi des changements bouleversants. Vous savez, beaucoup de ces articles ont été soumis il y a un an, et au cours de cette année, l'IA a subi de nombreux changements importants.
Cependant, malgré cela, ces articles sont toujours pleins d'or, et ont même fait crier Terence Tao : Ce domaine avance trop vite ! Cela rend mes articles inédits redondants.
Personne ne peut nier que les outils d’IA font progresser le domaine des mathématiques à un rythme alarmant.
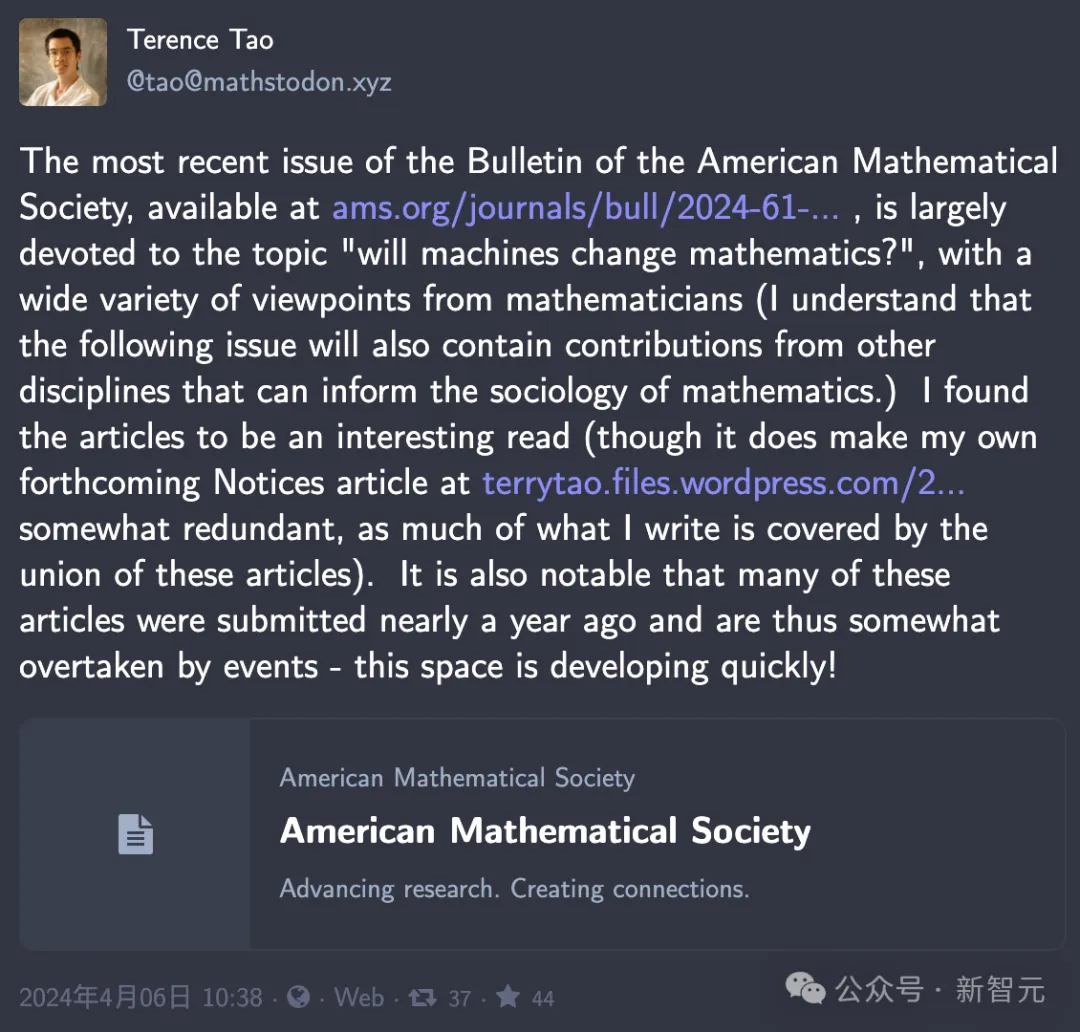
L'intelligence artificielle mènera-t-elle à une révolution dans la manière dont les informations sont collectées et traitées dans les domaines scientifiques, y compris les mathématiques pures ? Est-ce que cela va changer la façon dont les mathématiques sont faites ?
Les mathématiciens sont divisés : certains pensent que l'utilisation généralisée de l'apprentissage automatique dans la recherche est imminente, tandis que d'autres sont sceptiques, rappelant l'optimisme excessif et l'« hiver de l'IA » qui a suivi.
Cependant, des changements drastiques sont très susceptibles de se produire dans la pratique de la recherche mathématique. Il est désormais temps pour les mathématiciens de réfléchir aux problèmes que posent ces changements.
Pas de doute, la tempête est à venir.
Alors, les machines vont-elles changer les mathématiques ?
L'impact de l'automatisation mathématique sur la recherche mathématique
Dans cet article, Akshay Venkatesh, lauréat de la médaille Fields, explore l'impact de l'automatisation sur la recherche mathématique.

Adresse papier : https://www.ams.org/journals/bull/2024-61-02/S0273-0979-2024-01834-5/S0273-0979-2024-01834-5. pdf

Dans cet article, Akshay Venkatesh a proposé une expérience de pensée intéressante :
En 2017, Alphazero de DeepMind a appris tout seul les échecs et le jeu du jour au lendemain, surpassant les humains.
Et si dix ans plus tard, "Alephzero" (écrit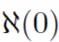 ) faisait aussi les mêmes mathématiques formatées ?
) faisait aussi les mêmes mathématiques formatées ?
Les « mathématiques » dans cet article font référence à la « recherche mathématique pure ».
Notre point de départ est de supposer que "Alephzero" a appris lui-même les mathématiques au lycée et à l'université et a complété tous les exercices de la série SpringerVerlag Graduate Terts in Mathematics. Le lendemain matin, les mathématiciens l'ont publié, les enfants l'ont téléchargé et l'ont exécuté avec nos ressources informatiques.
Il s'agit bien d'une expérience de pensée car manifestement irréaliste : en limitant nos horizons aux dix ou vingt prochaines années, on se permet de se désengager des changements sociaux qui peuvent accompagner de telles avancées technologiques. Réfléchir à ce problème nous permet aussi pour éviter de penser à des types plus extrêmes d’intelligence artificielle, dans lesquels nous modélisons Alephzero comme un outil puissant plutôt que comme un collaborateur vivant.
Nous pouvons nous réconforter ainsi : en fait, cette prémisse est trop loin de nous, et nous n’avons pas besoin d’y penser. Mais si nous laissons la moindre chance, cela pourrait arriver dans vingt ans.
Fournit un modèle très approximatif illustrant une partie de notre mécanisme de valeur à travers les interactions bayésiennes entre mathématiciens et réseaux de problèmes. Nous examinons maintenant comment « Alephzero » aura un impact sur ce réseau et en changera le résultat.
Comme nous pouvons le constater, la difficulté perçue est un élément important de la façon dont nous créons de la valeur.
Peu importe la situation spécifique, "Alephzero" changera notre capacité à résoudre des problèmes, changeant ainsi notre perception de la difficulté du problème.
Les parties du processus mathématique qui peuvent être accélérées le plus rapidement verront la plus grande réduction de leur difficulté perçue, et selon notre modèle ci-dessus, l'État subira la plus grande réduction. Un schéma similaire se produit dans de nombreux cas d’automatisation.
Enfin, "Alephzero" élargira considérablement toute la gamme des problèmes intéressants en mathématiques. Cela uniformiserait les règles du jeu entre les mathématiciens professionnels et tout le monde.
Comment les machines peuvent rendre les mathématiques plus agrégées

Adresse papier : https://www.ams.org/journals/bull/2024-61-02/S0273-0979-2024-01827-8 / S0273-0979-2024-01827-8.pdf

Le mathématicien Zheng Lejun estime que puisque la technologie a changé la façon dont nous étudions les mathématiques, nous pouvons utiliser cette technologie pour rendre les mathématiques plus « agrégées », et c'est il ne s’agit pas de rendre les mathématiciens humains superflus face aux progrès technologiques.
En réfléchissant à ce que signifie « faire des mathématiques », elle a examiné les aspects suivants de la technologie mathématique : l'enseignement et l'apprentissage, la pose de questions, la collaboration, la communication et l'acte de faire de la recherche.
Il ne s'agit pas d'une analyse rigoureuse, mais d'une sage réflexion basée sur son expérience de mathématicienne.
Lejun Zheng estime que bien qu'il existe des vérificateurs d'épreuves assistés par ordinateur et même des générateurs de preuves, la technologie n'a pas encore véritablement empiété sur les aspects les plus profonds, créatifs et humains de la recherche mathématique.
La partie créative profonde consiste d'abord à trouver des idées - des idées de définitions, des idées de preuves, des idées pour établir des liens entre différentes parties des mathématiques, des idées pour de nouvelles façons d'exprimer les choses, des idées de symboles et de terminologie, des idées de raisonnement graphique. ainsi que des idées de représentation visuelle.
Pour que les machines effectuent des recherches mathématiques, nous devons trouver un moyen de leur dire de le faire. Il est difficile de leur dire comment le faire si nous ne savons pas comment le faire nous-mêmes.
Les machines peuvent effectuer un certain niveau de vérification des preuves, mais secrètement, les mathématiciens savent que nous ne pouvons pas écrire des preuves complètement rigoureuses - nous élaborons des arguments basés sur la logique et suivons des étapes logiques que nous pensons que nos pairs seront capable de remplir. support.
Nous ne définissons pas la taille de ces étapes, il est donc difficile de dire à la machine de le faire.
Générer des preuves est une compétence complètement différente de simplement les vérifier, comme le sait tout étudiant en mathématiques. Il est beaucoup plus facile de suivre le témoignage de quelqu'un d'autre que d'en inventer un nouveau soi-même. Cela ne veut pas dire que les ordinateurs ne pourront jamais surpasser les mathématiciens humains en termes de capacités de recherche mathématique.
À son avis, ce qui rend les ordinateurs plus puissants que les mathématiciens humains, c'est que-
Ils ont une plus grande capacité à rechercher toutes les actions possibles en recherchant tous les résultats logiques possibles actuellement connus, ils peuvent essayer de proposer de nouvelles mathématiques. .
Cela nécessite un acte d'imagination, de conjectures et d'intuition, qu'est-ce qui suffirait à un ordinateur pour faire cela ? L'idée est très intéressante.
Les ordinateurs peuvent-ils nous aider à faire un raisonnement logique

Adresse papier : https://www.ams.org/journals/bull/2024-61-02/S0273-0979-2024-01833-3/S0273-0979-2024-01833-3.pdf

Les ordinateurs ont révolutionné la façon dont nous menons des recherches mathématiques, rendant les calculs complexes un jeu d'enfant.
Mais ensuite, deviendront-ils des assistants de notre raisonnement logique ? Pourraient-ils un jour raisonner de manière indépendante ?
Cet article vous donnera un aperçu des récents progrès importants dans les réseaux de neurones, les démonstrateurs de théorèmes informatiques et les grands modèles de langage.
Comment les outils formels peuvent nous aider à faire de meilleures recherches mathématiques
Adresse papier : https://www.ams.org/journals/bull/2024-61-02/S0273- 0979- 2024-01832-1/S0273-0979-2024-01832-1.pdf

Depuis le début du 20e siècle, nous avons compris que des définitions et des preuves mathématiques peuvent être obtenues grâce à des systèmes formels avec une syntaxe et une syntaxe strictes. les règles sont représentées.
Sur cette base, le développement d'assistants de preuve informatiques permet d'encoder des connaissances mathématiques sous forme numérique.
Cet article explorera comment ce type de technologie et ses outils associés peuvent nous aider à mener de meilleures recherches mathématiques.
Utilisez le prouveur de théorème pour simplifier des problèmes complexes dans la recherche mathématique

Adresse papier : https://www.ams.org/journals/bull/2024-61-02/ S0273- 0979-2024-01831-X/S0273-0979-2024-01831-X.pdf
Cet article explore comment un prouveur de théorème interactif peut être utilisé pour simplifier des problèmes complexes dans la recherche mathématique en fixant des limites abstraites.
Nouvel univers étrange : LLM permet aux mathématiciens de communiquer avec des assistants de preuve dans un langage plus naturel

Adresse papier : https://www.ams.org/journals/bull/2024-61 - Les programmes informatiques actuels, également appelés assistants de preuve, sont capables de vérifier l'exactitude des preuves mathématiques, Mais le langage de preuve spécialisé qu’ils utilisent constitue un obstacle pour de nombreux mathématiciens.
 Les grands modèles de langage (LLM) ont le potentiel de briser cette barrière, permettant aux mathématiciens de communiquer avec les assistants de preuve dans un langage plus naturel. Non seulement cela développe leur intuition, mais cela garantit également que leur raisonnement est correct.
Les grands modèles de langage (LLM) ont le potentiel de briser cette barrière, permettant aux mathématiciens de communiquer avec les assistants de preuve dans un langage plus naturel. Non seulement cela développe leur intuition, mais cela garantit également que leur raisonnement est correct.
Utilisez des outils d'apprentissage profond pour effectuer des recherches mathématiques pures
Adresse papier : https://www.ams.org/journals/bull/2024-61-02/S0273-0979-2024 - 01829-1/S0273-0979-2024-01829-1.pdf

Cet article porte sur l'expérience personnelle et le partage informel de ce à quoi un mathématicien pur peut s'attendre lorsqu'il essaie d'utiliser des outils d'apprentissage profond dans la recherche.


Adresse papier : https://www.ams.org/journals/bull/2024-61-02/S0273-0979-2024-01828-X/S0273-0979-2024-01828-X.pdf

Cet article explore les capacités et les limites de la technologie actuelle de l'IA dans la résolution de problèmes de mots qui combinent mathématiques de base et raisonnement de bon sens.
L'auteur passe en revue trois méthodes développées à l'aide de la technologie du langage naturel de l'IA : donner directement des réponses, générer des programmes informatiques qui résolvent des problèmes et générer des représentations formelles pouvant être utilisées par des testeurs automatisés de théorèmes.
L'auteur estime que l'importance de ces limitations dans le développement de la technologie de l'IA pour la recherche mathématique pure n'a pas encore été clairement définie, mais elles sont extrêmement critiques dans les applications mathématiques et sont également importantes dans le développement de programmes capables de comprendre le contenu mathématique. écrit par des humains.
Qu'est-ce que la preuve à l'ère de la machine
Adresse papier : https://www.ams.org/journals/bull/2024-61-02/S0273-0979-2024-01826- 6 /S0273-0979-2024-01826-6.pdf

Dans cet article, l'auteur explore la nature des preuves et leur évolution à l'ère de la machine en comparant les valeurs de la vérification traditionnelle et de l'analyse de la vérification informatique.
La méthode finalement proposée dans l'article pourrait permettre aux ordinateurs de prouver des stratégies réussies empruntées à l'expérience humaine.
L'automatisation permet aux mathématiciens de réfléchir sur leur propre valeur
Adresse papier : https://www.ams.org/journals/bull/2024-61-02/S0273-0979-2024-01825 -4/S0273-0979-2024-01825-4.pdf

Dans cet article, l'auteur critique sévèrement le manque de réflexion de ses collègues, notamment lorsqu'il s'agit de débats importants sur l'avenir mécanisé des mathématiques. l'intelligence artificielle à un niveau plus large dans la société.
Fractions continues dans les champs de nombres p-adiques

Adresse papier : https://www.ams.org/journals/bull/2024-61-02/S0273-0979-2024-01819 - 9/S0273-0979-2024-01819-9.pdf
Les fractions continues ont une longue histoire en théorie des nombres, en particulier dans le domaine de l'approximation diophantienne.
Cet article vise à décrire les principaux résultats de la théorie des fractions continues p-adiques, qui est une fraction continue définie sur le champ numérique p-adique Qp.
Le contenu partira des concepts de base pour présenter les derniers progrès et les problèmes ouverts actuellement rencontrés.
Tao Zhexuan a posté : Preuve assistée par machine
Au fait, Tao Zhexuan a également utilisé la « Preuve assistée par machine » de l'article qu'il a écrit auparavant.

Adresse papier : https://terrytao.files.wordpress.com/2024/03/machine-assisted-proof-notices.pdf

Dans cet article, Tao Zhexuan a déclaré qu'avec l'aide de la capacité du LLM à traiter la saisie en langage naturel, ils sont susceptibles de devenir une plate-forme conviviale, permettant aux mathématiciens sans connaissances spécifiques en logiciels d'utiliser des outils avancés.
Maintenant, lui et de nombreux scientifiques sont habitués à utiliser ces modèles pour générer des codes simples dans divers langages, y compris des packages d'algèbre symbolique, ou pour créer des diagrammes et des images complexes.
Actuellement, en raison de la forte dépendance aux efforts humains pour la vérification formelle des preuves, il devient peu pratique de formaliser entièrement un grand nombre d'articles de recherche en cours en temps réel.
Dans le domaine des équations aux dérivées partielles, il est souvent nécessaire d'estimer des expressions intégrales impliquant une ou plusieurs fonctions inconnues (comme la solution d'une EDP) à travers plusieurs pages de calculs.
Cela implique d'utiliser les limites de ces fonctions dans différentes normes d'espace de fonctions (telles que la norme d'espace de Sobolev), combinées avec des inégalités standards (telles que l'inégalité de Hölder et l'inégalité de Sobolev), et telles que l'intégrale par parties ou le signe intégral. Équations différentielles .
Bien que ce type de calcul soit une opération de routine, il peut contenir divers degrés d'erreurs (comme des erreurs de signe). Il est fastidieux et long pour les réviseurs de vérifier ces calculs en détail, et ces calculs eux-mêmes sont en cours. ajout à la finale Au-delà du fait que l'estimation est correcte, il est difficile de fournir une compréhension ou un aperçu mathématique plus approfondi.
Il est concevable qu'à l'avenir, des outils soient développés pour établir des estimations mathématiques de manière automatique ou semi-automatique, et remplacer les preuves d'estimation longues et peu inspirantes actuelles par un lien vers un certificat de preuve formel.
En allant plus loin, nous pourrions peut-être nous attendre à ce que, sur la base d'un premier ensemble d'hypothèses et de méthodes, un futur outil d'IA soit capable de proposer la meilleure estimation possible, sans avoir à faire au préalable du papier. des calculs au crayon pour prédire ce que pourrait être cette estimation.
À l'heure actuelle, l'espace d'états possibles estimé est trop complexe pour être exploré automatiquement ; mais avec le développement de la technologie, la possibilité de réaliser une telle exploration automatisée n'est pas hors de portée.
Une fois mis en œuvre, nous serons en mesure de mener une exploration mathématique à une échelle qui semble actuellement irréalisable.
Prenons comme exemple les équations aux dérivées partielles. Les recherches actuelles n’étudient généralement qu’une ou deux équations à la fois, mais à l’avenir, nous pourrons peut-être étudier des centaines d’équations en même temps ;
Par exemple, développez d'abord un argument complet pour une équation, puis laissez l'outil d'IA adapter ces arguments à un grand nombre de familles d'équations connexes. Si nécessaire, lorsque l'expansion de l'argument rencontre des situations non conventionnelles, l'IA posera des questions à l'auteur.
Maintenant, dans d'autres domaines des mathématiques, comme la théorie des graphes, les premiers signes de cette exploration mathématique à grande échelle commencent déjà à apparaître.
Cependant, ces tentatives préliminaires actuelles sont difficiles à promouvoir à grande échelle car elles s'appuient sur des modèles d'IA extrêmement intensifs en termes de calcul ou nécessitent une grande participation et une supervision humaine de niveau expert.
Cependant, Terence Tao estime que dans un avenir proche, nous assisterons à la naissance de méthodes mathématiques assistées par machine plus innovantes.
Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!

Outils d'IA chauds

Undresser.AI Undress
Application basée sur l'IA pour créer des photos de nu réalistes

AI Clothes Remover
Outil d'IA en ligne pour supprimer les vêtements des photos.

Undress AI Tool
Images de déshabillage gratuites

Clothoff.io
Dissolvant de vêtements AI

AI Hentai Generator
Générez AI Hentai gratuitement.

Article chaud

Outils chauds

Bloc-notes++7.3.1
Éditeur de code facile à utiliser et gratuit

SublimeText3 version chinoise
Version chinoise, très simple à utiliser

Envoyer Studio 13.0.1
Puissant environnement de développement intégré PHP

Dreamweaver CS6
Outils de développement Web visuel

SublimeText3 version Mac
Logiciel d'édition de code au niveau de Dieu (SublimeText3)
 Le modèle MoE open source le plus puissant au monde est ici, avec des capacités chinoises comparables à celles du GPT-4, et le prix ne représente que près d'un pour cent de celui du GPT-4-Turbo.
May 07, 2024 pm 04:13 PM
Le modèle MoE open source le plus puissant au monde est ici, avec des capacités chinoises comparables à celles du GPT-4, et le prix ne représente que près d'un pour cent de celui du GPT-4-Turbo.
May 07, 2024 pm 04:13 PM
Imaginez un modèle d'intelligence artificielle qui non seulement a la capacité de surpasser l'informatique traditionnelle, mais qui permet également d'obtenir des performances plus efficaces à moindre coût. Ce n'est pas de la science-fiction, DeepSeek-V2[1], le modèle MoE open source le plus puissant au monde est ici. DeepSeek-V2 est un puissant mélange de modèle de langage d'experts (MoE) présentant les caractéristiques d'une formation économique et d'une inférence efficace. Il est constitué de 236B paramètres, dont 21B servent à activer chaque marqueur. Par rapport à DeepSeek67B, DeepSeek-V2 offre des performances plus élevées, tout en économisant 42,5 % des coûts de formation, en réduisant le cache KV de 93,3 % et en augmentant le débit de génération maximal à 5,76 fois. DeepSeek est une entreprise explorant l'intelligence artificielle générale
 KAN, qui remplace MLP, a été étendu à la convolution par des projets open source
Jun 01, 2024 pm 10:03 PM
KAN, qui remplace MLP, a été étendu à la convolution par des projets open source
Jun 01, 2024 pm 10:03 PM
Plus tôt ce mois-ci, des chercheurs du MIT et d'autres institutions ont proposé une alternative très prometteuse au MLP – KAN. KAN surpasse MLP en termes de précision et d’interprétabilité. Et il peut surpasser le MLP fonctionnant avec un plus grand nombre de paramètres avec un très petit nombre de paramètres. Par exemple, les auteurs ont déclaré avoir utilisé KAN pour reproduire les résultats de DeepMind avec un réseau plus petit et un degré d'automatisation plus élevé. Plus précisément, le MLP de DeepMind compte environ 300 000 paramètres, tandis que le KAN n'en compte qu'environ 200. KAN a une base mathématique solide comme MLP est basé sur le théorème d'approximation universelle, tandis que KAN est basé sur le théorème de représentation de Kolmogorov-Arnold. Comme le montre la figure ci-dessous, KAN a
 Bonjour, Atlas électrique ! Le robot Boston Dynamics revient à la vie, des mouvements étranges à 180 degrés effraient Musk
Apr 18, 2024 pm 07:58 PM
Bonjour, Atlas électrique ! Le robot Boston Dynamics revient à la vie, des mouvements étranges à 180 degrés effraient Musk
Apr 18, 2024 pm 07:58 PM
Boston Dynamics Atlas entre officiellement dans l’ère des robots électriques ! Hier, l'Atlas hydraulique s'est retiré "en larmes" de la scène de l'histoire. Aujourd'hui, Boston Dynamics a annoncé que l'Atlas électrique était au travail. Il semble que dans le domaine des robots humanoïdes commerciaux, Boston Dynamics soit déterminé à concurrencer Tesla. Après la sortie de la nouvelle vidéo, elle a déjà été visionnée par plus d’un million de personnes en seulement dix heures. Les personnes âgées partent et de nouveaux rôles apparaissent. C'est une nécessité historique. Il ne fait aucun doute que cette année est l’année explosive des robots humanoïdes. Les internautes ont commenté : Les progrès des robots ont fait ressembler la cérémonie d'ouverture de cette année à des êtres humains, et le degré de liberté est bien plus grand que celui des humains. Mais n'est-ce vraiment pas un film d'horreur ? Au début de la vidéo, Atlas est allongé calmement sur le sol, apparemment sur le dos. Ce qui suit est à couper le souffle
 L'IA bouleverse la recherche mathématique ! Le lauréat de la médaille Fields et mathématicien sino-américain a dirigé 11 articles les mieux classés | Aimé par Terence Tao
Apr 09, 2024 am 11:52 AM
L'IA bouleverse la recherche mathématique ! Le lauréat de la médaille Fields et mathématicien sino-américain a dirigé 11 articles les mieux classés | Aimé par Terence Tao
Apr 09, 2024 am 11:52 AM
L’IA change effectivement les mathématiques. Récemment, Tao Zhexuan, qui a prêté une attention particulière à cette question, a transmis le dernier numéro du « Bulletin de l'American Mathematical Society » (Bulletin de l'American Mathematical Society). En se concentrant sur le thème « Les machines changeront-elles les mathématiques ? », de nombreux mathématiciens ont exprimé leurs opinions. L'ensemble du processus a été plein d'étincelles, intense et passionnant. L'auteur dispose d'une équipe solide, comprenant Akshay Venkatesh, lauréat de la médaille Fields, le mathématicien chinois Zheng Lejun, l'informaticien de l'Université de New York Ernest Davis et de nombreux autres universitaires bien connus du secteur. Le monde de l’IA a radicalement changé. Vous savez, bon nombre de ces articles ont été soumis il y a un an.
 Google est ravi : les performances de JAX surpassent Pytorch et TensorFlow ! Cela pourrait devenir le choix le plus rapide pour la formation à l'inférence GPU
Apr 01, 2024 pm 07:46 PM
Google est ravi : les performances de JAX surpassent Pytorch et TensorFlow ! Cela pourrait devenir le choix le plus rapide pour la formation à l'inférence GPU
Apr 01, 2024 pm 07:46 PM
Les performances de JAX, promu par Google, ont dépassé celles de Pytorch et TensorFlow lors de récents tests de référence, se classant au premier rang sur 7 indicateurs. Et le test n’a pas été fait sur le TPU présentant les meilleures performances JAX. Bien que parmi les développeurs, Pytorch soit toujours plus populaire que Tensorflow. Mais à l’avenir, des modèles plus volumineux seront peut-être formés et exécutés sur la base de la plate-forme JAX. Modèles Récemment, l'équipe Keras a comparé trois backends (TensorFlow, JAX, PyTorch) avec l'implémentation native de PyTorch et Keras2 avec TensorFlow. Premièrement, ils sélectionnent un ensemble de
 Les robots Tesla travaillent dans les usines, Musk : Le degré de liberté des mains atteindra 22 cette année !
May 06, 2024 pm 04:13 PM
Les robots Tesla travaillent dans les usines, Musk : Le degré de liberté des mains atteindra 22 cette année !
May 06, 2024 pm 04:13 PM
La dernière vidéo du robot Optimus de Tesla est sortie, et il peut déjà fonctionner en usine. À vitesse normale, il trie les batteries (les batteries 4680 de Tesla) comme ceci : Le responsable a également publié à quoi cela ressemble à une vitesse 20 fois supérieure - sur un petit "poste de travail", en sélectionnant et en sélectionnant et en sélectionnant : Cette fois, il est publié L'un des points forts de la vidéo est qu'Optimus réalise ce travail en usine, de manière totalement autonome, sans intervention humaine tout au long du processus. Et du point de vue d'Optimus, il peut également récupérer et placer la batterie tordue, en se concentrant sur la correction automatique des erreurs : concernant la main d'Optimus, le scientifique de NVIDIA Jim Fan a donné une évaluation élevée : la main d'Optimus est l'un des robots à cinq doigts du monde. le plus adroit. Ses mains ne sont pas seulement tactiles
 DualBEV : dépassant largement BEVFormer et BEVDet4D, ouvrez le livre !
Mar 21, 2024 pm 05:21 PM
DualBEV : dépassant largement BEVFormer et BEVDet4D, ouvrez le livre !
Mar 21, 2024 pm 05:21 PM
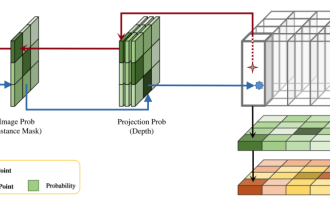
Cet article explore le problème de la détection précise d'objets sous différents angles de vue (tels que la perspective et la vue à vol d'oiseau) dans la conduite autonome, en particulier comment transformer efficacement les caractéristiques de l'espace en perspective (PV) en vue à vol d'oiseau (BEV). implémenté via le module Visual Transformation (VT). Les méthodes existantes sont globalement divisées en deux stratégies : la conversion 2D en 3D et la conversion 3D en 2D. Les méthodes 2D vers 3D améliorent les caractéristiques 2D denses en prédisant les probabilités de profondeur, mais l'incertitude inhérente aux prévisions de profondeur, en particulier dans les régions éloignées, peut introduire des inexactitudes. Alors que les méthodes 3D vers 2D utilisent généralement des requêtes 3D pour échantillonner des fonctionnalités 2D et apprendre les poids d'attention de la correspondance entre les fonctionnalités 3D et 2D via un transformateur, ce qui augmente le temps de calcul et de déploiement.
 FisheyeDetNet : le premier algorithme de détection de cible basé sur une caméra fisheye
Apr 26, 2024 am 11:37 AM
FisheyeDetNet : le premier algorithme de détection de cible basé sur une caméra fisheye
Apr 26, 2024 am 11:37 AM
La détection de cibles est un problème relativement mature dans les systèmes de conduite autonome, parmi lesquels la détection des piétons est l'un des premiers algorithmes à être déployés. Des recherches très complètes ont été menées dans la plupart des articles. Cependant, la perception de la distance à l’aide de caméras fisheye pour une vue panoramique est relativement moins étudiée. En raison de la distorsion radiale importante, la représentation standard du cadre de délimitation est difficile à mettre en œuvre dans les caméras fisheye. Pour alléger la description ci-dessus, nous explorons les conceptions étendues de boîtes englobantes, d'ellipses et de polygones généraux dans des représentations polaires/angulaires et définissons une métrique de segmentation d'instance mIOU pour analyser ces représentations. Le modèle fisheyeDetNet proposé avec une forme polygonale surpasse les autres modèles et atteint simultanément 49,5 % de mAP sur l'ensemble de données de la caméra fisheye Valeo pour la conduite autonome.





