En termes simples, un modèle d'apprentissage automatique est une fonction mathématique qui mappe les données d'entrée à une sortie prédite. Plus précisément, un modèle d'apprentissage automatique est une fonction mathématique qui ajuste les paramètres du modèle en apprenant à partir des données d'entraînement afin de minimiser l'erreur entre la sortie prédite et la véritable étiquette.
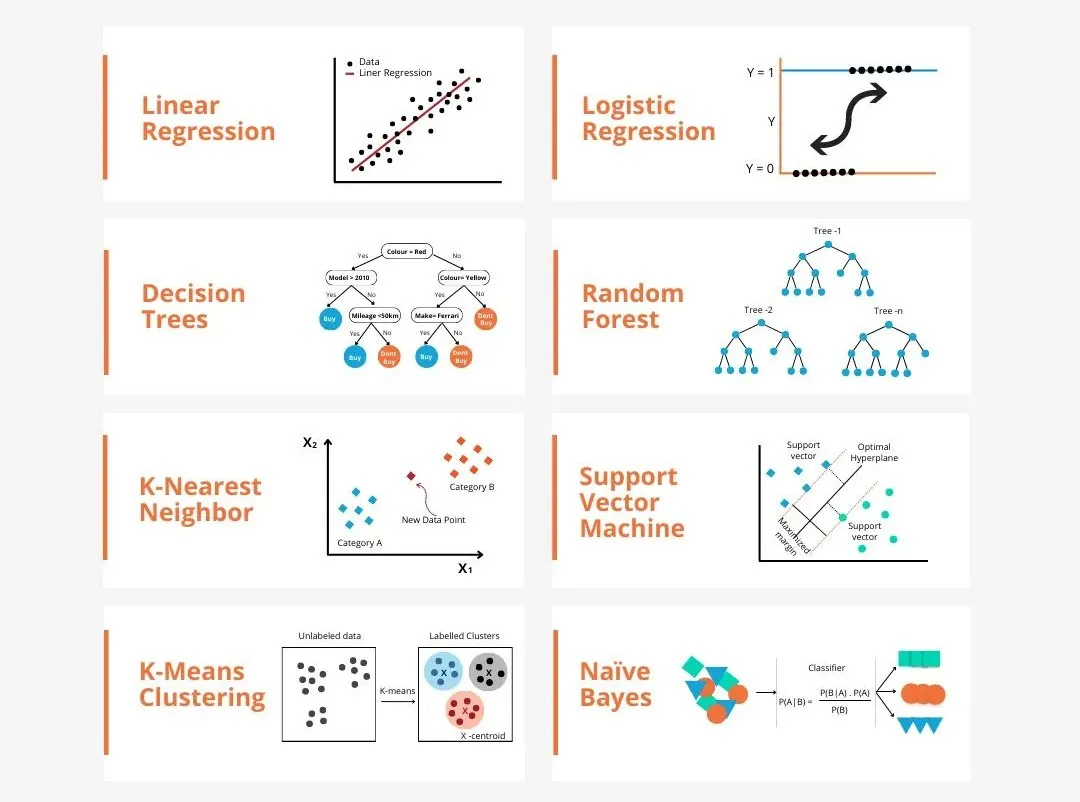
Il existe de nombreux modèles dans l'apprentissage automatique, tels que le modèle de régression logistique, le modèle d'arbre de décision, le modèle de machine à vecteurs de support, etc. Chaque modèle a son type de données applicable et son type de problème. Dans le même temps, il existe de nombreux points communs entre les différents modèles, ou il existe une voie cachée pour l’évolution du modèle.
Prenons l'exemple du perceptron connexionniste. En augmentant le nombre de couches cachées du perceptron, nous pouvons le transformer en un réseau neuronal profond. Si une fonction noyau est ajoutée au perceptron, elle peut être convertie en SVM. Ce processus peut démontrer intuitivement les connexions intrinsèques entre les différents modèles, ainsi que les transformations possibles entre les modèles. En fonction des similitudes, j'ai divisé grossièrement (pas rigoureusement) les modèles dans les 6 catégories suivantes pour faciliter la découverte des points communs fondamentaux et les analyser en profondeur un par un !
Le modèle connexionniste est un modèle informatique qui simule la structure et le fonctionnement du réseau neuronal du cerveau humain. Son unité de base est un neurone. Chaque neurone reçoit des informations d'autres neurones et modifie l'influence de ces informations sur le neurone en ajustant les poids. Le réseau neuronal est une boîte noire. Grâce à l'action de plusieurs couches cachées non linéaires, il peut obtenir un effet proche.
Les modèles représentatifs incluent DNN, SVM, Transformer et LSTM. Dans certains cas, la dernière couche d'un réseau neuronal profond peut être considérée comme un modèle de régression logistique, utilisé pour classer les données d'entrée. La machine à vecteurs de support peut également être considérée comme un type spécial de réseau neuronal. Elle ne comporte que deux couches : la couche d'entrée et la couche de sortie implémentent en outre une transformation non linéaire complexe via les fonctions du noyau pour obtenir des effets similaires à ceux des réseaux neuronaux profonds. Ce qui suit est une analyse du principe du modèle DNN classique :
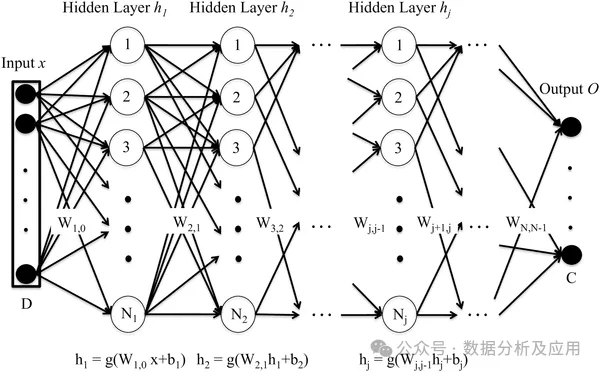
Le réseau neuronal profond (DNN) est composé de plusieurs couches de neurones Grâce au processus de propagation vers l'avant, les données d'entrée sont transférées à chaque couche de neurones. , et calculé couche par couche pour obtenir la sortie. Chaque couche de neurones reçoit la sortie des neurones de la couche précédente en entrée et la transmet aux neurones de la couche suivante. Le processus de formation du DNN est mis en œuvre via l'algorithme de rétro-propagation. Pendant le processus de formation, l'erreur entre la couche de sortie et l'étiquette réelle est calculée, et l'erreur est rétropropagée à chaque couche de neurones, et les poids et termes de biais des neurones sont mis à jour selon l'algorithme de descente de gradient. En répétant ce processus à plusieurs reprises, les paramètres du réseau sont continuellement optimisés et l'erreur de prédiction du réseau est finalement minimisée.
L'avantage du réseau neuronal profond (DNN) est sa puissante capacité d'apprentissage des fonctionnalités. DNN peut apprendre automatiquement les caractéristiques des données sans concevoir manuellement de fonctionnalités. Capacité de généralisation hautement non linéaire et forte. L’inconvénient est que DNN nécessite un grand nombre de paramètres, ce qui peut entraîner des problèmes de surajustement. Dans le même temps, DNN nécessite une grande quantité de calculs et prend beaucoup de temps à s'entraîner. Ce qui suit est un exemple simple de code Python, utilisant la bibliothèque Keras pour créer un modèle de réseau neuronal profond :
from keras.models import Sequentialfrom keras.layers import Densefrom keras.optimizers import Adamfrom keras.losses import BinaryCrossentropyimport numpy as np# 构建模型model = Sequential()model.add(Dense(64, activatinotallow='relu', input_shape=(10,))) # 输入层有10个特征model.add(Dense(64, activatinotallow='relu')) # 隐藏层有64个神经元model.add(Dense(1, activatinotallow='sigmoid')) # 输出层有1个神经元，使用sigmoid激活函数进行二分类任务# 编译模型model.compile(optimizer=Adam(lr=0.001), loss=BinaryCrossentropy(), metrics=['accuracy'])# 生成模拟数据集x_train = np.random.rand(1000, 10) # 1000个样本，每个样本有10个特征y_train = np.random.randint(2, size=1000) # 1000个标签，二分类任务# 训练模型model.fit(x_train, y_train, epochs=10, batch_size=32) # 训练10个轮次，每次使用32个样本进行训练
Le modèle de symbolisme est une méthode de simulation intelligente basée sur un raisonnement logique, qui estime que les êtres humains sont un système de symboles physiques, et les ordinateurs sont également des systèmes de symboles physiques. Par conséquent, la base de règles et le moteur de raisonnement de l'ordinateur peuvent être utilisés pour simuler le comportement intelligent humain, c'est-à-dire que les opérations symboliques de l'ordinateur sont utilisées pour simuler les processus cognitifs humains (. Pour parler franchement, cela signifie stocker la logique humaine dans l’ordinateur pour réaliser une exécution intelligente).
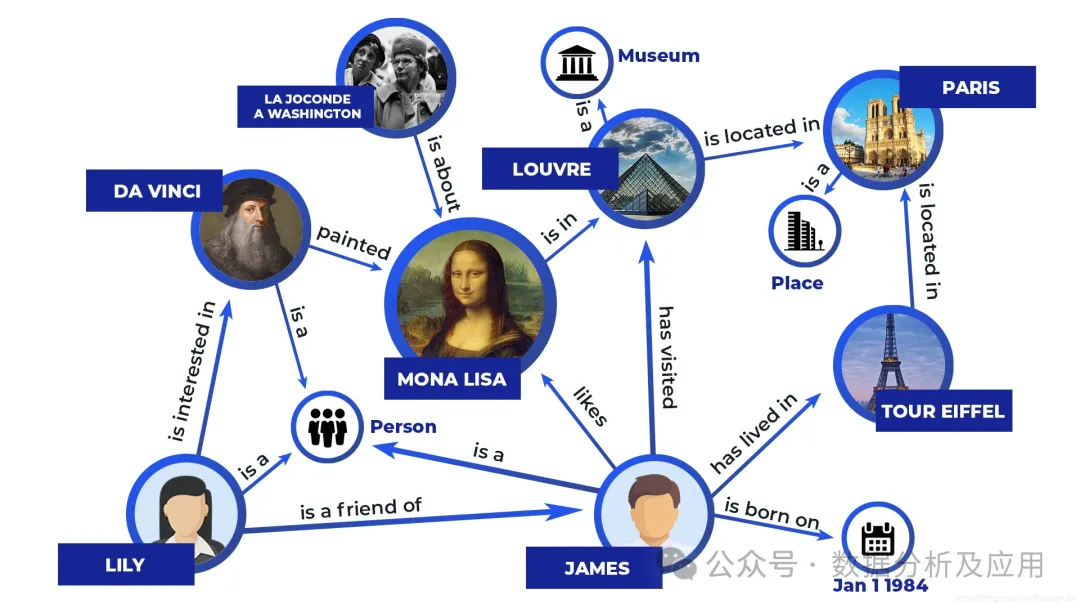
Les modèles représentatifs comprennent des systèmes experts, des bases de connaissances et des graphiques de connaissances. Le principe est de coder les informations dans un ensemble de symboles identifiables et d'exploiter les symboles via des règles explicites pour produire des résultats d'opération. Un exemple simple de système expert est le suivant :
# 定义规则库rules = [{"name": "rule1", "condition": "sym1 == 'A' and sym2 == 'B'", "action": "result = 'C'"},{"name": "rule2", "condition": "sym1 == 'B' and sym2 == 'C'", "action": "result = 'D'"},{"name": "rule3", "condition": "sym1 == 'A' or sym2 == 'B'", "action": "result = 'E'"},]# 定义推理引擎def infer(rules, sym1, sym2):for rule in rules:if rule["condition"] == True:# 条件为真时执行动作return rule["action"]return None# 没有满足条件的规则时返回None# 测试专家系统print(infer(rules, 'A', 'B'))# 输出: Cprint(infer(rules, 'B', 'C'))# 输出: Dprint(infer(rules, 'A', 'C'))# 输出: Eprint(infer(rules, 'B', 'B'))# 输出: E决策树模型是一种非参数的分类和回归方法，它利用树形图表示决策过程。更通俗来讲，树模型的数学描述就是“分段函数”。它利用信息论中的熵理论选择决策树的最佳划分属性，以构建出一棵具有最佳分类性能的决策树。
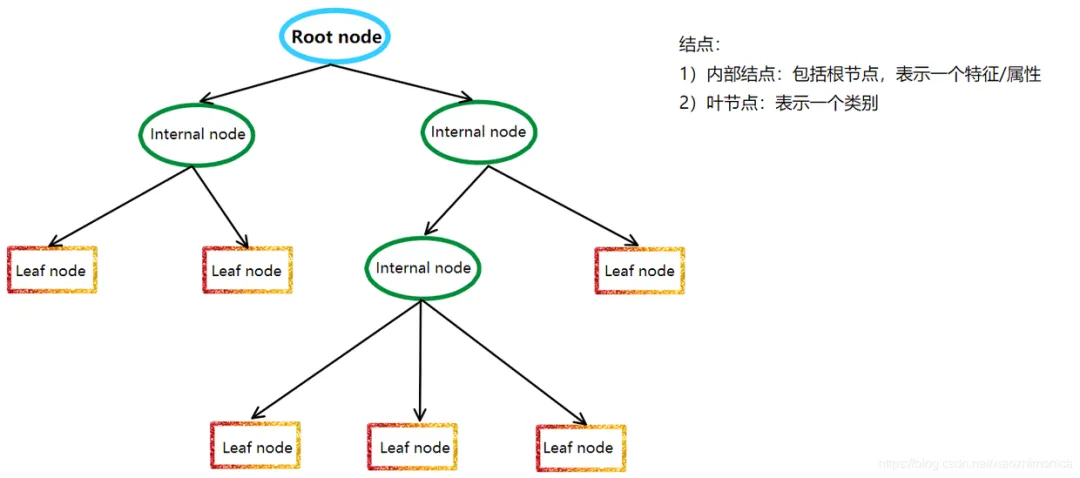
决策树模型的基本原理是递归地将数据集划分成若干个子数据集，直到每个子数据集都属于同一类别或者满足某个停止条件。在划分过程中，决策树模型采用信息增益、信息增益率、基尼指数等指标来评估划分的好坏，以选择最佳的划分属性。
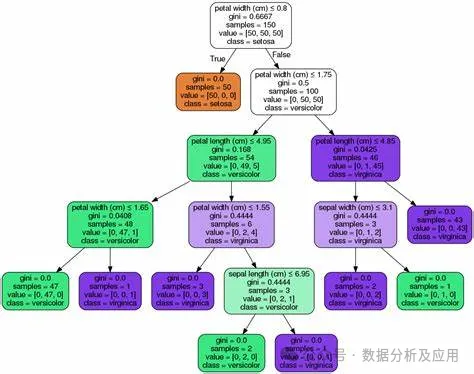
决策树模型的代表模型有很多，其中最著名的有ID3、C4.5、CART等。ID3算法是决策树算法的鼻祖，它采用信息增益来选择最佳划分属性；C4.5算法是ID3算法的改进版，它采用信息增益率来选择最佳划分属性，同时采用剪枝策略来提高决策树的泛化能力；CART算法则是分类和回归树的简称，它采用基尼指数来选择最佳划分属性，并能够处理连续属性和有序属性。
以下是使用Python中的Scikit-learn库实现CART算法的代码示例：
from sklearn.datasets import load_irisfrom sklearn.model_selection import train_test_splitfrom sklearn.tree import DecisionTreeClassifier, plot_tree# 加载数据集iris = load_iris()X = iris.datay = iris.target# 划分训练集和测试集X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)# 构建决策树模型clf = DecisionTreeClassifier(criterinotallow='gini')clf.fit(X_train, y_train)# 预测测试集结果y_pred = clf.predict(X_test)# 可视化决策树plot_tree(clf)
概率模型是一种基于概率论的数学模型，用于描述随机现象或事件的分布、发生概率以及它们之间的概率关系。概率模型在各个领域都有广泛的应用，如统计学、经济学、机器学习等。
概率模型的原理基于概率论和统计学的基本原理。它使用概率分布来描述随机变量的分布情况，并使用概率规则来描述事件之间的条件关系。通过这些原理，概率模型可以对随机现象或事件进行定量分析和预测。
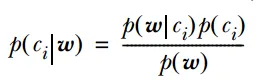
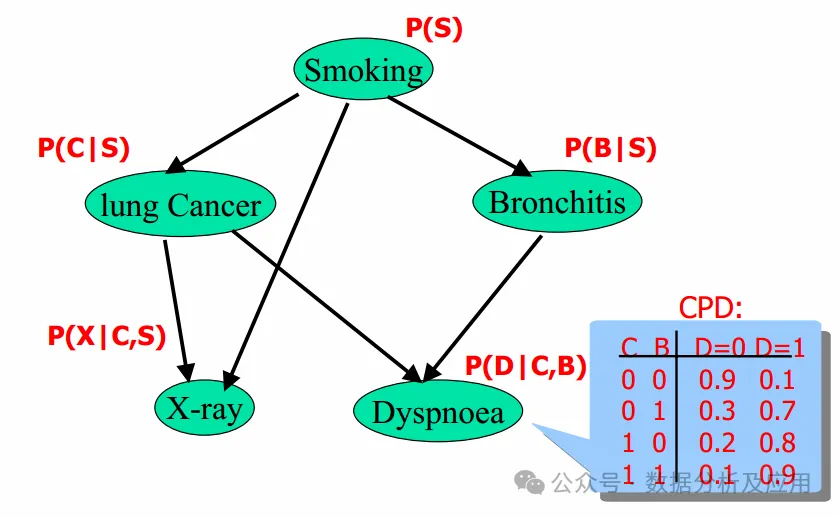
代表模型主要有：朴素贝叶斯分类器、贝叶斯网络、隐马尔可夫模型。其中，朴素贝叶斯分类器和逻辑回归都基于贝叶斯定理，它们都使用概率来表示分类的不确定性。
隐马尔可夫模型和贝叶斯网络都是基于概率的模型，可用于描述随机序列和随机变量之间的关系。
朴素贝叶斯分类器和贝叶斯网络都是基于概率的图模型，可用于描述随机变量之间的概率关系。
以下是使用Python中的Scikit-learn库实现朴素贝叶斯分类器的代码示例：
from sklearn.datasets import load_irisfrom sklearn.model_selection import train_test_splitfrom sklearn.naive_bayes import GaussianNB# 加载数据集iris = load_iris()X = iris.datay = iris.target# 划分训练集和测试集X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)# 构建朴素贝叶斯分类器模型clf = GaussianNB()clf.fit(X_train, y_train)# 预测测试集结果y_pred = clf.predict(X_test)
近邻类模型（本来想命名为距离类模型，但是距离类的定义就比较宽泛了）是一种非参数的分类和回归方法，它基于实例的学习不需要明确的训练和测试集的划分。它通过测量不同数据点之间的距离来决定数据的相似性。
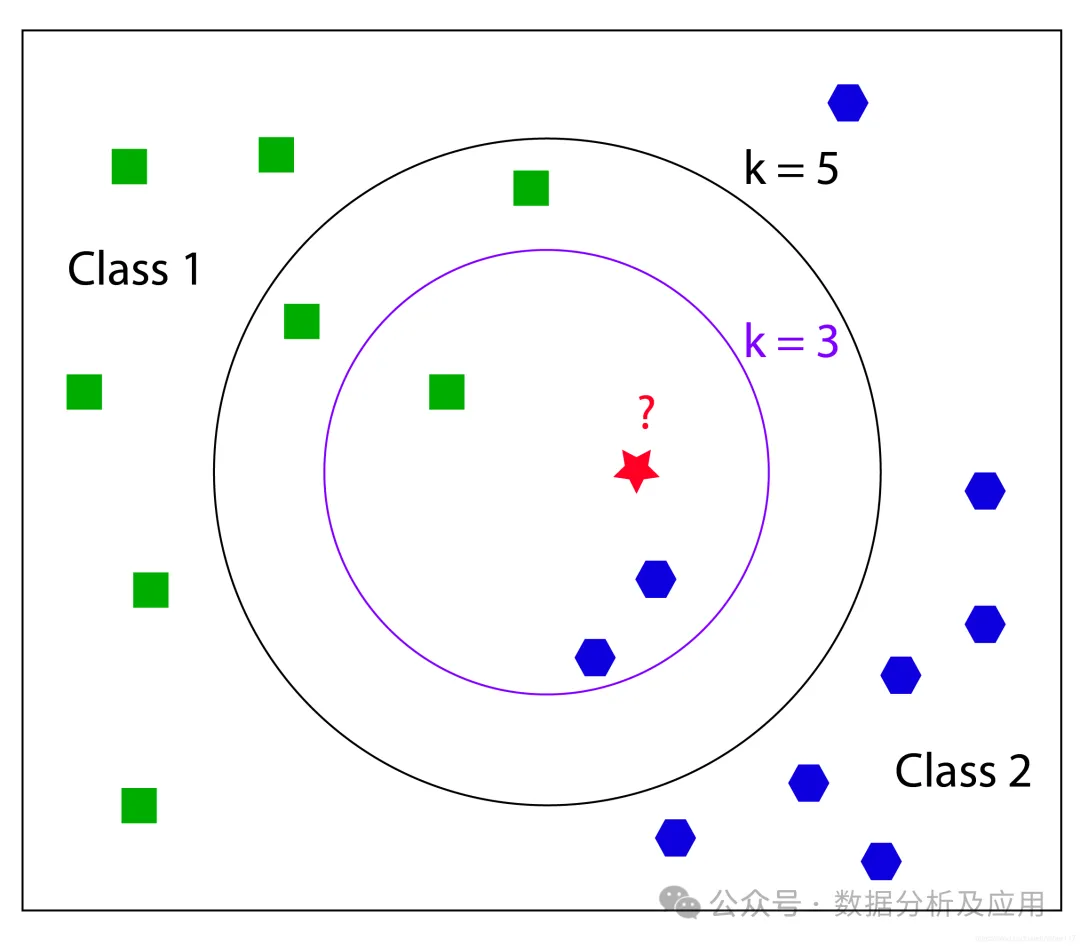
以KNN算法为例，其核心思想是，如果一个样本在特征空间中的 k 个最接近的训练样本中的大多数属于某一个类别，则该样本也属于这个类别。KNN算法基于实例的学习不需要明确的训练和测试集的划分，而是通过测量不同数据点之间的距离来决定数据的相似性。
代表模型有：k-近邻算法（k-Nearest Neighbors，KNN）、半径搜索（Radius Search）、K-means、权重KNN、多级分类KNN（Multi-level Classification KNN）、近似最近邻算法（Approximate Nearest Neighbor， ANN）
近邻模型基于相似的原理，即通过测量不同数据点之间的距离来决定数据的相似性。
除了最基础的KNN算法外，其他变种如权重KNN和多级分类KNN都在基础算法上进行了改进，以更好地适应不同的分类问题。
近似最近邻算法（ANN）是一种通过牺牲精度来换取时间和空间的方式，从大量样本中获取最近邻的方法。ANN算法通过降低存储空间和提高查找效率来处理大规模数据集。它通过“近似”的方法来减少搜索时间，这种方法允许在搜索过程中存在少量误差。
以下是使用Python中的Scikit-learn库实现KNN算法的代码示例：
from sklearn.datasets import load_irisfrom sklearn.model_selection import train_test_splitfrom sklearn.neighbors import KNeighborsClassifier# 加载数据集iris = load_iris()X = iris.datay = iris.target# 划分训练集和测试集X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)# 构建KNN分类器模型knn = KNeighborsClassifier(n_neighbors=3)knn.fit(X_train, y_train)# 预测测试集结果y_pred = knn.predict(X_test)
集成学习（Ensemble Learning）不仅仅是一类的模型，更是一种多模型融合的思想，通过将多个学习器的预测结果进行合并，以提高整体的预测精度和稳定性。在实际应用中，集成学习无疑是数据挖掘的神器！
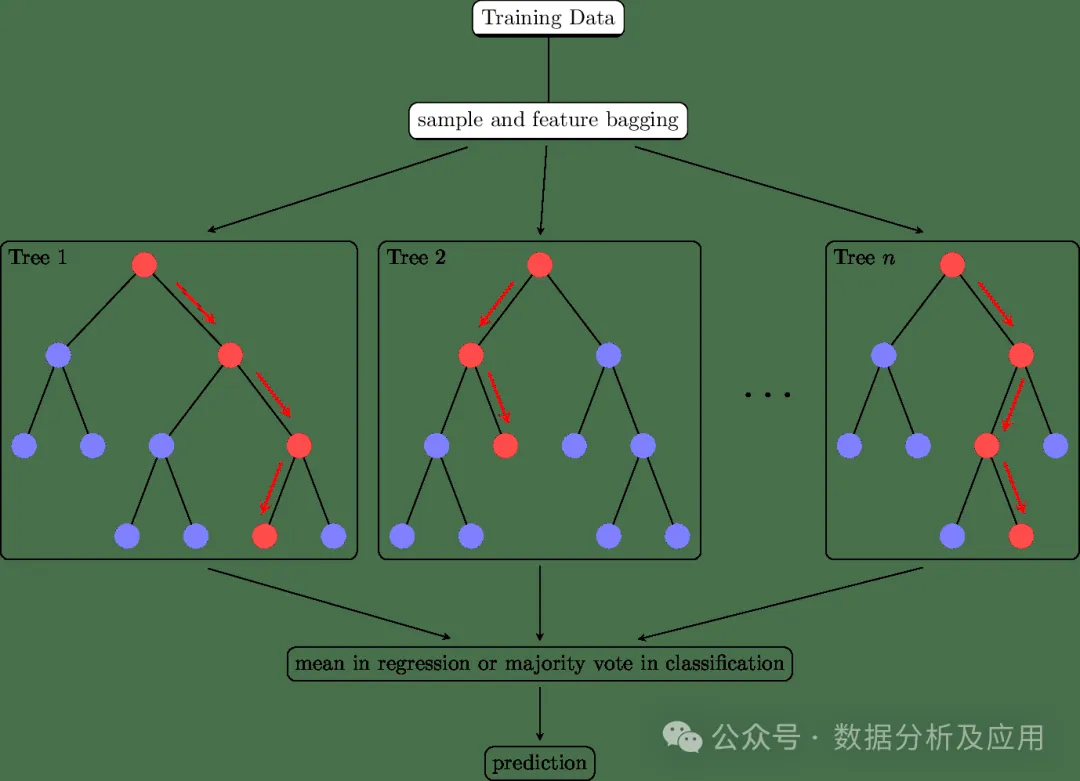
集成学习的核心思想是通过集成多个基学习器来提高整体的预测性能。具体来说，通过将多个学习器的预测结果进行合并，可以减少单一学习器的过拟合和欠拟合问题，提高模型的泛化能力。同时，通过引入多样性（如不同的基学习器、不同的训练数据等），可以进一步提高模型的性能。常用的集成学习方法有：
集成学习代表模型有：随机森林、孤立森林、GBDT、Adaboost、Xgboost等。以下是使用Python中的Scikit-learn库实现随机森林算法的代码示例：
from sklearn.ensemble import RandomForestClassifierfrom sklearn.datasets import load_irisfrom sklearn.model_selection import train_test_split# 加载数据集iris = load_iris()X = iris.datay = iris.target# 划分训练集和测试集X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)# 构建随机森林分类器模型clf = RandomForestClassifier(n_estimators=100, random_state=42)clf.fit(X_train, y_train)# 预测测试集结果y_pred = clf.predict(X_test)
综上，我们通过将相似原理的模型归纳为各种类别，以此逐个类别地探索其原理，可以更为系统全面地了解模型的原理及联系。希望对大家有所帮助！
Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!
![[Web front-end] Démarrage rapide de Node.js](https://img.php.cn/upload/course/000/000/067/662b5d34ba7c0227.png)
