En modifiant la méthode d'initialisation de LoRA, la nouvelle méthode PiSSA de l'Université de Pékin améliore considérablement l'effet de réglage fin

À mesure que le nombre de paramètres des grands modèles augmente de jour en jour, le coût de réglage fin de l'ensemble du modèle devient progressivement inacceptable.

Par conséquent, l'équipe de recherche de l'Université de Pékin a proposé une méthode efficace de réglage fin des paramètres appelée PiSSA, qui dépasse l'effet de réglage fin de la LoRA actuellement largement utilisée sur les ensembles de données grand public.

• Article : PiSSA : Principales valeurs singulières et adaptation de vecteurs singuliers de grands modèles de langage

• Lien article : https://arxiv.org/pdf/2404.02948.pdf

• Lien code : https ://github.com/GraphPKU/PiSSA

La figure 1 montre que PiSSA (Figure 1c) est complètement cohérent avec LoRA [1] dans l'architecture du modèle (Figure 1b), mais la manière d'initialiser l'adaptateur est différente . LoRA initialise A avec du bruit gaussien et B avec des 0. PiSSA utilise des valeurs singulières principales et des vecteurs singuliers pour initialiser l'adaptateur afin d'initialiser A et B.

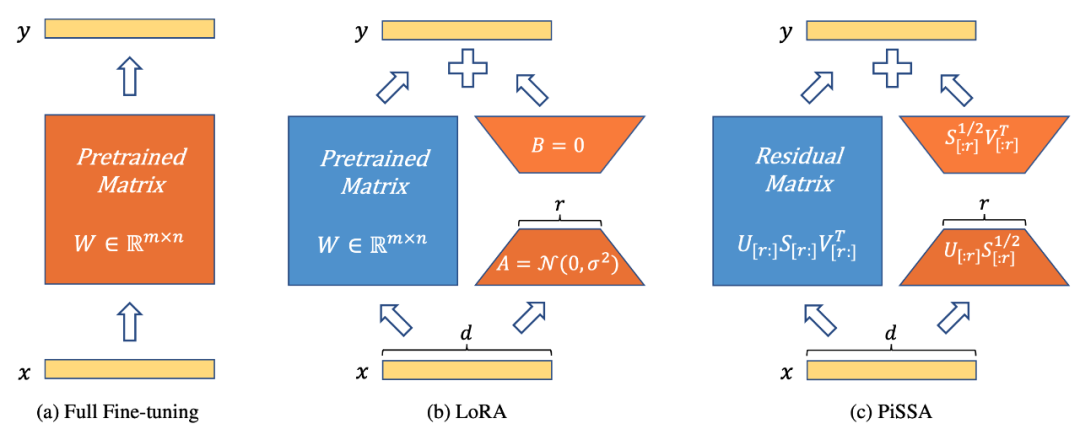
^{La figure 1 montre le réglage fin des paramètres complets, LoRA et PiSSA de gauche à droite. Le bleu représente les paramètres gelés, l'orange représente les paramètres pouvant être entraînés et d'autres méthodes d'initialisation. Par rapport au réglage fin de tous les paramètres, LoRA et PiSSA réduisent considérablement le nombre de paramètres pouvant être entraînés. Pour une même entrée, les sorties initiales de ces trois méthodes sont exactement égales. Cependant, PiSSA fige la partie secondaire du modèle et affine directement la partie principale (les premières r valeurs singulières et vecteurs singuliers) tandis que LoRA peut être considéré comme gelant la partie principale du modèle et affinant le bruit) ; partie.}

Comparez les effets de réglage fin de PiSSA et LoRA sur différentes tâches

L'équipe de recherche utilise Lama 2-7B, Mistral-7B et Gemma-7B comme modèles de base pour améliorer leurs capacités mathématiques, de codage et de dialogue grâce à réglage fin . Ceux-ci incluent : une formation sur MetaMathQA, vérifiant la capacité mathématique du modèle sur les ensembles de données GSM8K et MATH ; une formation sur CodeFeedBack, vérifiant la capacité de code du modèle sur les ensembles de données HumanEval et MBPP ; en utilisant MT -Vérifiez les capacités conversationnelles du modèle sur Bench. Comme le montrent les résultats expérimentaux du tableau ci-dessous, en utilisant la même échelle de paramètres pouvant être entraînés, l'effet de réglage fin de PiSSA dépasse considérablement LoRA, et dépasse même le réglage fin de tous les paramètres.

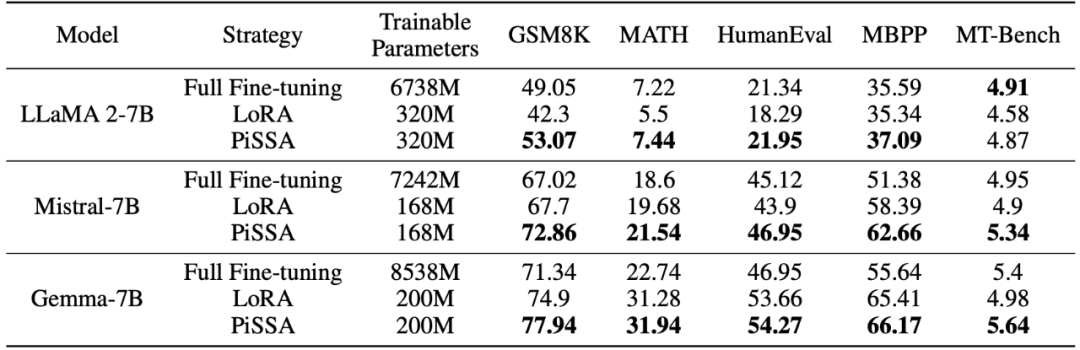
Comparaison des effets du réglage fin PiSSA et LoRA sous différentes quantités de paramètres pouvant être entraînés

L'équipe de recherche a mené des expériences d'ablation sur la relation entre la quantité de paramètres pouvant être entraînés et l'effet du modèle sur les tâches mathématiques. D'après la figure 2.1, on peut constater qu'au début de l'entraînement, la perte d'entraînement de PiSSA diminue très rapidement, tandis que LoRA a un stade où elle ne diminue pas ou même augmente légèrement. De plus, la perte d'entraînement de PiSSA est inférieure à celle de LoRA, ce qui indique qu'elle s'adapte mieux à l'ensemble d'entraînement. Les figures 2.2, 2.3 et 2.4 montrent que sous chaque paramètre, la perte de PiSSA est toujours inférieure à celle de LoRA et sa précision est. toujours supérieur à LoRA High, PiSSA peut rattraper l'effet d'un réglage fin complet des paramètres en utilisant moins de paramètres pouvant être entraînés.

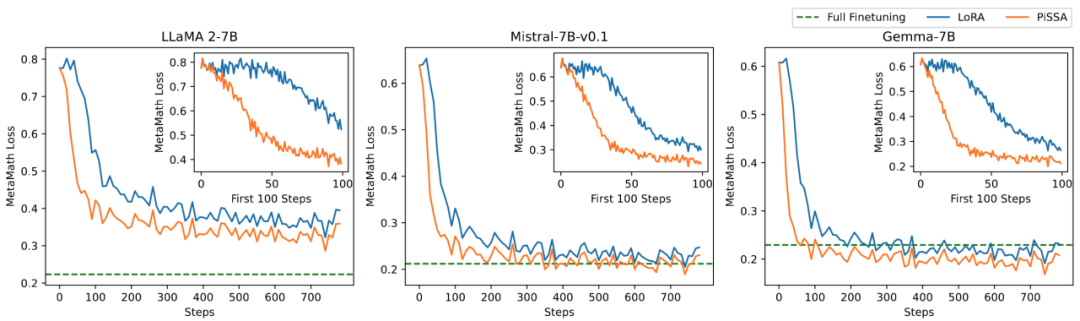
^{Figure 2.1) Lorsque le rang est 1, la perte de PiSSA et LoRA pendant le processus de formation. Le coin supérieur droit de chaque figure est la courbe agrandie des 100 premières itérations. Parmi eux, PiSSA est représenté par la ligne orange, LoRA est représentée par la ligne bleue et le réglage fin de tous les paramètres utilise la ligne verte pour montrer la perte finale comme référence. Le phénomène lorsque le rang est [2,4,8,16,32,64,128] est cohérent avec cela, voir l'annexe de l'article pour plus de détails.}

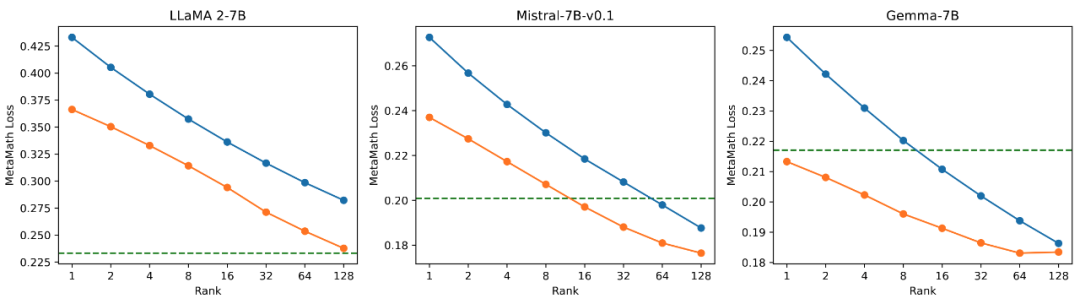
                                                                                                                                                                                                               ^{Figure 2.2) La perte d'entraînement finale de PiSSA et LoRA en utilisant les rangs [1,2,4,8,16,32,64,128].}

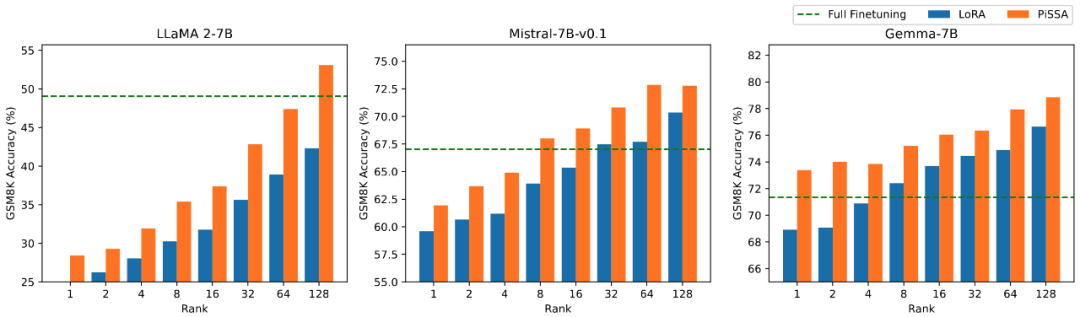
                                                                                                                                                                                                                           ^Précision.

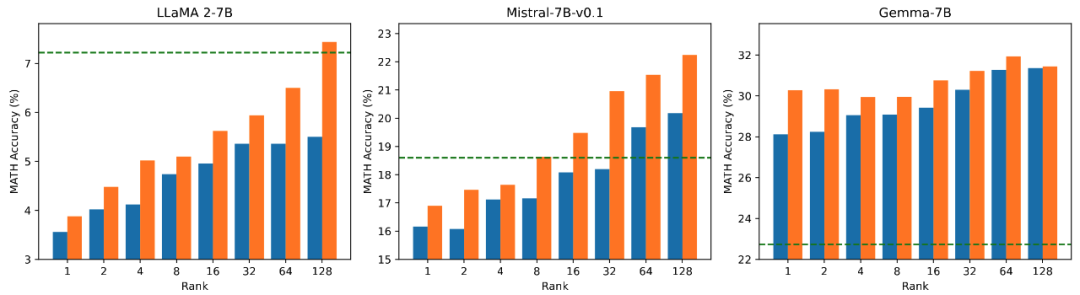
                                                                                                                                                                                                                ^{sur le taux de précision.}

Explication détaillée de la méthode PiSSA

Inspiré par Intrinsic SAID [2] "Les paramètres du grand modèle pré-entraîné ont un rang bas", PiSSA effectue une décomposition en valeurs singulières sur la matrice de paramètres 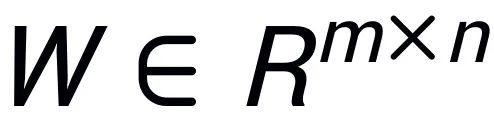du modèle pré-entraîné, où les r premières valeurs singulières et vecteurs singuliers sont utilisés pour initialiser l'adaptateur ) des deux matrices et , ; les valeurs singulières restantes et les vecteurs singuliers sont utilisés pour construire la matrice résiduelle , telle que 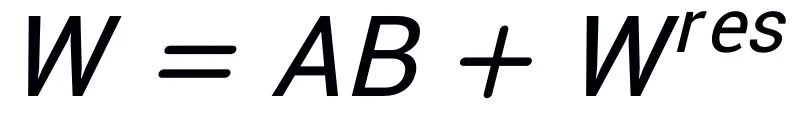. Par conséquent, les paramètres de l'adaptateur contiennent les paramètres de base du modèle, tandis que les paramètres de la matrice résiduelle sont des paramètres de correction. En affinant les adaptateurs de base A et B avec des paramètres plus petits et en gelant la matrice résiduelle avec des paramètres plus grands, l'effet d'un réglage fin approximatif de tous les paramètres avec très peu de paramètres est obtenu.

Bien qu'également inspirés par Intrinsic SAID [1], les principes derrière PiSSA et LoRA sont complètement différents.

LoRA estime que le changement de matrice △W avant et après réglage fin du grand modèle a un rang r intrinsèque très faible, donc le changement de modèle △W est simulé par la matrice de rang bas obtenue en multipliant et . Dans la phase initiale, LoRA initialise A avec un bruit gaussien et B avec 0, afin de garantir que la capacité initiale du modèle ne change pas, et ajuste A et B pour mettre à jour W. En revanche, PiSSA ne se soucie pas de △W, mais considère que W a un rang r intrinsèque très faible. Par conséquent, nous effectuons directement une décomposition en valeurs singulières sur W et la décomposons en composantes principales A, B et le terme résiduel , de sorte que . Supposons que la décomposition en valeurs singulières de W est 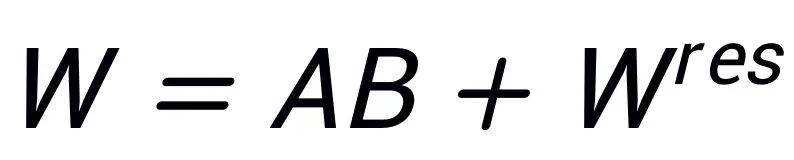, A et B sont initialisés en utilisant les r valeurs singulières et les vecteurs singuliers avec les plus grandes valeurs singulières après la décomposition SVD :

La matrice résiduelle est initialisée en utilisant les valeurs singulières et vecteurs singuliers restants :

PiSSA affine directement les composantes principales de bas rang A et B de W et fige les termes de correction mineurs. Par rapport à LoRA, qui utilise le bruit gaussien et 0 pour initialiser les paramètres de l'adaptateur et geler les paramètres du modèle de base, PiSSA converge plus rapidement et donne de meilleurs résultats.

PiSSA se prononce comme "pizza" --- Si l'on compare le grand modèle entier à une pizza complète, PiSSA coupe un coin, et c'est le coin avec les garnitures les plus riches (valeurs singulières principales, vecteurs singuliers), Re- cuire au four (mise au point des tâches en aval) selon votre goût préféré.

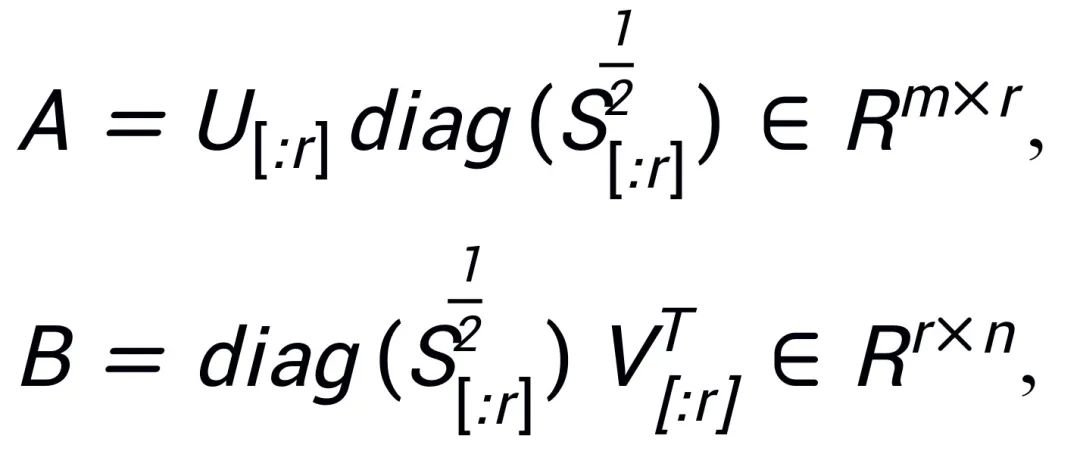
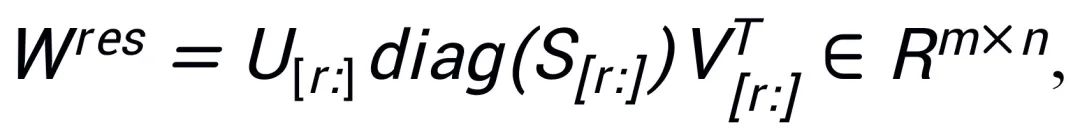
Étant donné que PiSSA adopte exactement la même architecture que LoRA, elle peut être utilisée comme méthode d'initialisation facultative pour LoRA et peut être facilement modifiée et appelée dans le package peft (comme indiqué dans le code suivant). La même architecture permet également à PiSSA d'hériter de la plupart des avantages de LoRA, tels que : l'utilisation de la quantification sur 4 bits [3] pour le modèle résiduel afin de réduire la surcharge de formation une fois le réglage fin terminé, l'adaptateur peut être fusionné dans le modèle résiduel ; modèle sans modifier l'architecture du modèle du processus d'inférence ; Il n'est pas nécessaire de partager les paramètres complets du modèle, seul le module PiSSA avec un petit nombre de paramètres doit être partagé. Les utilisateurs peuvent effectuer automatiquement la décomposition et l'affectation de valeurs singulières en chargeant directement le modèle. Module PiSSA ; un modèle peut utiliser plusieurs modules PiSSA en même temps, etc. Certaines améliorations de la méthode LoRA peuvent également être combinées avec PiSSA : par exemple, au lieu de fixer le classement de chaque couche, trouver le meilleur classement grâce à l'apprentissage [4] en utilisant des mises à jour guidées par PiSSA [5] pour dépasser la limite de classement, etc.

# 在 peft 包中 LoRA 的初始化方式后面增加了一种 PiSSA 初始化选项：if use_lora:nn.init.normal_(self.lora_A.weight, std=1 /self.r)nn.init.zeros_(self.lora_B.weight) elif use_pissa:Ur, Sr, Vr = svd_lowrank (self.base_layer.weight, self.r, niter=4) # 注意：由于 self.base_layer.weight 的维度是 (out_channel,in_channel, 所以 AB 的顺序相比图示颠倒了一下)self.lora_A.weight = torch.diag (torch.sqrt (Sr)) @ Vh.t ()self.lora_B.weight = Ur @ torch.diag (torch.sqrt (Sr))   self.base_layer.weight = self.base_layer.weight - self.lora_B.weight @ self.lora_A.weight

Expérience de comparaison des effets de réglage fin des valeurs singulières élevées, moyennes et faibles

Afin de vérifier l'impact de l'utilisation de différentes tailles de valeurs singulières et de vecteurs singuliers pour initialiser l'adaptateur sur le modèle, les chercheurs ont utilisé des valeurs singulières élevées, moyennes et faibles pour initialiser respectivement LLaMA 2-7B, Mistral-7B-v0.1, l'adaptateur Gemma-7B, puis affiné sur l'ensemble de données MetaMathQA, et les résultats expérimentaux sont. illustré à la figure 3. Comme le montre la figure, la méthode utilisant l'initialisation de la valeur singulière primaire présente la plus petite perte de formation et a une plus grande précision sur les ensembles de validation GSM8K et MATH. Ce phénomène vérifie l'efficacité du réglage fin des principales valeurs singulières et vecteurs singuliers.

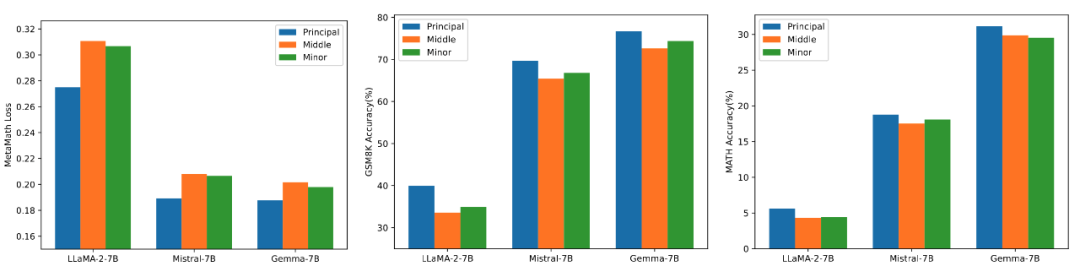
^{Figure 3) De gauche à droite se trouvent la perte d'entraînement, la précision sur GSM8K et la précision sur MATH. Le bleu représente la valeur singulière maximale, l'orange représente la valeur singulière moyenne et le vert représente la valeur singulière minimale.}

Décomposition rapide des valeurs singulières

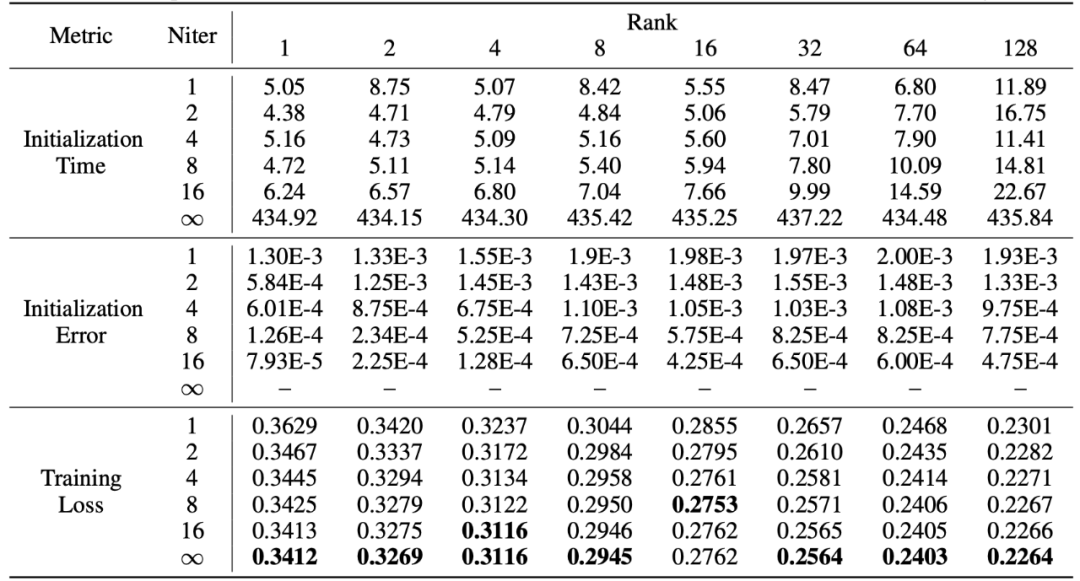
PiSSA hérite des avantages de LoRA, est facile à utiliser et a de meilleurs effets que LoRA. Le prix est que pendant la phase d'initialisation, le modèle doit être décomposé en valeurs singulières. Bien qu’il ne doive être décomposé qu’une seule fois lors de l’initialisation, cela peut néanmoins nécessiter plusieurs minutes, voire plusieurs dizaines de minutes de temps système. Par conséquent, les chercheurs ont utilisé une méthode de décomposition rapide en valeurs singulières [6] pour remplacer la décomposition SVD standard. Comme le montrent les expériences du tableau ci-dessous, il ne faut que quelques secondes pour se rapprocher de l'effet d'ajustement de l'ensemble d'apprentissage du SVD standard. décomposition. Niter représente le nombre d'itérations. Plus le Niter est grand, plus le temps est long mais plus l'erreur est petite. Niter = ∞ représente le SVD standard. L'erreur moyenne dans le tableau représente la distance moyenne L_1 entre A et B obtenue par décomposition rapide en valeurs singulières et SVD standard.

Résumé et perspectives

Ce travail effectue une décomposition en valeurs singulières sur les poids du modèle pré-entraîné. En utilisant les paramètres les plus importants pour initialiser un adaptateur nommé PiSSA, le réglage fin de cet adaptateur se rapproche du réglage fin. le modèle complet. Les expériences montrent que PiSSA converge plus rapidement que LoRA et donne de meilleurs résultats finaux. Le seul coût est le processus d'initialisation du SVD qui prend plusieurs secondes.

Alors, pour de meilleurs résultats d'entraînement, êtes-vous prêt à passer quelques secondes de plus et à changer l'initialisation de LoRA en PiSSA en un seul clic ?

^Références

^{[1] LoRA : Adaptation de bas rang de grands modèles de langage}

^{[2] La dimensionnalité intrinsèque explique l'efficacité du réglage fin du modèle de langage}

^{[3] QLoRA : réglage fin efficace des LLM quantifiés}

^{[4] AdaLoRA : allocation budgétaire adaptative pour un réglage fin efficace des paramètres}

^{[5] Delta-LoRA : réglage fin de haut rang Paramètres avec le delta des matrices de bas rang}

^{[6] Trouver une structure aléatoire : algorithmes probabilistes pour la construction de décompositions matricielles approximatives}

Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!