Étapes détaillées pour réaliser une animation de démonstration du théorème de l'angle circonférentiel sur le carnet de croquis géométrique

L'éditeur PHP Strawberry vous dévoile la nouvelle expérience de jeu de Winter Rhapsody ! Ce jeu de simulation d'intrigue de personnages se déroulant dans l'histoire d'une petite ville intègre des éléments japonais et les joueurs seront confrontés à divers défis approfondis de résolution d'énigmes. L'utilisation des compétences devient essentielle et le déverrouillage de toutes les compétences vous offrira une expérience de jeu plus complète. Êtes-vous prêt à découvrir un contenu spécial passionnant et un gameplay riche basé sur les compétences ?

Théorème de l'angle circonférentiel : L'angle circonférentiel sous-tendu par un arc est égal à la moitié de l'angle qu'il sous-tend au centre du cercle.

L'opération spécifique est la suivante :

Utilisez "l'outil Cercle" pour dessiner un cercle O, puis utilisez "l'outil Point" pour choisir trois points A, B et P sur le cercle, sélectionnez les points B, A et encerclez O à tour de rôle, et exécutez "Construction" »——La commande « Arc sur cercle » construit l'arc AB. Utilisez l'outil de segment de ligne pour construire des segments de ligne OA, OB, PA et PB, et créez l'angle circonférentiel et l'angle central. Notez que les arcs auxquels ils correspondent sont les mêmes.

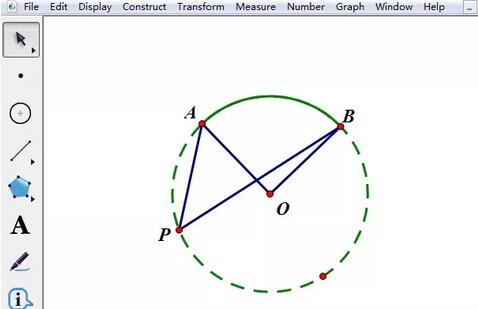
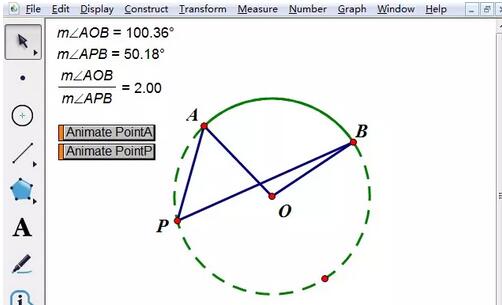
Mesure l'angle central et l'angle circonférentiel en degrés. Sélectionnez trois points A, O et B dans l'ordre, exécutez la commande [Mesure]-[Angle], et la taille de ∠AOB sera affichée immédiatement dans le coin supérieur gauche de la planche à dessin. La taille de ∠APB peut être. mesuré de la même manière. Une fois cela fait, vous pouvez effectuer une démonstration manuelle.

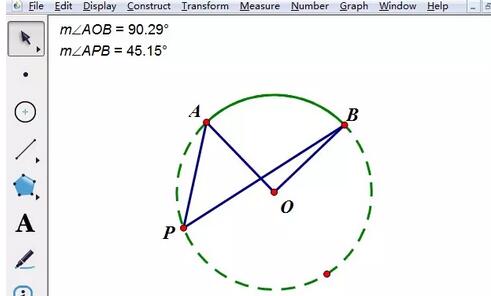
À ce stade, faites une démonstration manuelle du didacticiel et utilisez la souris pour déplacer la position du point P. Les degrés des deux angles ne changeront pas et ∠AOB est deux fois plus élevé que ∠APB. Par conséquent, lorsque ∠AOB est fixé, le théorème est établi. Les élèves peuvent alors se demander : si la taille de ∠AOB est modifiée, y aura-t-il toujours cette relation quantitative entre ces deux angles ?

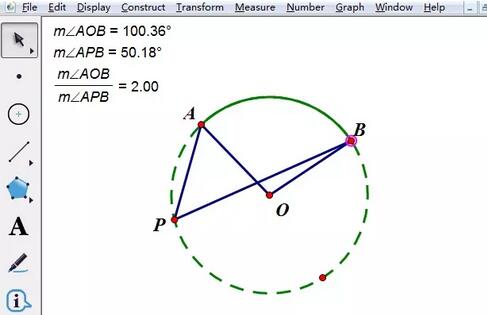
Calculez les valeurs. Exécutez la commande [Data]-[Calculate] pour calculer la valeur de ∠AOB/∠APB. À ce moment, déplacez la position du point B et changez la taille de ∠AOB. La valeur de ∠AOB/∠APB est toujours égale à 2. Cela signifie que lorsque la taille de ∠AOB change, ∠APB est toujours la moitié de ∠. AOB.

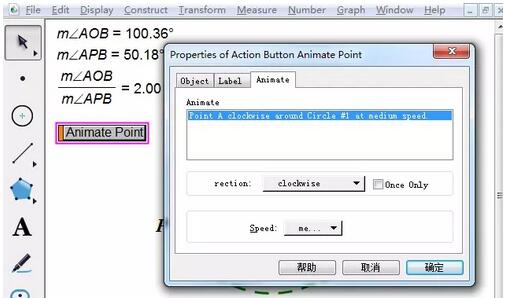
Animation des points de consigne. Les démonstrations manuelles ont des limites de localisation et sont difficiles à convaincre les étudiants. Par conséquent, pour définir une animation de point, définissez d'abord l'animation du point mobile A, sélectionnez le point A et exécutez la commande [Modifier]-[Bouton d'opération]-[Animation] Définissez les propriétés spécifiques comme indiqué dans la figure ci-dessous, cliquez sur. le bouton d'animation, on peut voir que peu importe la façon dont les degrés des deux angles changent, leur rapport est toujours de 2 et ne change pas.

Définissez l'animation d'un autre point P, indiquant que peu importe la façon dont le point P se déplace sur le cercle, le rapport est de 2. La méthode de paramétrage est la même que ci-dessus. Insistez simplement sur le fait que si vous souhaitez modifier l'étiquette, cliquez sur l'étiquette et nommez-la point d'animation P.

Exemple de création d'animation en cliquant sur le bouton P Utiliser et enregistrer l'animation. Le didacticiel est prêt. Cliquez sur le bouton d'animation du point P pour expliquer que quelle que soit la façon dont le point P change de position, le degré de l'angle circonférentiel est toujours égal au degré de l'angle central du cercle opposé au même arc. Cliquez sur le bouton du point d'animation A. Quelle que soit la façon dont ∠AOB change, le degré de l'angle circonférentiel ∠APB est toujours égal à la moitié de celui-ci. Enfin, exécutez la commande [Fichier]-[Enregistrer sous] pour enregistrer le fichier, qui peut être inséré dans PPT ou utilisé seul.

Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!