 Tutoriel logiciel
Tutoriel logiciel
 Logiciel
Logiciel
 Comment dessiner des figures géométriques selon des conditions connues dans le carnet de croquis géométrique
Comment dessiner des figures géométriques selon des conditions connues dans le carnet de croquis géométrique
Comment dessiner des figures géométriques selon des conditions connues dans le carnet de croquis géométrique
Par exemple, on sait que dans le trapèze ABCD, AD∥BC, AB=AD+BC et E est le milieu de CD. Prouver : AE et BE coupent respectivement ∠BAD et ∠ABC.
Nous pouvons partir des conditions connues et suivre les étapes suivantes pour dessiner une figure qui répond au sens de la question sur le carnet de croquis géométrique.
Ouvrez le carnet de croquis géométrique, utilisez l'[Outil Point] pour dessiner deux points A et B dans l'espace vide du carnet de croquis, sélectionnez l'[Outil Rayon] pour dessiner des rayons horizontaux passant par les points A et B respectivement, et sélectionnez les points A et B pour construire des segments de droite.
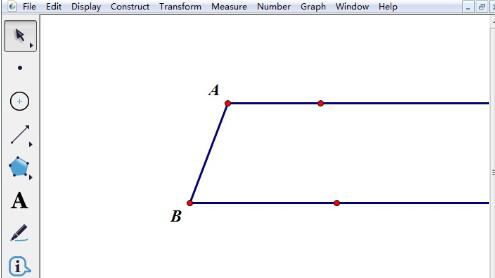
Utilisez l'[Outil Point] pour choisir un point F sur le segment de ligne AB, prenez les points A et B comme points centraux et utilisez les longueurs AF et BF comme rayons pour dessiner des cercles avec les rayons. les deux bases se coupent aux points D et C. Évidemment, AD+BC=AB.
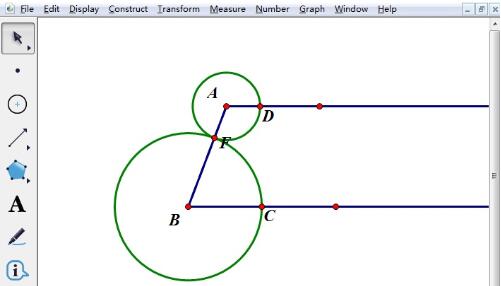
Prenez le milieu E du segment de ligne CD et connectez AE et BE. Sélectionnez les points C et D, exécutez la commande [Construct]-[Midpoint] pour dessiner le point médian E, sélectionnez les points A, E, B et E en séquence, exécutez la commande [Construct]-[Line Segment] pour obtenir la ligne segments AE, BE.
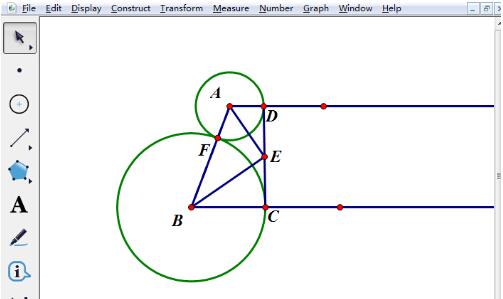
Masquez les graphiques auxiliaires pendant le processus de dessin pour obtenir des graphiques qui répondent aux exigences de la question. Sélectionnez les rayons et cercles inutiles et appuyez sur la touche de raccourci [Ctrl+H] pour masquer les objets inutiles et obtenir un graphique qui combine le sens de la question comme le montre la figure.
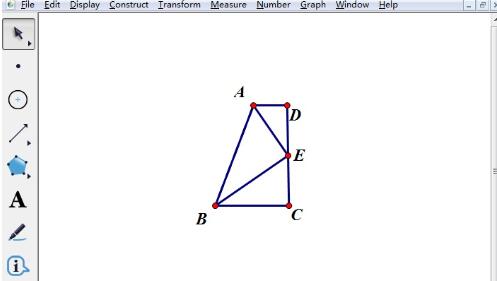
Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!

Outils d'IA chauds

Undresser.AI Undress
Application basée sur l'IA pour créer des photos de nu réalistes

AI Clothes Remover
Outil d'IA en ligne pour supprimer les vêtements des photos.

Undress AI Tool
Images de déshabillage gratuites

Clothoff.io
Dissolvant de vêtements AI

AI Hentai Generator
Générez AI Hentai gratuitement.

Article chaud

Outils chauds

Bloc-notes++7.3.1
Éditeur de code facile à utiliser et gratuit

SublimeText3 version chinoise
Version chinoise, très simple à utiliser

Envoyer Studio 13.0.1
Puissant environnement de développement intégré PHP

Dreamweaver CS6
Outils de développement Web visuel

SublimeText3 version Mac
Logiciel d'édition de code au niveau de Dieu (SublimeText3)
 Comment corriger: err_response_headers_multiple_access_control_allow_origin Erreur dans Google Chrome
Mar 21, 2025 pm 06:19 PM
Comment corriger: err_response_headers_multiple_access_control_allow_origin Erreur dans Google Chrome
Mar 21, 2025 pm 06:19 PM
L'article discute de la correction de l'erreur "ERR_RESPESONS_HEADERS_MULTIPLE_ACCESS_CONTROL_ALLOW_ORIGIN" en chrome en abordant plusieurs en-têtes d'accès à l'origine.
 Combien coûte Microsoft PowerToys?
Apr 09, 2025 am 12:03 AM
Combien coûte Microsoft PowerToys?
Apr 09, 2025 am 12:03 AM
Microsoft PowerToys est gratuit. Cette collection d'outils développée par Microsoft est conçue pour améliorer les fonctions du système Windows et améliorer la productivité des utilisateurs. En installant et en utilisant des fonctionnalités telles que FancyZones, les utilisateurs peuvent personnaliser les dispositions de fenêtres et optimiser les workflows.
 Comment corriger: err_incomplete_chunked_encoding Erreur dans Google Chrome
Mar 21, 2025 pm 06:02 PM
Comment corriger: err_incomplete_chunked_encoding Erreur dans Google Chrome
Mar 21, 2025 pm 06:02 PM
L'article traite de l'erreur "err_incomplete_chunked_encoding" dans Google Chrome, offrant des correctifs comme le rechargement de la page, la nettoyage du cache et la désactivation des extensions. Il explore également les causes communes et les mesures préventives.
 Quel est le but de PowerToys?
Apr 03, 2025 am 12:10 AM
Quel est le but de PowerToys?
Apr 03, 2025 am 12:10 AM
PowerToys est une collection gratuite d'outils lancés par Microsoft pour améliorer la productivité et le contrôle du système pour les utilisateurs de Windows. Il fournit des fonctionnalités via des modules autonomes tels que la disposition des fenêtres de gestion des fraîches et les fichiers de renommage par lots PowerRename, ce qui rend le flux de travail des utilisateurs plus fluide.
 Comment corriger: ERR_RESPONSE_HEADERS_MULTIPLE_LOCATION Erreur dans Google Chrome
Mar 21, 2025 pm 06:05 PM
Comment corriger: ERR_RESPONSE_HEADERS_MULTIPLE_LOCATION Erreur dans Google Chrome
Mar 21, 2025 pm 06:05 PM
L'article traite de l'erreur "ERR_RESPONSE_HEADERS_MULTIPLE_LOCATION" dans Google Chrome, causée par des serveurs envoyant plusieurs en-têtes de localisation. Il fournit des solutions comme rafraîchir la page, effacer le cache, désactiver les extensions et vérifier
 PowerToys doit-il fonctionner?
Apr 02, 2025 pm 04:41 PM
PowerToys doit-il fonctionner?
Apr 02, 2025 pm 04:41 PM
PowerToys doit être exécuté en arrière-plan pour atteindre sa pleine fonctionnalité. 1) Il s'appuie sur des crochets au niveau du système et l'écoute des événements, tels que le mouvement des fenêtres de surveillance de FancyZones. 2) Utilisation raisonnable des ressources, généralement 50-100 Mo de mémoire, et presque zéro utilisation du processeur en cas d'inactivité. 3) Vous pouvez configurer la mise sous tension et utiliser des scripts PowerShell pour l'implémenter. 4) Lorsque vous rencontrez des problèmes, vérifiez les fichiers journaux, désactivez les outils spécifiques et assurez-vous qu'ils sont mis à jour vers la dernière version. 5) Les suggestions d'optimisation incluent la désactivation des outils rarement utilisés, l'ajustement des paramètres et la surveillance de l'utilisation des ressources.
 Comment corriger: err_timed_out Erreur dans Google Chrome
Mar 26, 2025 am 11:45 AM
Comment corriger: err_timed_out Erreur dans Google Chrome
Mar 26, 2025 am 11:45 AM
L'article discute de la correction de l'erreur "err_timed_out" dans Google Chrome, causée par un mauvais Internet, des problèmes de serveur, des problèmes DNS, etc. Offre des solutions comme la vérification de la connexion, la compensation du cache et la réinitialisation des paramètres.
 Quelle est la meilleure alternative à PowerToys?
Apr 08, 2025 am 12:17 AM
Quelle est la meilleure alternative à PowerToys?
Apr 08, 2025 am 12:17 AM
TheBestalternatiVestOpowerToySforwindowSersaReAutoHotkey, Windowgrid, andwinaerotweaker.1) AutoHotKeyOffersExtensivesScriptingForAutomation.2) WindowgridProvidesInSitiveGrid-basez-basywindowmanagement.3)





