Le blog Google a publié de nouvelles recherches pour résoudre le problème de coupe minimale des graphiques non orientés.
En 1996, l'informaticien américain David R Karger et d'autres chercheurs ont proposé un surprenant algorithme aléatoire de Karger dans l'article "Une nouvelle approche du problème de coupe minimale", très populaire en informatique théorique. très important, particulièrement adapté aux problèmes de coupe minimale approximative sur des graphiques à grande échelle. L'algorithme de Karger peut trouver un point de coupure minimum dans un graphique dans le temps O (m log^3n), qu'ils appellent temps presque linéaire, c'est-à-dire multiplication linéaire par un facteur polylogarithmique. Dans un blog récemment mis à jour par Google, ils ont présenté un article précédemment publié "Deterministic Near-Linear Time Minimum Cut in Weighted Graphs", et la recherche a remporté le prix ACM-SIAM SODA24 du meilleur article. L'article détaille un nouvel algorithme qui s'exécute dans un temps presque linéaire (plutôt qu'un temps presque linéaire). Cet algorithme est déterministe et peut trouver de manière fiable la coupe minimale correcte. Il améliore l'algorithme précédent dont l'exactitude n'est peut-être pas garantie ou qui s'applique uniquement à. Algorithmes pour graphiques simples. Il s’agit sans doute de la plus grande découverte depuis le célèbre algorithme de randomisation de Karger.
- Adresse du papier: https://arxiv.org/pdf/2401.05627.pdf
- Titre: Temps quasi-linéaire déterministe coupe minimum dans les graphiques pondérés
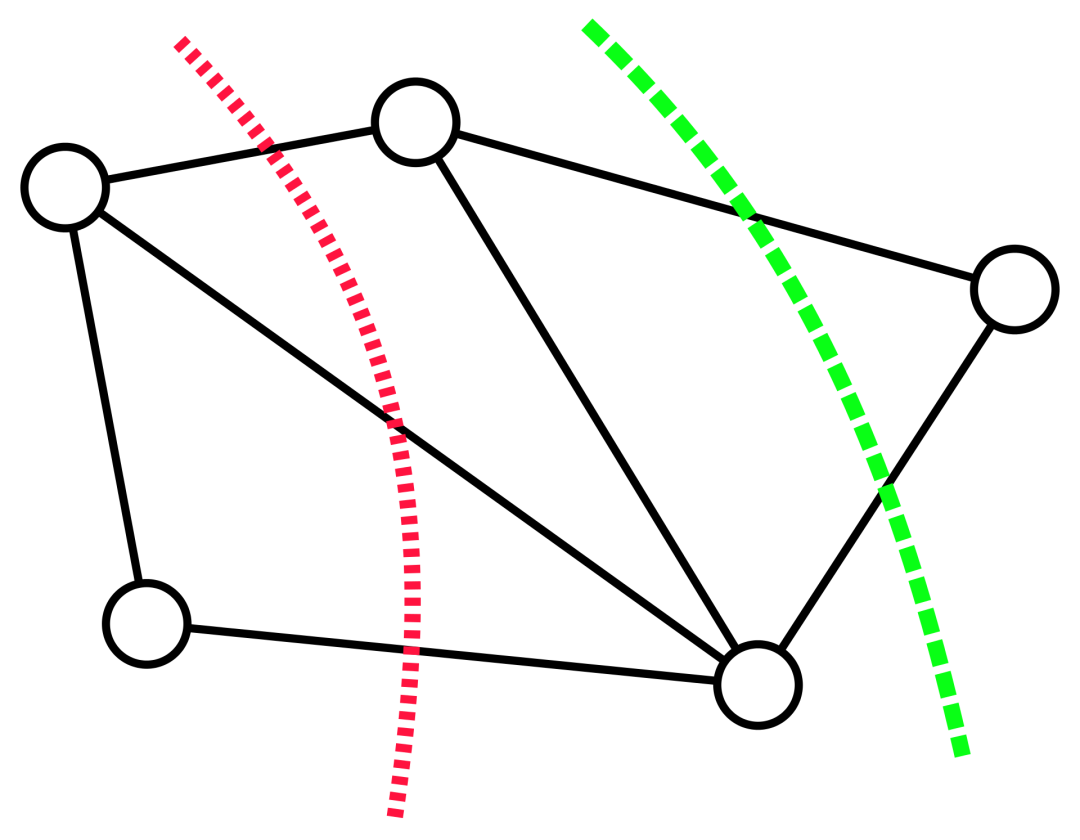
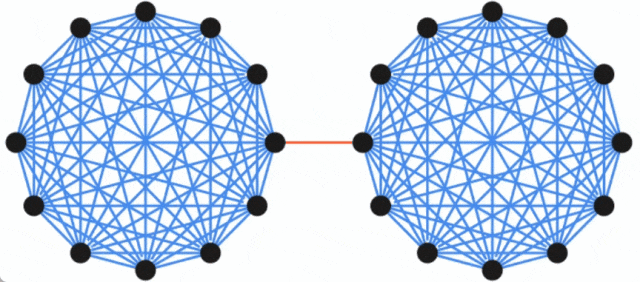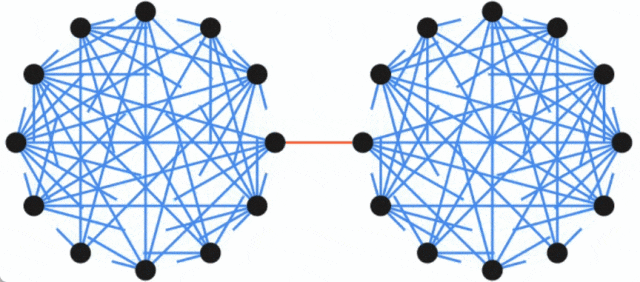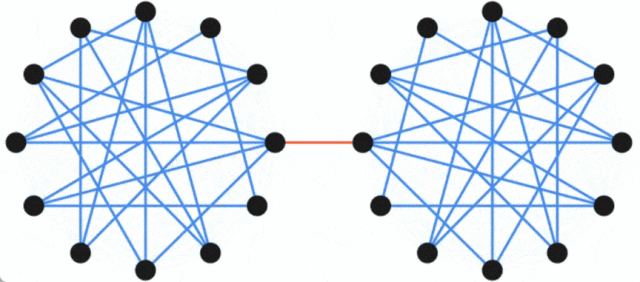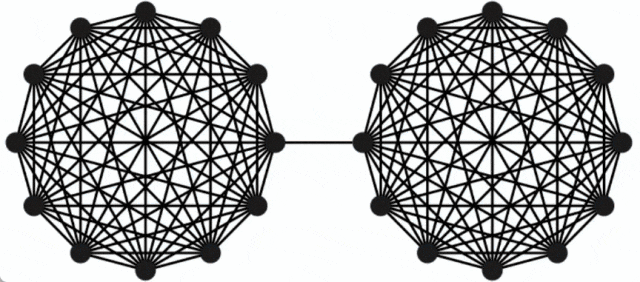
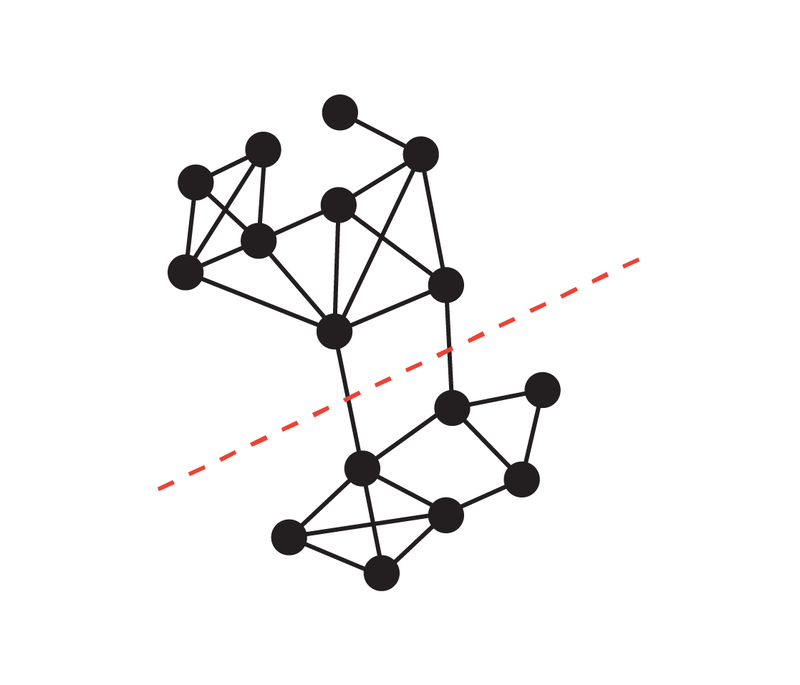
Not: le plus petit Le problème de coupure (souvent appelé coupure minimale) est un problème structurel de base concernant la connectivité des graphiques. Il se concentre généralement sur le moyen le plus simple de déconnecter le réseau ? Dans la théorie des graphes, l'ensemble des arêtes qui peuvent rendre un graphe de flux de réseau plus connecté (c'est-à-dire divisé en deux sous-graphes) en supprimant toutes les arêtes est appelé une coupe du graphe, et la plus petite coupe sur un graphe est appelée une coupe minimale. Un graphe et ses deux coupes : la ligne pointillée rouge marque une coupe contenant trois arêtes, et la ligne pointillée verte représente une coupe minimale (incluant deux arêtes) de ce graphe. Introduction à la méthode Concernant le problème de la coupe minimale, Karger a été le pionnier d'un algorithme aléatoire temporel presque linéaire, qui peut trouver la coupe minimale avec une forte probabilité, et le travail donne également. un élément clé est qu'il existe un graphique plus petit qui préserve en grande partie la taille de toutes les coupes. Cette découverte est utile car des algorithmes plus lents peuvent être exécutés en utilisant des graphiques plus petits en entrée, et le temps d'exécution plus lent (en termes de taille du graphique plus petit) est toujours comparable à l'original (Plus grand) La taille du le graphique est presque linéaire. En fait, de nombreuses découvertes structurelles sur le problème de la coupe minimale sont réalisées dans cette direction. Google fait cela, en partant d'un graphe G avec n nœuds, puis en se basant sur la méthode de préservation des coupures proposée dans l'article "Schémas d'approximation aléatoire pour les coupes et les flux dans les graphes capacitaires" (écrit par Benzur, Karger ) , prouve qu'un graphe à pondération clairsemée G' avec moins d'arêtes peut être construit, et sur ce graphe, la taille de presque toutes les coupes est à peu près la même que la taille des coupes correspondantes dans le graphe d'origine G. Ce concept peut être illustré par l'exemple suivant : le graphe original est constitué de deux graphes complets reliés par une seule arête, tandis que le graphe sparsifié a moins d'arêtes, mais le poids des arêtes est plus grand, et en même temps temps toutes les coupes La taille est à peu près préservée. 
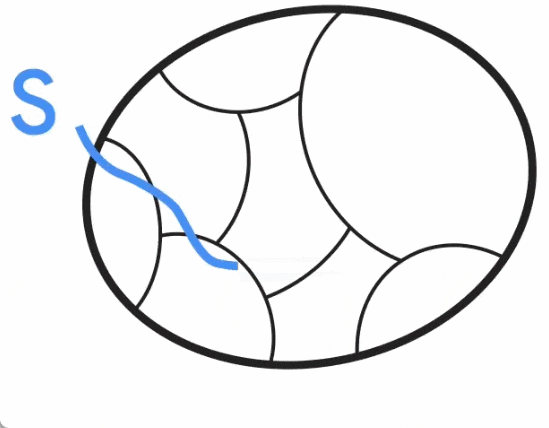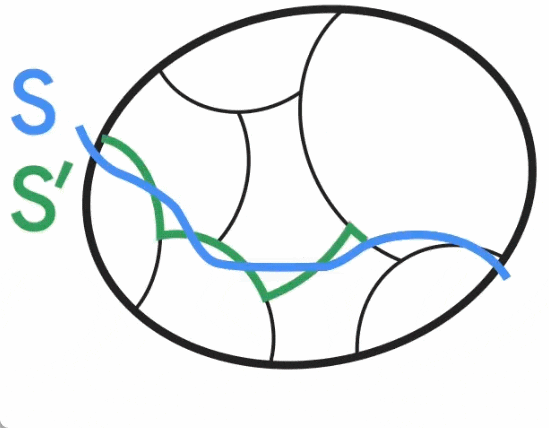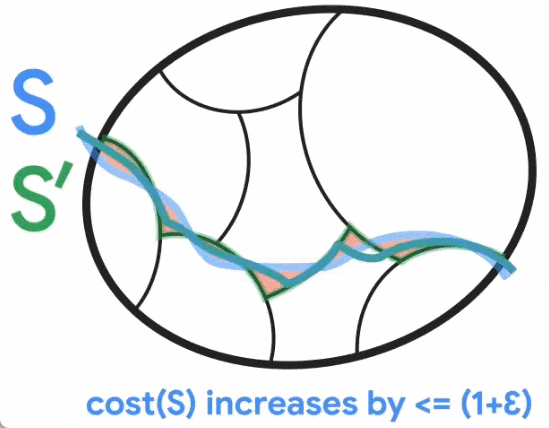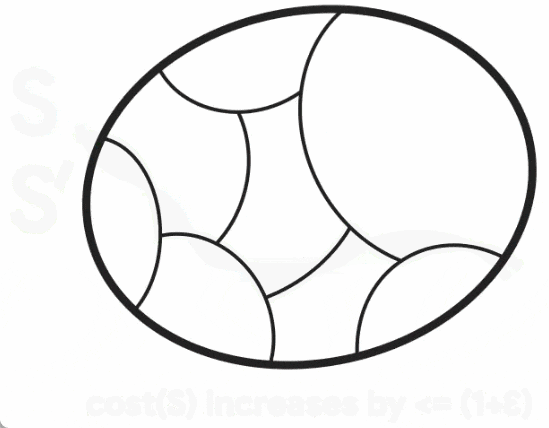
Pour construire ce graphe plus clairsemé, Benzur et Karger ont adopté la méthode d'échantillonnage indépendant des bords. Dans cette méthode, chaque arête du graphe G a une certaine probabilité d'être incluse dans le graphe G', et son poids dans G' sera amplifié selon l'inverse de la probabilité d'échantillonnage (par exemple, si le poids d'origine d'une arête est 1 L'arête est incluse avec une probabilité de 10 %, puis son poids est ajusté à 10). Il s’avère que cette approche très simple (dans le temps presque linéaire) peut construire des sparsifications de graphiques préservant les coupures avec une forte probabilité de succès. Cependant, l'algorithme de Karger est un algorithme de Monte Carlo, c'est-à-dire que la sortie peut être incorrecte avec une faible probabilité, et il n'existe aucun moyen connu de savoir si la sortie est correcte autre que de la comparer à une coupe minimale connue réelle. . Par conséquent, les chercheurs ont travaillé dur pour explorer les moyens de résoudre le problème ouvert des algorithmes déterministes temporels quasi-linéaires. Puisque la construction d'une sparsification de graphe préservant les coupures est la seule composante stochastique de l'algorithme de Karger, une approche consiste à trouver une construction déterministe de la sparsification en temps quasi-linéaire (également appelée dérandomisation). En 2015, Kawarabayashi et Thorup ont franchi une étape importante : trouver un algorithme temporel déterministe quasi-linéaire pour les graphiques simples (c'est-à-dire des graphiques avec au plus une arête entre chaque paire de nœuds et tous les poids d'arête sont égaux à 1). L'étude mène à une idée clé, à savoir qu'il existe des liens entre les coupes minimales et une autre structure graphique importante (appelée « coupe à faible conductance »). Cette connexion a été cruciale pour dérandomiser ultérieurement l'algorithme de Karger sur des graphiques généraux pondérés par les bords et a aidé Google à dériver son nouvel algorithme. Alignement de la coupe minimale et de la coupe à faible conductanceLa conductance de la coupe graphique S est définie comme le rapport de la taille de coupe de S au volume de S (en supposant que S est le côté plus petit volume de la coupe et n'est pas vide), où le volume de S est le degré des nœuds dans S. la faible conductance de la coupe S capture intuitivement le goulot d'étranglement dans le réseau, puisque seul un petit nombre d'arêtes (par rapport à son volume) connectent S au reste du graphique. La conductance d'un graphique est définie comme la conductance minimale pour toute coupure dans le graphique, et les graphiques avec une conductance élevée (également appelés graphiques étendus) sont dits bien connectés car il n'y a pas de goulots d'étranglement à l'intérieur.  Kawayabarashi et Thorup ont observé que dans les graphiques simples avec de grands degrés de nœuds minimum, toute coupe minimale non triviale (c'est-à-dire au moins deux nœuds de chaque côté) doit avoir une faible conductance. Sur la base de cette observation, si le graphique peut être partitionné en clusters bien connectés, alors le partitionnement doit être cohérent avec chaque coupe minimale non triviale, puisque chaque cluster doit se trouver exactement d'un côté de chaque coupe. Ensuite, chaque cluster est réduit à un nœud et un graphe plus petit est traité où toutes les coupes minimales non triviales du graphe d'origine sont intactes. Cependant, pour les graphiques pondérés, l'observation ci-dessus n'est plus valable, et le même partitionnement utilisé dans le cas des graphiques simples peut ne pas être exactement cohérent avec les coupes minimales non triviales. Comme le montre la figure ci-dessous, Jason Li a observé en 2021 que cette division est encore à peu près conforme à la coupe minimale non triviale. En particulier, pour une coupe minimale non triviale S, il existe une coupe S' similaire à S telle que S' soit cohérente avec le cluster. Jason Li a en outre observé que cette propriété de partitionnement peut être exploitée pour dérandomiser efficacement la construction de la rareté des graphiques préservant les coupures.
Kawayabarashi et Thorup ont observé que dans les graphiques simples avec de grands degrés de nœuds minimum, toute coupe minimale non triviale (c'est-à-dire au moins deux nœuds de chaque côté) doit avoir une faible conductance. Sur la base de cette observation, si le graphique peut être partitionné en clusters bien connectés, alors le partitionnement doit être cohérent avec chaque coupe minimale non triviale, puisque chaque cluster doit se trouver exactement d'un côté de chaque coupe. Ensuite, chaque cluster est réduit à un nœud et un graphe plus petit est traité où toutes les coupes minimales non triviales du graphe d'origine sont intactes. Cependant, pour les graphiques pondérés, l'observation ci-dessus n'est plus valable, et le même partitionnement utilisé dans le cas des graphiques simples peut ne pas être exactement cohérent avec les coupes minimales non triviales. Comme le montre la figure ci-dessous, Jason Li a observé en 2021 que cette division est encore à peu près conforme à la coupe minimale non triviale. En particulier, pour une coupe minimale non triviale S, il existe une coupe S' similaire à S telle que S' soit cohérente avec le cluster. Jason Li a en outre observé que cette propriété de partitionnement peut être exploitée pour dérandomiser efficacement la construction de la rareté des graphiques préservant les coupures. 
Le nouvel algorithme conçu par Google vise à construire une partition pour formuler le cas d'utilisation du min-cut. L'étude de Google est plus précise et plus rapide que les méthodes plus générales et disponibles dans le commerce que Jason Li a utilisées dans ses travaux précédents. La nouvelle recherche optimise le temps d'exécution tout en garantissant la précision, et aboutit finalement à un algorithme déterministe en temps quasi-linéaire pour le problème de coupe minimale. Lien de référence : https://research.google/blog/solving-the-minimum-cut-problem-for-undirected-graphs/Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!


 Comment flasher le téléphone Xiaomi
Comment flasher le téléphone Xiaomi
 Comment centrer un div en CSS
Comment centrer un div en CSS
 Comment ouvrir un fichier rar
Comment ouvrir un fichier rar
 Méthodes de lecture et d'écriture de fichiers Java DBF
Méthodes de lecture et d'écriture de fichiers Java DBF
 Comment résoudre le problème de l'absence du fichier msxml6.dll
Comment résoudre le problème de l'absence du fichier msxml6.dll
 Formules de permutation et de combinaison couramment utilisées
Formules de permutation et de combinaison couramment utilisées
 Numéro de téléphone mobile virtuel pour recevoir le code de vérification
Numéro de téléphone mobile virtuel pour recevoir le code de vérification
 album photo dynamique
album photo dynamique