Comment utiliser le carnet de croquis géométrique pour faire pivoter une pyramide triangulaire

La pyramide triangulaire est une figure tridimensionnelle courante dans les figures géométriques, et il est souvent nécessaire de la faire pivoter pendant l'étude et le travail. L'éditeur PHP Yuzai a appris que dans le carnet de croquis géométrique, il n'est pas compliqué de réaliser l'opération de rotation de la vertèbre triangulaire. Cet article présentera en détail les étapes spécifiques pour aider chacun à maîtriser facilement cette technique. Lisez la suite pour savoir comment faire pivoter une pyramide triangulaire dans Geometry Sketchpad.

1. Utilisez l'outil Cercle pour dessiner deux cercles concentriques de centre A. Utilisez l'outil Point pour choisir un B et un C sur les deux cercles. Dessinez tous les points D et E sur la circonférence du grand cercle, tracez les segments de ligne AD et AE et coupez le petit cercle aux points F et G respectivement.

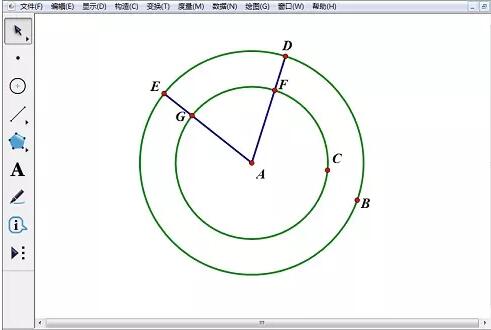
2. Double-cliquez sur le point A et marquez A comme centre de rotation. Sélectionnez les points E et G, sélectionnez la commande [Transformer]-[Rotate] et définissez l'angle fixe sur 120 degrés. Cliquez sur OK]. Faites la même transformation pour les points E’ et G’.

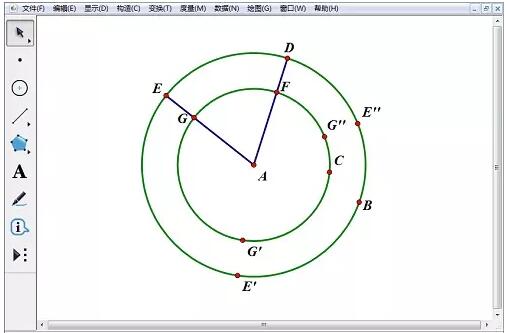
3. Sélectionnez les points E, E', E'' et le segment de ligne AD, sélectionnez la commande [Construction]-[Ligne verticale], définissez les trois lignes verticales comme lignes pointillées et nommez-les j, k et je respectivement.

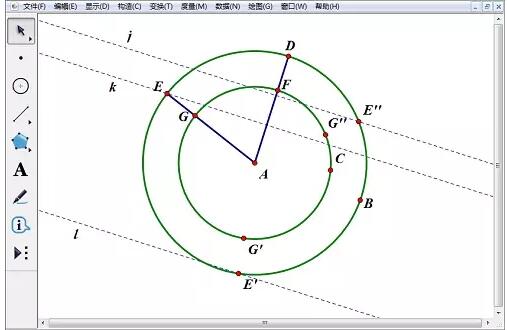
4. Sélectionnez les points G, G', G'' et le segment de ligne AD, sélectionnez la commande [Construction]-[Lignes parallèles], définissez les trois lignes verticales comme lignes pointillées et nommez-les m, n, o. respectivement.

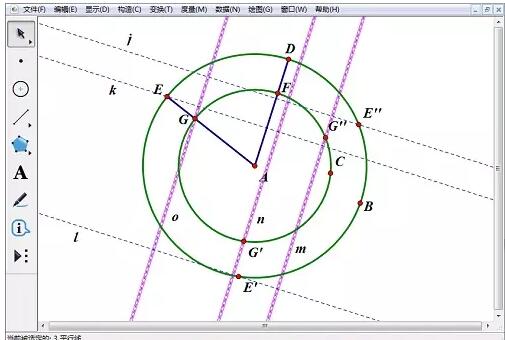
5. Dessinez l'intersection H des lignes droites j et m, l'intersection I de o et k, et l'intersection J de l et n. Sélectionnez les points I, J, H, sélectionnez [Construction] - [Segment de ligne. ] et convertissez la ligne. Le type est défini sur [ligne continue]. Masquez les trois droites perpendiculaires et les trois droites parallèles, ainsi que les points G, G’, G’’, E’ et E’’.

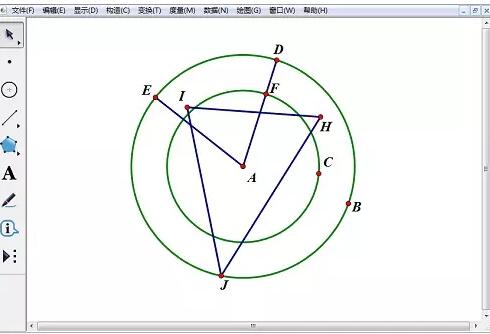
6. Sélectionnez le point A et le segment de ligne AD, sélectionnez la commande [Construction]-[Ligne perpendiculaire] et choisissez n'importe quel point O sur cette ligne verticale. Cachez ensuite cette ligne. Utilisez l'outil Segment de ligne pour tracer des segments de ligne OH, OI, OJ et OA, où OA est une ligne pointillée.

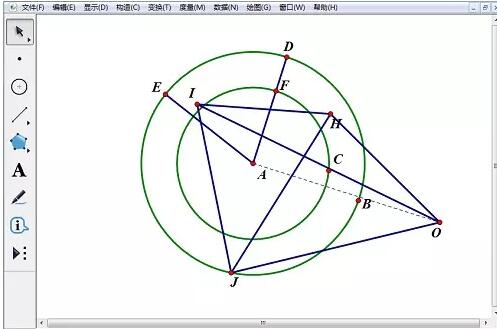
7. Sélectionnez le point E, sélectionnez la commande [Modifier]-[Bouton d'opération]-[Animation], réglez la direction sur [Antihoraire], la vitesse sur [Vitesse moyenne] et changez l'étiquette du bouton sur [Rotation] . Masquez simplement le segment de droite AD, le segment de droite AE, le point D, le point E, le point C, le point B et le grand cercle.

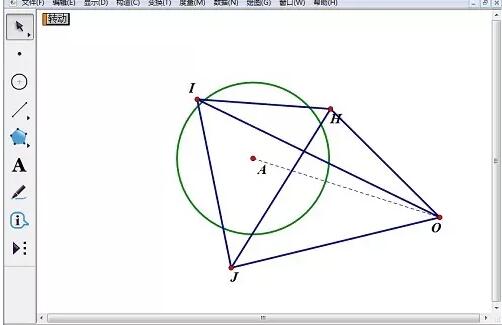
Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!