
Le MLP (Multilayer Perceptron) est utilisé depuis des décennies. N'y a-t-il vraiment pas d'autre choix ?
Multilayer Perceptron (MLP), également connu sous le nom de feedforward entièrement connecté Neural Network, est l'élément fondamental des modèles d'apprentissage profond d'aujourd'hui.
L'importance des MLP ne peut être surestimée car ils constituent la méthode par défaut pour approximer les fonctions non linéaires dans l'apprentissage automatique.
Cependant, MLP est-il le meilleur régresseur non linéaire que nous puissions construire ? Bien que les MLP soient largement utilisés, ils présentent des inconvénients importants. Par exemple, dans les modèles Transformer, les MLP consomment presque tous les paramètres non intégrés et sont généralement moins interprétables par rapport aux couches d'attention sans outils d'analyse de post-traitement.
Alors, existe-t-il une alternative au MLP ?
Aujourd'hui, KAN est apparu.

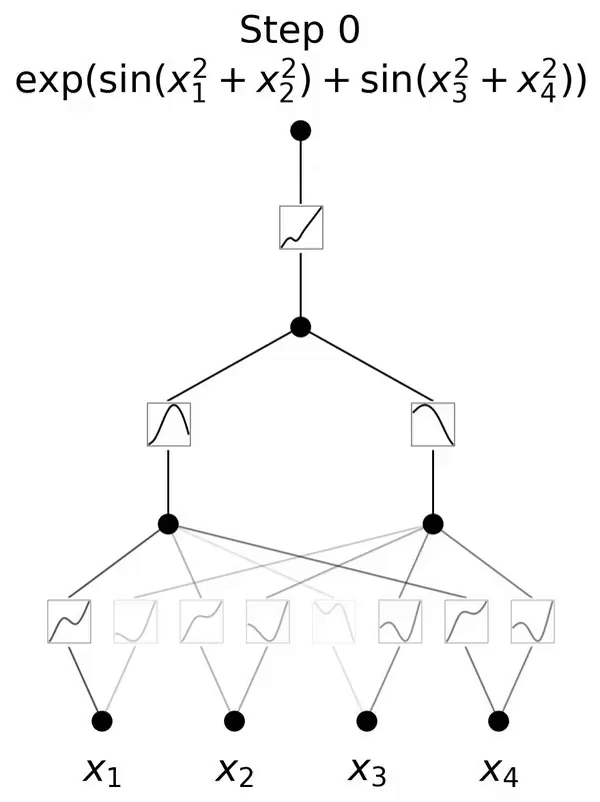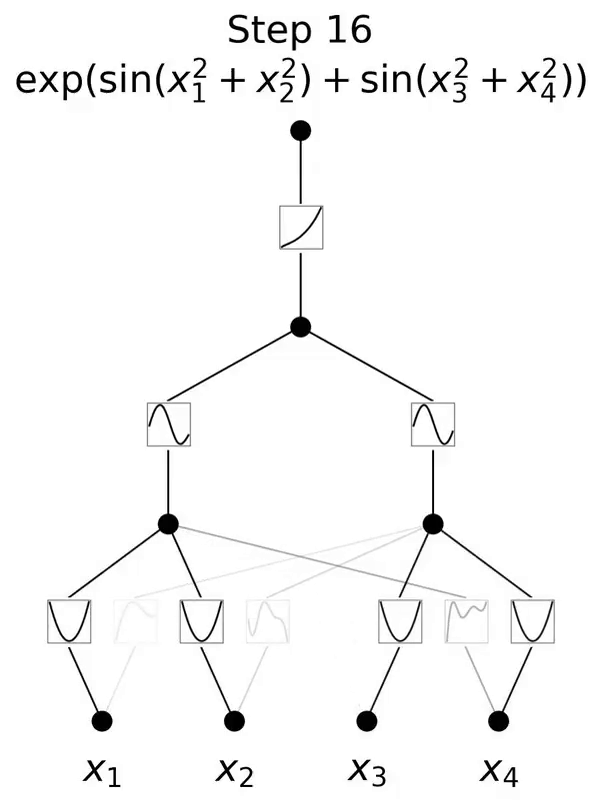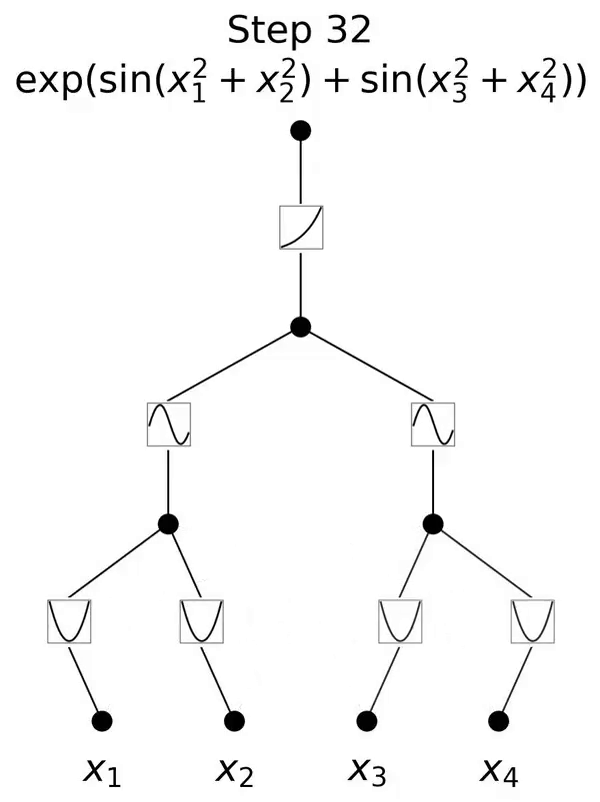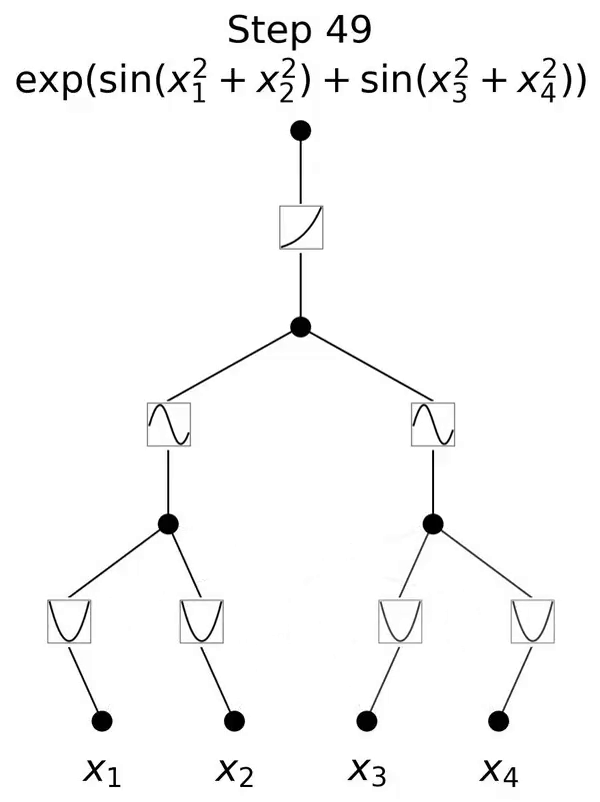

Il s'agit d'un réseau inspiré du théorème de représentation de Kolmogorov-Arnold.
Lien : https://arxiv.org/pdf/2404.19756
Github : https://github.com/KindXiaoming/pykan
Dès la publication de l'étude, elle a fait sensation sur les plateformes sociales étrangères, une attention et des discussions approfondies.
Certains internautes ont déclaré que Kolmogorov avait découvert le réseau neuronal multicouche dès 1957, bien avant l'article de Rumerhart, Hinton et William de 1986, mais il a été ignoré par l'Occident.

Certains internautes ont également déclaré que la publication de cet article signifie que le glas du deep learning a sonné.

Certains internautes se demandaient si cette recherche serait aussi perturbatrice que l'article Transformer.

Mais certains auteurs ont déclaré avoir fait la même chose en s'appuyant sur la technique améliorée de Kolmogrov-Gabor en 2018-19.
Ensuite, regardons de quoi parle cet article ?
Présentation de l'article
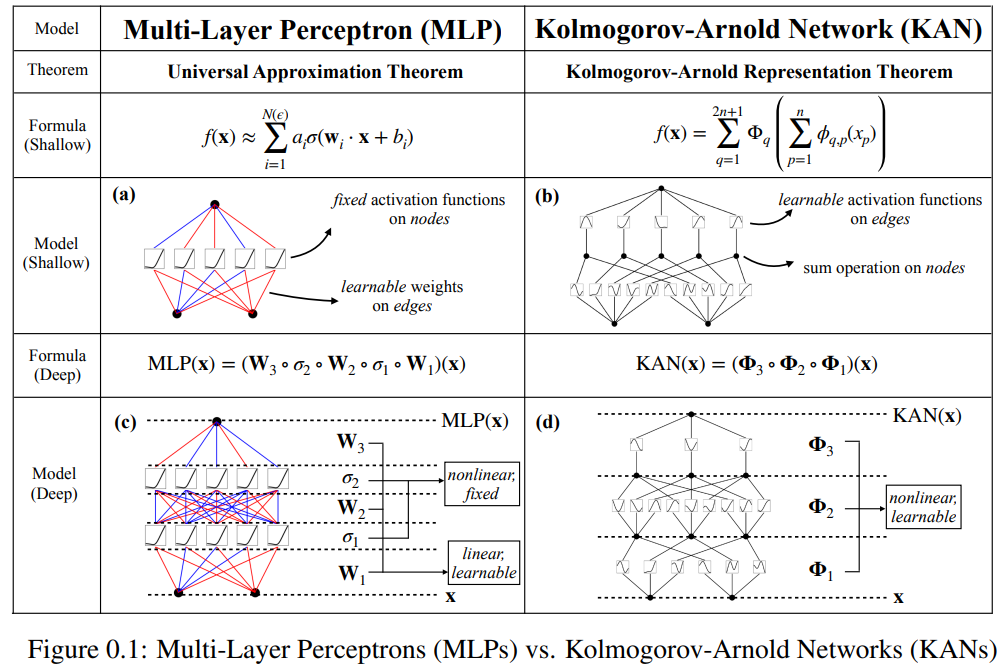
Cet article propose une alternative prometteuse aux perceptrons multicouches (MLP) appelée réseaux de Kolmogorov-Arnold (KAN). La conception de MLP s'inspire du théorème d'approximation universelle, tandis que la conception de KAN s'inspire du théorème de représentation de Kolmogorov-Arnold. Semblable au MLP, KAN a une structure entièrement connectée. Alors que MLP place des fonctions d'activation fixes sur les nœuds (neurones), KAN place des fonctions d'activation apprenables sur les bords (poids), comme le montre la figure 0.1. Par conséquent, KAN n’a aucune matrice de poids linéaire : chaque paramètre de poids est remplacé par une fonction unidimensionnelle apprenable paramétrée comme une spline. Les nœuds de KAN additionnent simplement les signaux entrants sans appliquer aucune transformation non linéaire.
Certaines personnes peuvent craindre que le coût de KAN soit trop élevé car les paramètres de poids de chaque MLP deviennent la fonction spline de KAN. Cependant, KAN permet un graphe de calcul beaucoup plus petit que MLP. Par exemple, les chercheurs ont démontré une solution PED : un KAN à deux couches d'une largeur de 10 est 100 fois plus précis qu'un MLP à quatre couches d'une largeur de 100 (les MSE sont respectivement de 10^-7 et 10^-5), et est également meilleur en termes d'efficacité des paramètres Amélioré de 100 fois (le nombre de paramètres est respectivement de 10 ^ 2 et 10 ^ 4).
La possibilité d'utiliser le théorème de représentation de Kolmogorov-Arnold pour construire des réseaux de neurones a été étudiée. Cependant, la plupart des travaux restent bloqués sur la représentation originale de profondeur 2 et de largeur (2n + 1), et il n'y a aucune possibilité d'exploiter des techniques plus modernes (par exemple, la rétropropagation) pour entraîner le réseau. La contribution de cet article est de généraliser la représentation originale de Kolmogorov-Arnold à une largeur et une profondeur arbitraires, la rendant ainsi revitalisée dans le domaine actuel de l'apprentissage profond, tout en utilisant un grand nombre d'expériences empiriques pour mettre en évidence son rôle potentiel en tant que modèle de base de « IA + science", qui bénéficie de la précision et de l'interprétabilité de KAN.
Bien que KAN ait de bonnes capacités d'explication mathématique, il ne s'agit en fait que d'une combinaison de splines et de MLP, profitant des avantages des deux et évitant les inconvénients. Les splines sont très précises sur les fonctions de faible dimension, faciles à ajuster localement et peuvent basculer entre différentes résolutions. Cependant, comme les splines ne peuvent pas exploiter les structures combinatoires, elles souffrent de graves problèmes de COD. Les MLP, en revanche, sont moins affectés par COD en raison de leurs capacités d'apprentissage de fonctionnalités, mais ne sont pas aussi précis que les splines dans les espaces de faible dimension car ils ne peuvent pas optimiser les fonctions univariées.
Afin d'apprendre avec précision une fonction, le modèle doit non seulement apprendre la structure combinatoire (degrés de liberté externes), mais également bien se rapprocher de la fonction univariée (degrés de liberté internes). Les KAN sont de tels modèles car ils ressemblent aux MLP en externe et aux splines en interne. En conséquence, KAN peut non seulement apprendre des fonctionnalités (grâce à leur similarité externe avec les MLP), mais également optimiser ces fonctionnalités apprises avec une très grande précision (grâce à leur similarité interne avec les splines).
Par exemple, pour une fonction de grande dimension :
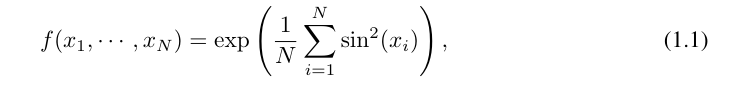
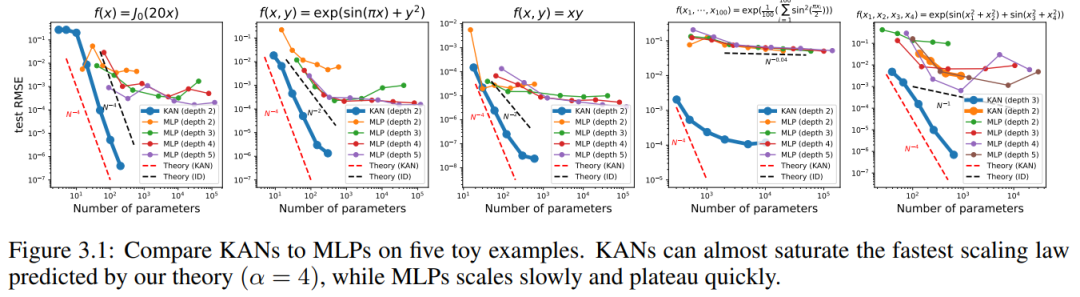
Lorsque N est grand, la spline échouera à cause de COD bien qu'il soit possible pour MLP d'apprendre une structure additive généralisée, il utilise, par exemple, un ; La fonction d'activation ReLU pour se rapprocher des fonctions exponentielles et sinusoïdales est très inefficace. En revanche, KAN est capable d’apprendre très bien les structures combinatoires et les fonctions univariées, surpassant ainsi largement MLP (voir Figure 3.1).
Dans cet article, les chercheurs montrent un grand nombre de valeurs expérimentales, qui reflètent l'amélioration significative de KAN dans le MLP en termes de précision et d'interprétabilité. La structure du document est présentée dans la figure 2.1 ci-dessous. Le code est disponible sur https://github.com/KindXiaoming/pykan et peut également être installé via pip install pykan.
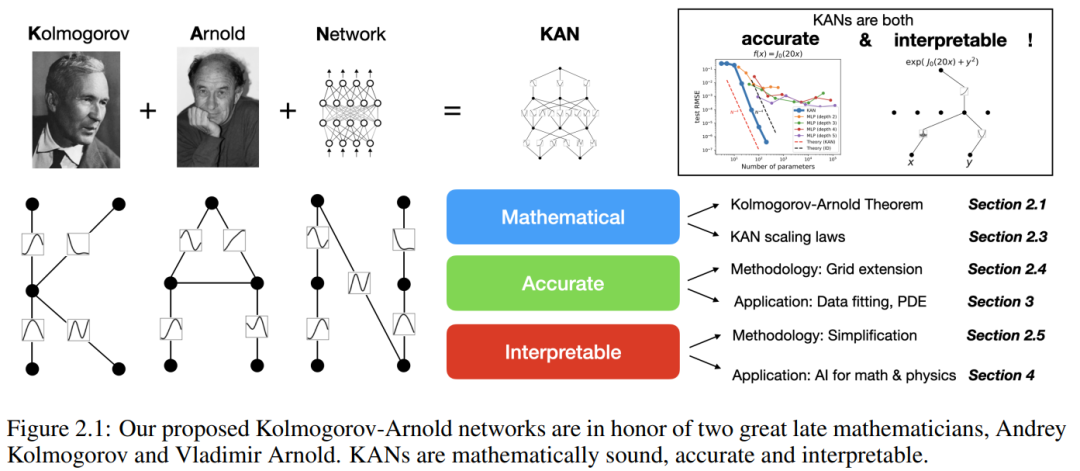
Réseau de Kolmogorov-Arnold (KAN)
Théorème de représentation de Kolmogorov-Arnold
Vladimir Arnold et Andrey Kolmogorov ont prouvé que si f est une fonction continue multivariable sur un domaine borné, alors f peut s'écrire comme une combinaison finie d'une fonction continue à variable unique et d'opérations d'addition binaires. Plus précisément, pour une fonction lisse f : [0, 1]^n → R, elle peut être exprimée comme :
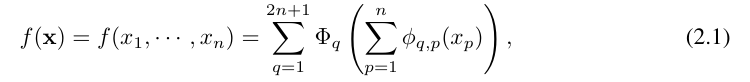 où
où 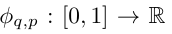 et
et 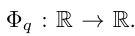
Dans un sens, elles présentent la seule vraie multivariée. La fonction est additive car toutes d'autres fonctions peuvent être représentées par des fonctions et des sommations à variable unique. On pourrait penser que c’est une bonne nouvelle pour l’apprentissage automatique : apprendre une fonction de grande dimension revient à apprendre une fonction unidimensionnelle en quantités polynomiales. Cependant, ces fonctions unidimensionnelles peuvent être non lisses, voire fractales, et ne peuvent donc pas être apprises en pratique. Le théorème de représentation de Kolmogorov-Arnold constitue donc essentiellement une condamnation à mort en apprentissage automatique, considéré comme théoriquement correct mais pratiquement inutile.
Cependant, les chercheurs sont plus optimistes quant à la faisabilité du théorème de Kolmogorov-Arnold dans l'apprentissage automatique. Premièrement, il n’est pas nécessaire de s’en tenir à l’équation originale, qui ne comporte que deux couches de non-linéarité et un petit nombre de termes (2n + 1) dans une couche cachée : le chercheur généralisera le réseau à des largeurs et profondeurs arbitraires. Deuxièmement, la plupart des fonctions dans la science et dans la vie quotidienne sont généralement fluides et ont des structures combinatoires clairsemées, ce qui peut faciliter des représentations fluides de Kolmogorov-Arnold.
KAN Architecture
Supposons qu'il existe une tâche d'apprentissage supervisé composée de paires d'entrées et de sorties {x_i, y_i}, et que le chercheur espère trouver une fonction f telle que y_i ≈ f (x_i) pour tous les points de données. L'équation (2.1) signifie que si les fonctions à variable unique appropriées 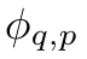 et
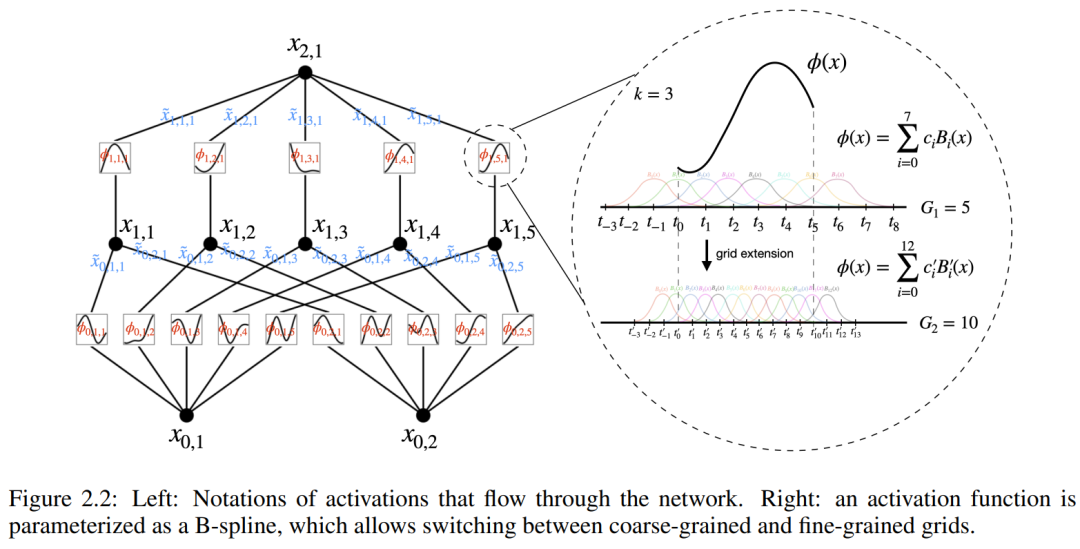
et 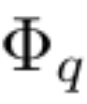 peuvent être trouvées, alors la tâche est accomplie. Cela incite les chercheurs à concevoir un réseau neuronal qui paramétrise explicitement l’équation (2.1). Puisque toutes les fonctions à apprendre sont des fonctions univariées, le chercheur paramétre chaque fonction unidimensionnelle comme une courbe B-spline avec des coefficients apprenables de fonctions de base B-spline locales (voir le côté droit de la figure 2.2). Nous avons maintenant un prototype de KAN, dont le graphe de calcul est entièrement spécifié par l'équation (2.1) et illustré dans la figure 0.1(b) (dimension d'entrée n = 2), qui ressemble à un réseau neuronal à deux couches avec des fonctions d'activation placées sur arêtes au lieu de nœuds (une simple sommation est effectuée sur les nœuds) et la largeur de la couche intermédiaire est de 2n + 1.
peuvent être trouvées, alors la tâche est accomplie. Cela incite les chercheurs à concevoir un réseau neuronal qui paramétrise explicitement l’équation (2.1). Puisque toutes les fonctions à apprendre sont des fonctions univariées, le chercheur paramétre chaque fonction unidimensionnelle comme une courbe B-spline avec des coefficients apprenables de fonctions de base B-spline locales (voir le côté droit de la figure 2.2). Nous avons maintenant un prototype de KAN, dont le graphe de calcul est entièrement spécifié par l'équation (2.1) et illustré dans la figure 0.1(b) (dimension d'entrée n = 2), qui ressemble à un réseau neuronal à deux couches avec des fonctions d'activation placées sur arêtes au lieu de nœuds (une simple sommation est effectuée sur les nœuds) et la largeur de la couche intermédiaire est de 2n + 1.
Comme mentionné précédemment, dans la pratique, de tels réseaux sont considérés comme trop simples pour approximer n'importe quelle fonction avec des splines de lissage avec une précision arbitraire. Par conséquent, les chercheurs généralisent KAN à des réseaux plus larges et plus profonds. Puisque la représentation de Kolmogorov-Arnold correspond à un KAN à deux couches, il n’est pas clair comment approfondir le KAN.
Le point marquant est que les chercheurs ont remarqué l’analogie entre MLP et KAN. Dans MLP, une fois qu'une couche (constituée de transformations linéaires et de non-linéarités) est définie, plusieurs couches peuvent être empilées pour approfondir le réseau. Pour construire un KAN profond, vous devez d'abord répondre : « Qu'est-ce qu'une couche KAN ? » Les chercheurs ont découvert qu'une couche KAN avec une entrée n_in-dimensionnelle et une sortie n_out-dimensionnelle peut être définie comme une matrice de fonctions unidimensionnelle.
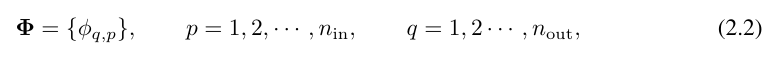
where fonction  a des paramètres entraînables comme décrit ci-dessous. Dans le théorème de Kolmogorov-Arnold, les fonctions internes forment une couche KAN avec n_in = n et n_out = 2n+1, et les fonctions externes forment une couche KAN avec n_in = 2n + 1 et n_out = 1. Par conséquent, la représentation de Kolmogorov-Arnold dans l’équation (2.1) est simplement une combinaison de deux couches KAN. Désormais, avoir une représentation Kolmogorov-Arnold plus profonde signifie : il suffit d'empiler plus de couches KAN !
a des paramètres entraînables comme décrit ci-dessous. Dans le théorème de Kolmogorov-Arnold, les fonctions internes forment une couche KAN avec n_in = n et n_out = 2n+1, et les fonctions externes forment une couche KAN avec n_in = 2n + 1 et n_out = 1. Par conséquent, la représentation de Kolmogorov-Arnold dans l’équation (2.1) est simplement une combinaison de deux couches KAN. Désormais, avoir une représentation Kolmogorov-Arnold plus profonde signifie : il suffit d'empiler plus de couches KAN !
Une compréhension plus approfondie nécessite l'introduction de certains symboles. Vous pouvez vous référer à la figure 2.2 (à gauche) pour des exemples spécifiques et une compréhension intuitive. La forme de KAN est représentée par un tableau d'entiers :

où n_i est le nombre de nœuds dans la i-ème couche du graphe informatique. Ici, (l, i) représente le i-ème neurone de la l-ème couche, et x_l,i représente la valeur d'activation du neurone (l, i). Entre la lème couche et la l + 1ème couche, il y a n_l*n_l+1 fonctions d'activation : la fonction d'activation reliant (l, j) et (l + 1, i) s'exprime par

fonction ϕ_l, La la valeur de pré-activation de i,j est simplement exprimée par x_l,i ; la valeur de post-activation de ϕ_l,i,j est 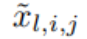 ≡ ϕ_l,i,j (x_l,i). La valeur d'activation du (l + 1, j)ème neurone est la somme de toutes les valeurs d'activation entrantes :
≡ ϕ_l,i,j (x_l,i). La valeur d'activation du (l + 1, j)ème neurone est la somme de toutes les valeurs d'activation entrantes :
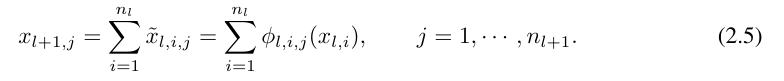
exprimée sous forme matricielle comme suit :

où, Φ_l est la couche KAN correspondant au Matrice de fonctions de la lième couche. Un réseau KAN général est une combinaison de L couches : étant donné un vecteur d'entrée x_0 ∈ R^n0, la sortie de KAN est
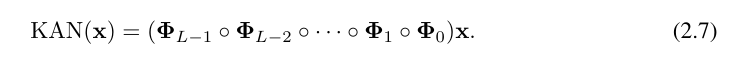
L'équation ci-dessus peut également être écrite dans une situation similaire à l'équation (2.1), en supposant que la dimension de sortie n_L = 1, et définissons f (x) ≡ KAN (x) :
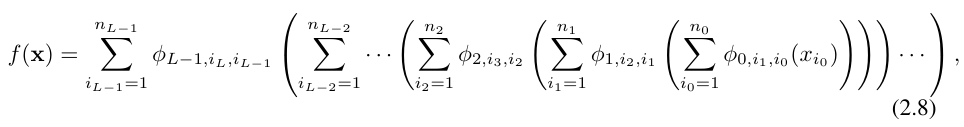
Écrire ainsi est assez fastidieux. En revanche, l’abstraction de la couche KAN par les chercheurs et sa visualisation sont plus concises et intuitives. La représentation originale de Kolmogorov-Arnold (2.1) correspond à un KAN à 2 couches de forme [n, 2n + 1, 1]. Notez que toutes les opérations sont différenciables, donc KAN peut être formé avec rétropropagation. À titre de comparaison, MLP peut s'écrire comme l'entrelacement de la transformation affine W et de σ non linéaire :
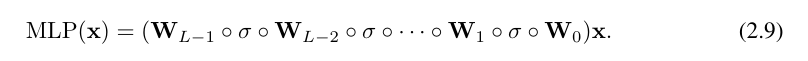
Évidemment, MLP traite les transformations linéaires et les non-linéarités respectivement comme W et σ, tandis que KAN les traite ensemble comme Φ. Dans les figures 0.1 (c) et (d), les chercheurs montrent le MLP à trois couches et le KAN à trois couches pour illustrer la différence entre eux.
Précision de KAN
Dans l'article, les auteurs ont également démontré que KAN est plus efficace que MLP pour représenter des fonctions dans diverses tâches (régression et résolution d'équations aux dérivées partielles). Et ils montrent aussi que KAN peut fonctionner naturellement en apprentissage continu sans oubli catastrophique.
Ensemble de données de jouets
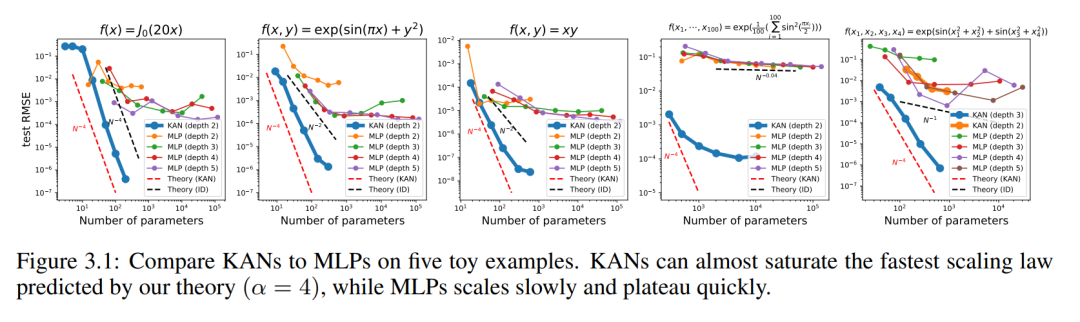
Nous traçons le test RMSE de KAN et MLP en fonction du nombre de paramètres dans la figure 3.1, démontrant que KAN a de meilleures courbes d'échelle que MLP, en particulier dans les exemples de grande dimension. À titre de comparaison, les auteurs tracent la droite prédite selon leur théorie KAN, sous la forme de la ligne pointillée rouge (α = k + 1 = 4), et la droite prédite selon Sharma & Kaplan [17], sous la forme de la ligne pointillée noire (α = (k + 1 )/ré = 4/ré). KAN peut presque remplir la ligne rouge la plus raide, tandis que MLP a même du mal à converger au rythme de la ligne noire, plus lente, et atteint rapidement un plateau. Les auteurs notent également que pour le dernier exemple, le KAN à 2 couches est bien moins performant que le KAN à 3 couches (forme [4, 2, 2, 1]). Cela met en évidence que les KAN plus profonds sont plus expressifs, et il en va de même pour les MLP : les MLP plus profonds sont plus expressifs que les MLP moins profonds.
Fonctions spéciales
Nous montrons les deux points suivants dans cette section :
(1) Il est possible de trouver (approximativement) des représentations KA compactes de fonctions spéciales, ce qui est révélé du point de vue de Kolmogorov- Représentation d'Arnold Nouvelles propriétés mathématiques des fonctions spéciales.
(2) KAN est plus efficace et précis que MLP pour représenter les fonctions spéciales.
Pour chaque ensemble de données et chaque famille de modèles (KAN ou MLP), les auteurs ont tracé la frontière de Pareto sur le nombre de paramètres et le plan RMSE, comme le montre la figure 3.2.
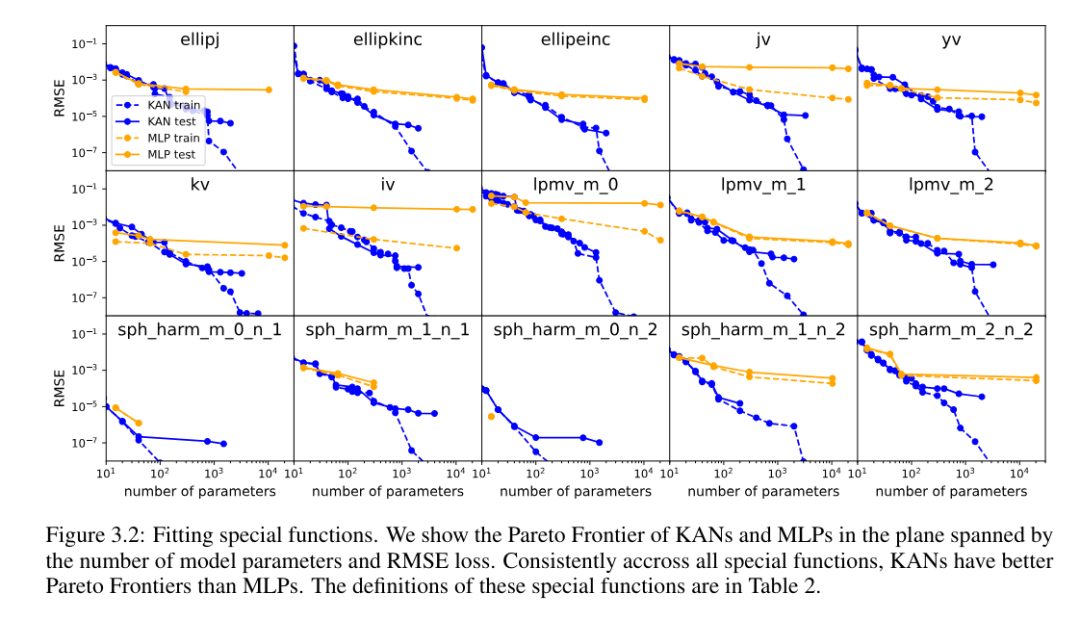
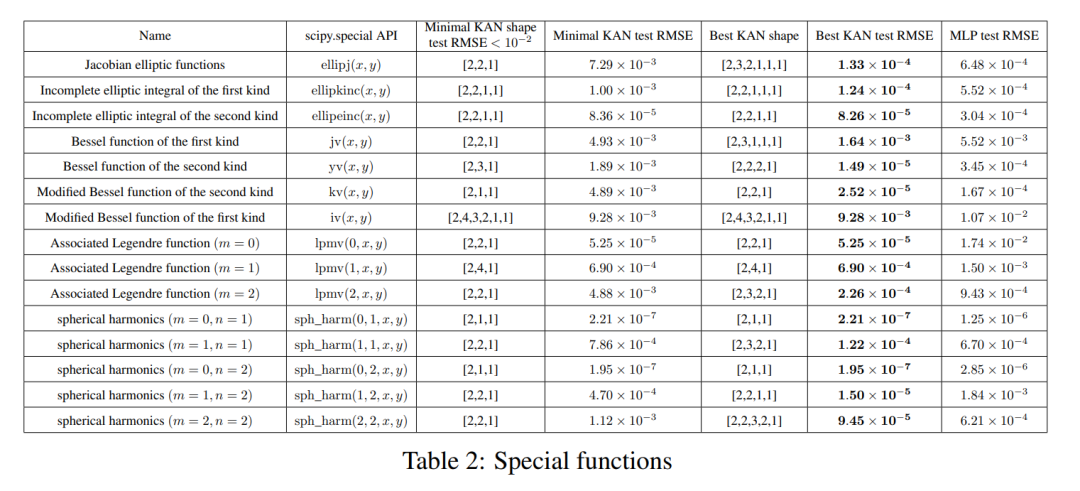
KAN fonctionne systématiquement mieux que MLP, c'est-à-dire qu'avec le même nombre de paramètres, KAN est capable d'obtenir des pertes d'entraînement/test inférieures à celles de MLP. De plus, les auteurs rapportent dans le tableau 2 la forme (étonnamment compacte) du KAN pour la fonction spéciale qu'ils ont automatiquement découverte. D’une part, il est intéressant d’expliquer mathématiquement le sens de ces représentations compactes. D'un autre côté, ces représentations compactes signifient qu'il est possible de décomposer une table de recherche de grande dimension en plusieurs tables de recherche unidimensionnelles, ce qui peut potentiellement économiser beaucoup de mémoire au détriment de l'exécution de certaines opérations d'addition au moment de l'inférence (presque négligeable) .
Feynman Dataset
Le paramètre de la section précédente est que nous connaissons clairement la "vraie" forme KAN. La configuration de la section précédente est que nous ne connaissons évidemment pas la « vraie » forme KAN. Cette section étudie un cadre intermédiaire : étant donné la structure de l'ensemble de données, nous pourrions construire des KAN à la main, mais nous ne sommes pas sûrs qu'ils soient optimaux.
Pour chaque combinaison d'hyperparamètres, l'auteur a essayé 3 graines aléatoires. Pour chaque ensemble de données (équation) et chaque méthode, ils rapportent dans le tableau 3 les résultats du meilleur modèle (forme KAN minimale ou perte de test la plus faible) à des graines et à des profondeurs aléatoires.
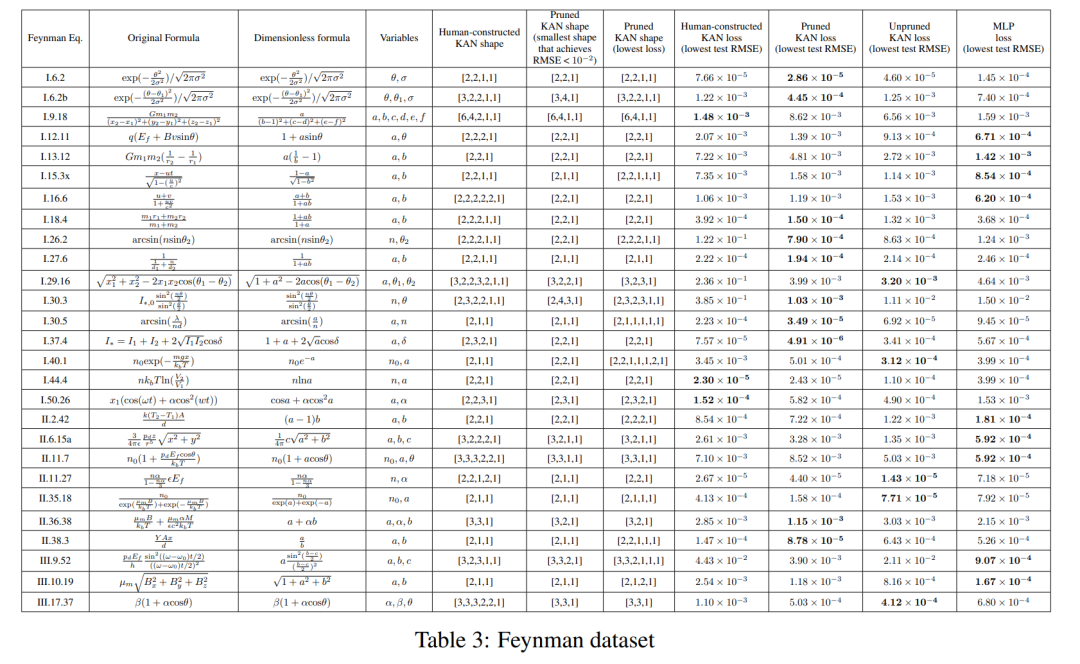
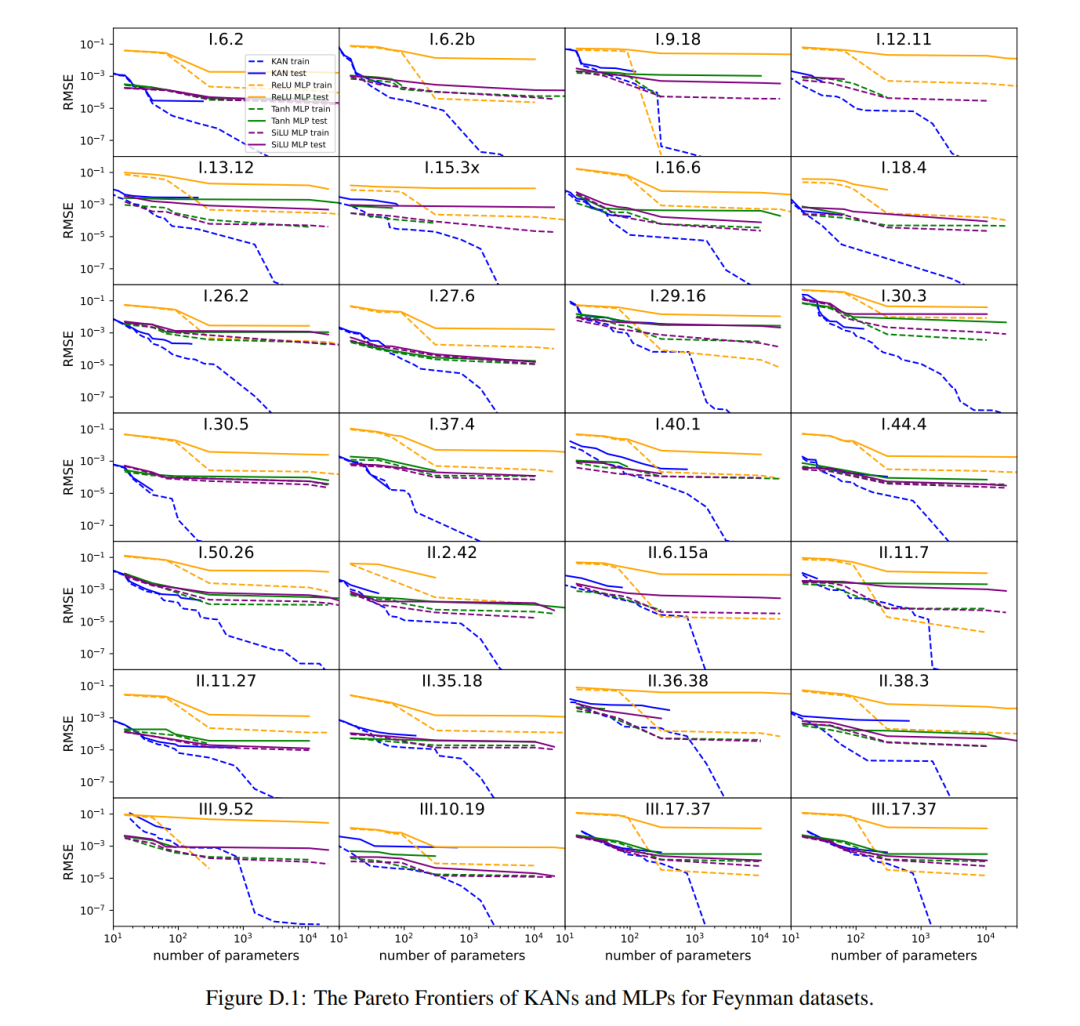
Ils ont constaté que MLP et KAN fonctionnaient aussi bien en moyenne. Pour chaque jeu de données et chaque famille de modèles (KAN ou MLP), les auteurs ont tracé la frontière de Pareto sur le plan formé par le nombre de paramètres et la perte RMSE, comme le montre la figure D.1. Ils spéculent que l'ensemble de données de Feynman est trop simple pour permettre des améliorations supplémentaires par KAN, dans le sens où les dépendances variables sont souvent lisses ou monotones, contrairement à la complexité des fonctions spéciales, qui présentent souvent un comportement oscillatoire.
Résoudre des équations aux dérivées partielles
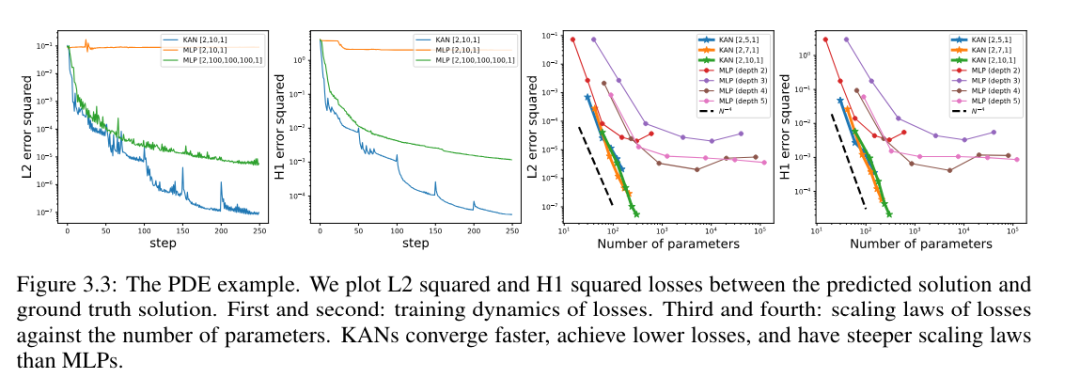
L'auteur a comparé les architectures KAN et MLP en utilisant les mêmes hyperparamètres. Ils ont mesuré l'erreur dans la norme L^2 et la norme d'énergie (H^1), et ont observé que KAN obtenait une meilleure loi d'échelle et une erreur plus petite tout en utilisant un réseau plus petit et moins de paramètres, voir Figure 3.3. Par conséquent, ils ont émis l’hypothèse que KAN pourrait potentiellement servir de bonne représentation de réseau neuronal pour la réduction du modèle d’équation aux dérivées partielles (PDE).
Apprentissage continu
Les auteurs montrent que KAN a une plasticité locale et peut éviter un oubli catastrophique en exploitant la localité des splines. L'idée est simple : puisque la base de la spline est locale, un échantillon n'affectera que quelques coefficients de spline proches, tout en laissant les coefficients distants inchangés (c'est ce que nous voulons, puisque les régions distantes peuvent déjà stocker les coefficients dont nous voulons retenir les informations) . En revanche, étant donné que MLP utilise généralement des fonctions d'activation globales telles que ReLU/Tanh/SiLU, etc., tout changement local peut se propager de manière incontrôlable vers des régions distantes, détruisant les informations qui y sont stockées.
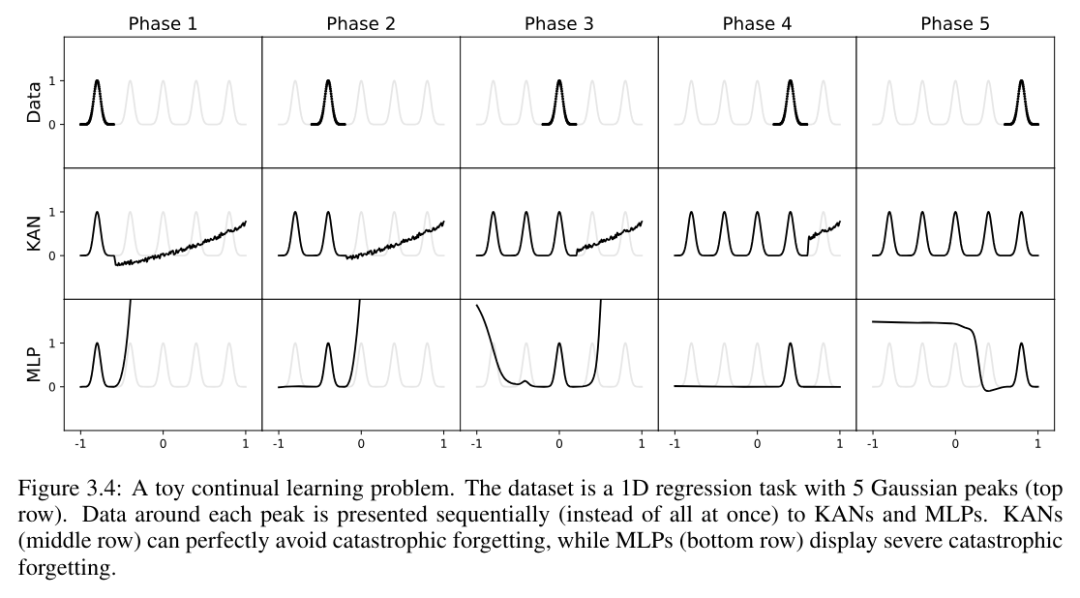
L'auteur utilise un exemple simple pour vérifier cette intuition. Une tâche de régression unidimensionnelle se compose de 5 pics gaussiens. Les données autour de chaque pic sont présentées séquentiellement (plutôt que toutes en même temps), comme le montre la rangée supérieure de la figure 3.4, présentée séparément au KAN et au MLP. Les résultats de prédiction de KAN et MLP après chaque étape d'entraînement sont affichés respectivement dans les rangées du milieu et du bas. Comme prévu, KAN reconstruit uniquement les régions où les données existent au stade actuel, laissant les régions précédentes inchangées. En revanche, MLP reconstruit la région entière après avoir vu un nouvel échantillon de données, conduisant à un oubli catastrophique.
KAN est interprétable
Dans le chapitre 4 de l'article, les auteurs montrent que KAN est interprétable et interactif grâce aux techniques développées dans la section 2.5. Ils voulaient tester l'application du KAN non seulement sur des tâches de synthèse (sections 4.1 et 4.2), mais aussi dans des recherches scientifiques réelles. Ils montrent que les KAN sont capables de (re)découvrir des relations complexes dans la théorie des jonctions (Section 4.3) et des limites de transition de phase dans la physique de la matière condensée (Section 4.4). En raison de sa précision et de son interprétabilité, KAN a le potentiel de devenir un modèle fondamental pour l’IA + Science.
Discussion
Dans l'article, l'auteur discute des limites et des orientations de développement futures de KAN du point de vue des fondements mathématiques, des algorithmes et des applications.
Aspects mathématiques : Bien que l'auteur ait effectué une analyse mathématique préliminaire des KAN (Théorème 2.1), leur compréhension mathématique est encore très limitée. Le théorème de représentation de Kolmogorov-Arnold a été étudié mathématiquement en profondeur, mais il correspond à un KAN de forme [n, 2n + 1, 1], qui est une sous-classe très restreinte de KAN. Le succès empirique sur des KAN plus profonds implique-t-il quelque chose de mathématiquement fondamental ? Un théorème de Kolmogorov-Arnold généralisé attrayant pourrait définir des représentations de Kolmogorov-Arnold « plus profondes » au-delà de la combinaison de deux couches, et potentiellement relier la douceur de la fonction d'activation à la profondeur. Supposons qu'il existe des fonctions qui ne peuvent pas être représentées de manière fluide dans la représentation originale de Kolmogorov-Arnold (profondeur 2), mais qui peuvent être représentées de manière fluide à une profondeur de 3 ou plus. Peut-on utiliser ce concept de « profondeur Kolmogorov-Arnold » pour caractériser les classes de fonctions ?
Au niveau de l'algorithme, ils ont discuté des points suivants :
Précision. Il existe de nombreuses options en matière de conception d'architecture et de formation qui n'ont pas été entièrement étudiées. Il peut donc exister des alternatives pour améliorer encore la précision. Par exemple, la fonction d'activation spline peut être remplacée par des fonctions à base radiale ou d'autres fonctions de noyau locales. Des stratégies de grille adaptatives peuvent être utilisées.
Efficacité. L'une des principales raisons pour lesquelles KAN est lent est que différentes fonctions d'activation ne peuvent pas tirer parti du calcul par lots (de grandes quantités de données transitent par la même fonction). En fait, on peut interpoler entre MLP (toutes les fonctions d'activation sont les mêmes) et KAN (toutes les fonctions d'activation sont différentes) en regroupant les fonctions d'activation en groupes ("multiples"), où les membres du groupe partagent la même fonction d'activation.
Un mélange de KAN et MLP. Par rapport au MLP, KAN présente deux différences principales :
(i) La fonction d'activation est située sur les bords au lieu de nœuds ;
(ii) La fonction d'activation est apprenable au lieu d'être fixe ;
Quel changement explique le mieux les avantages du KAN ? Les auteurs présentent leurs résultats préliminaires en Annexe B, où ils étudient un modèle avec (ii), c'est à dire que la fonction d'activation est apprenable (comme KAN), mais sans (i), c'est à dire que la fonction d'activation est localisée aux nœuds (comme un MLP). ). De plus, on peut construire un autre modèle dont la fonction d'activation est fixe (comme MLP) mais située sur les bords (comme KAN).
Adaptabilité. En raison de la localisation inhérente des fonctions de base spline, nous pouvons introduire de l'adaptabilité dans la conception et la formation des KAN pour améliorer la précision et l'efficacité : voir [93, 94] pour des idées de formation multi-niveaux telles que les méthodes multigrilles ou les fonctions de base dépendantes du domaine. comme les méthodes multi-échelles dans [95].
Applications : Les auteurs ont présenté des preuves préliminaires selon lesquelles KAN est plus efficace que MLP dans les tâches liées à la science, telles que l'ajustement d'équations physiques et la résolution d'EDP. Ils prévoient que KAN pourrait également être prometteur dans la résolution des équations de Navier-Stokes, de la théorie fonctionnelle de la densité ou de toute autre tâche pouvant être formulée sous forme de solution de régression ou d'EDP. Ils espèrent également appliquer KAN à des tâches liées au machine learning, qui nécessiteront d'intégrer KAN dans les architectures actuelles, comme les transformateurs - on peut proposer des "kansformers" pour remplacer les MLP par KAN dans les transformateurs.
KAN comme modèles de langage pour l'IA + la science : les grands modèles de langage sont transformateurs car ils sont utiles à toute personne sachant utiliser le langage naturel. Le langage de la science est celui des fonctions. Les KAN sont composés de fonctions interprétables. Ainsi, lorsqu'un utilisateur humain regarde un KAN, c'est comme communiquer avec lui en utilisant un langage fonctionnel. Ce paragraphe vise à mettre l’accent sur le paradigme de collaboration IA-scientifique plutôt que sur l’outil spécifique KAN. Tout comme les gens utilisent différentes langues pour communiquer, les auteurs prévoient qu'à l'avenir, KAN ne sera qu'un des langages de l'IA + de la science, même si KAN sera l'un des premiers langages permettant à l'IA et aux humains de communiquer. communiquer. Cependant, grâce à KAN, le paradigme de collaboration entre scientifiques et IA n’a jamais été aussi simple et pratique, ce qui nous amène à repenser la façon dont nous voulons aborder l’IA et la science : voulons-nous des scientifiques en IA, ou voulons-nous une IA qui aide les scientifiques ? Une difficulté inhérente pour les scientifiques en IA (entièrement automatisée) est la difficulté de quantifier les préférences humaines, ce qui codifierait les préférences humaines en objectifs d’IA. En fait, les scientifiques de différents domaines peuvent avoir des sentiments différents quant aux fonctions qui sont simples ou explicables. Par conséquent, il est préférable que les scientifiques disposent d’une IA capable de parler le langage de la science (fonctions) et d’interagir facilement avec les préjugés inductifs de scientifiques individuels pour s’adapter à un domaine scientifique spécifique.
Question clé : KAN ou MLP ?
Actuellement, le plus gros goulot d'étranglement de KAN est sa lenteur d'entraînement. Avec le même nombre de paramètres, le temps de formation du KAN est généralement 10 fois supérieur à celui du MLP. Les auteurs déclarent que, pour être honnête, ils n'ont pas fait d'efforts pour optimiser l'efficacité de KAN, ils pensent donc que la lenteur de la formation de KAN est davantage un problème d'ingénierie qui peut être amélioré à l'avenir plutôt qu'une limitation fondamentale. Si quelqu'un souhaite former un modèle rapidement, il doit utiliser MLP. Cependant, dans d’autres cas, les KAN devraient être aussi bons, voire meilleurs, que les MLP, ce qui en vaut la peine. L'arbre de décision de la figure 6.1 peut aider à décider quand utiliser un KAN. En bref, si vous vous souciez de l'interprétabilité et/ou de la précision et que la lenteur de l'entraînement n'est pas un problème majeur, l'auteur recommande d'essayer KAN.
Pour plus de détails, veuillez lire l'article original.
Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!
 Construisez votre propre serveur git
Construisez votre propre serveur git
 La différence entre git et svn
La différence entre git et svn
 git annuler le commit soumis
git annuler le commit soumis
 Comment annuler l'erreur de commit git
Comment annuler l'erreur de commit git
 Comment comparer le contenu des fichiers de deux versions dans git
Comment comparer le contenu des fichiers de deux versions dans git
 Comment résoudre le problème d'occupation du port phpstudy
Comment résoudre le problème d'occupation du port phpstudy
 Comment redémarrer régulièrement
Comment redémarrer régulièrement
 qu'est-ce que xfce
qu'est-ce que xfce