Une brève discussion sur la mise en œuvre de huit tris majeurs dans les compétences javascript

Un mois après le début de l'année scolaire, j'ai rêvé à plusieurs reprises de questions sur l'algorithme de structure de données apparaissant dans les examens écrits. J'ai plus peur des structures de données que des "fantômes". Haha, il semble qu'il soit vraiment nécessaire de revoir les structures de données couramment utilisées pour éviter que le « cauchemar » ne se réalise.

Inutile de souligner l’importance des bases de la programmation telles que les structures de données, allons droit au but.

L'algorithme de tri est divisé en tri interne et tri externe. Le tri interne utilise la mémoire et seul le tri interne est abordé ici.

1. Tri par insertion : tri par insertion directe et tri Hill

2. Tri par sélection : tri par sélection simple et tri par tas

3. Tri par échange : tri à bulles et tri rapide

4, tri par fusion

5, tri par base

Tri par insertion directe

Idée de base : dans un ensemble de nombres à trier, en supposant que les nombres précédents (n-1) [n>=2] sont déjà dans l'ordre, insérez d'abord le n-ième nombre dans le nombre ordonné précédent, donc que ces n nombres sont également triés. Répétez ce cycle jusqu'à ce que tout soit en ordre.

Tri des collines

Idée de base : L'algorithme divise d'abord un ensemble de nombres à trier en plusieurs groupes selon un certain incrément d (n/2, n est le nombre à trier), et les indices enregistrés dans chaque groupe diffèrent de d . Effectuez un tri par insertion directe sur tous les éléments de chaque groupe, puis regroupez-les par un incrément plus petit (d/2) et effectuez un tri par insertion directe sur chaque groupe. Lorsque l'incrément est réduit à 1, le tri est terminé après le tri par insertion directe.

Tri par sélection simple

Idée de base : parmi un ensemble de nombres à trier, sélectionnez le plus petit nombre et échangez-le avec le nombre en première position, puis trouvez le plus petit nombre parmi les nombres restants et échangez-le avec le nombre en deuxième position. , alors Trouvez haha jusqu'à l'avant-dernier numéro et le dernier numéro.

Tri par tas

Idée de base : le tri par tas est un tri par sélection arborescente, qui constitue une amélioration efficace du tri par sélection directe.

Une séquence (h1, h2,...,hn) avec n éléments, si et seulement si (hi>=h2i,hi>=2i 1) ou (hi<=h2i,hi<=2i 1 ) ( i=1,2,...,n/2) est appelé un tas. Seuls les tas qui remplissent la première condition sont abordés ici. Il ressort de la définition d'un tas que l'élément supérieur du tas (c'est-à-dire le premier élément) doit être l'élément le plus grand (grand tas supérieur). Un arbre binaire complet peut représenter la structure d’un tas de manière très intuitive. Le sommet du tas est la racine, et les autres sont le sous-arbre gauche et le sous-arbre droit. Initialement, la séquence de nombres à trier est considérée comme un arbre binaire stocké séquentiellement, et leur ordre de stockage est ajusté pour qu'il devienne un tas. À ce stade, le nombre de nœuds racine du tas est le plus grand. Échangez ensuite le nœud racine avec le dernier nœud du tas. Réajustez ensuite les nombres précédents (n-1) pour former un tas. Et ainsi de suite, jusqu'à ce qu'il y ait un tas avec seulement deux nœuds, et qu'ils soient échangés, et finalement une séquence ordonnée de n nœuds est obtenue. D'après la description de l'algorithme, le tri du tas nécessite deux processus, l'un consiste à établir le tas et l'autre à échanger les positions entre le haut du tas et le dernier élément du tas. Le tri par tas se compose donc de deux fonctions. L'une est la fonction de pénétration pour construire le tas, et l'autre est la fonction permettant d'appeler à plusieurs reprises la fonction de pénétration pour implémenter le tri.

Tri à bulles

Idée de base : Dans un ensemble de nombres à trier, comparer et ajuster les deux nombres adjacents en séquence de haut en bas pour tous les nombres de la plage qui n'ont pas encore été triés, afin que le plus grand Les quelques coulent, et les plus petits montent. Autrement dit : chaque fois que deux nombres adjacents sont comparés et qu'il s'avère que leur ordre est opposé à l'exigence d'ordre, ils sont échangés.

Tri rapide

Idée de base : sélectionnez un élément de référence, généralement le premier élément ou le dernier élément, et divisez la séquence à trier en deux parties en une seule analyse, une partie est plus petite que l'élément de référence et l'autre partie est supérieure à ou égal à l'élément de référence. À ce stade, les éléments de référence sont dans leurs positions triées correctes, puis les deux parties divisées sont triées récursivement de la même manière.

Tri par fusion

Tri de base : la méthode de tri par fusion consiste à fusionner deux (ou plus) listes ordonnées en une nouvelle liste ordonnée, c'est-à-dire que la séquence à trier est divisée en plusieurs sous-séquences, chaque sous-séquence a une séquence. Fusionnez ensuite les sous-séquences ordonnées dans la séquence ordonnée globale.

Tri Radix

Idée de base : Unifiez toutes les valeurs à comparer (entiers positifs) avec la même longueur de chiffres, et ajoutez des zéros devant les nombres avec des chiffres plus courts. Ensuite, en commençant par le bit le plus bas, triez-les un par un. De cette manière, après tri du bit le plus faible au bit le plus élevé, la séquence devient une séquence ordonnée.

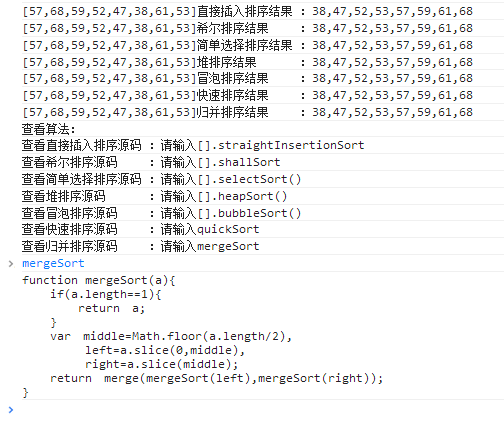
Adresse de démonstration du code : http://lovermap.sinaapp.com/test/sort.html

Nous analysons maintenant la stabilité de 8 algorithmes de tri.

(Il est demandé aux internautes de comprendre la stabilité du tri en combinant les idées de base du tri précédemment (les idées de base des 8 types de tri ont déjà été évoquées et ne seront pas répétées ici) sinon cela risque d'être un peu vague)

(1) Tri par insertion directe : Dans le tri par insertion générale, la comparaison part du dernier élément de la séquence ordonnée S'il est plus grand que lui, il est inséré directement derrière lui, sinon il reste. comparer en avant. Si un élément égal à l'élément inséré est trouvé, il est inséré après l'élément égal. Le tri par insertion est stable.

(2) Tri Hill : Le tri Hill est un tri par insertion d'éléments selon différentes longueurs de synchronisation. Un tri par insertion est stable et ne changera pas l'ordre relatif des mêmes éléments, mais dans des périodes différentes. le processus de tri par insertion, les mêmes éléments peuvent se déplacer dans leur tri par insertion respectif et la stabilité sera détruite, le tri Hill est donc instable.

(3) Tri par sélection simple : Dans une sélection, si l'élément actuel est plus petit qu'un élément et que le petit élément apparaît derrière un élément égal à l'élément actuel, alors il sera stable après échange Le sexe est détruit. C'est peut-être un peu vague rien que de le dire, regardons un petit exemple : 858410, lors du premier scan, le premier élément 8 sera échangé avec 4, alors l'ordre relatif des deux 8 dans la séquence originale est incohérent avec la séquence originale, donc le tri de sélection n'est pas possible Stabiliser.

(4) Tri des tas : Le processus de tri des tas consiste à sélectionner le plus grand (grand tas supérieur) ou le plus petit (petit tas supérieur) à partir du n/2ème et de ses nœuds enfants avec un total de 3 valeurs. Ce choix entre 3 éléments ne détruit certainement pas la stabilité. Mais lors de la sélection d'éléments pour les nœuds parents n/2-1, n/2-2, ..., il est possible que le n/2ème nœud parent échange l'élément suivant, et le n/2-1ème Le nœud parent ne le fait pas. échangez le même élément à la fin, donc le tri des tas n'est pas stable.

(5) Tri à bulles : Comme le montre le contenu précédent, le tri à bulles est une comparaison de deux éléments adjacents, et un échange se produit également entre ces deux éléments si les deux éléments sont égaux. pas besoin d'échanger. Le tri à bulles est donc stable.

(6) Tri rapide : Lorsque l'élément central est échangé avec un élément de la séquence, cela risque très probablement de perturber la stabilité de l'élément précédent. Regardons un petit exemple : 6 4 4 5 4 7 8 9. Lors de la première passe de tri, l'échange de l'élément central 6 et du troisième 4 détruira la séquence originale de l'élément 4, donc le tri rapide est instable.

(7) Tri par fusion : Dans la sous-colonne décomposée, lorsqu'il y a 1 ou 2 éléments, 1 élément ne sera pas échangé, et 2 éléments ne seront pas échangés s'ils sont de taille égale . Lors du processus de fusion de séquences, si les deux éléments actuels sont égaux, nous sauvegardons les éléments de la séquence précédente devant la séquence résultat, afin que le tri par fusion soit également stable.

(8) Tri par base : trier d'abord par ordre faible, puis collecter ; puis trier par ordre élevé, puis collecter et ainsi de suite, jusqu'à l'ordre le plus élevé ; Parfois, certains attributs ont un ordre de priorité. Ils sont d'abord triés par priorité faible, puis par priorité élevée. L'ordre final est que ceux ayant une priorité élevée viennent en premier, et ceux ayant la même priorité élevée et faible viennent en premier. Le tri Radix est basé sur un tri séparé et une collecte séparée, il est donc stable.

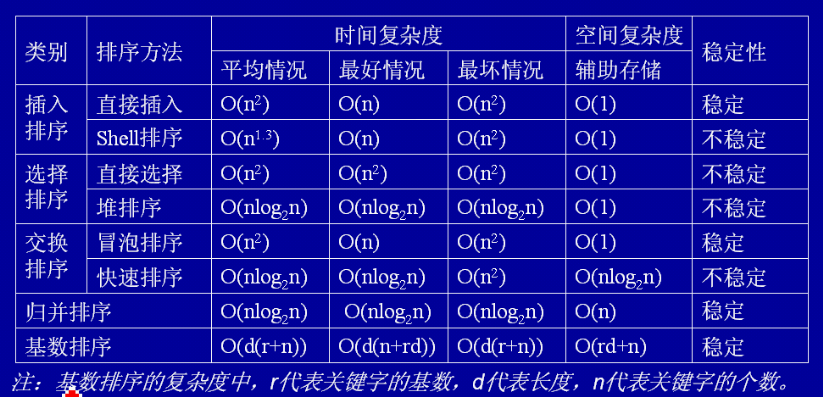
Résumé de la classification, de la stabilité, de la complexité temporelle et de la complexité spatiale de 8 types de tri :