Les performances des petits modèles sont saturées et les performances sont médiocres. La cause première est Softmax ?

L'émergence de petits modèles de langage vise à compenser les inconvénients d'une formation coûteuse et de l'inférence de grands modèles de langage, mais elle a aussi le fait que ses performances diminuent après l'entraînement jusqu'à un certain stade (phénomène de saturation), donc la raison car ce phénomène est quoi ? Peut-il être surmonté et exploité pour améliorer les performances des petits modèles de langage ?

Les derniers progrès dans le domaine de la modélisation du langage résident dans le pré-entraînement de réseaux de neurones hautement paramétrés sur des corpus de textes Web à très grande échelle. En pratique, l’utilisation d’un tel modèle pour la formation et l’inférence peut s’avérer coûteuse, ce qui incite à utiliser des modèles alternatifs plus petits. Cependant, il a été observé que les modèles plus petits peuvent souffrir d'une saturation et d'un phénomène caractérisé par une diminution des capacités et un plateau à un stade avancé de la formation.

Un article récent a révélé que ce phénomène de somme de saturation peut s'expliquer par un décalage entre la dimensionnalité latente des modèles plus petits et le rang élevé de la distribution de probabilité du contexte cible. Cette inadéquation affecte les performances des têtes de prédiction linéaire utilisées dans ces modèles en exploitant les performances des modèles appelés goulots d'étranglement softmax.

Lien papier : https://arxiv.org/pdf/2404.07647.pdf

Cet article mesure l'impact du goulot d'étranglement softmax dans différents contextes et constate que les modèles basés sur moins de 1000 dimensions cachées ont tendance à être pré Les représentations latentes dégénérées formées sont adoptées à un stade ultérieur, ce qui entraîne une réduction des performances d'évaluation.

Introduction

Le problème de dégradation de la représentation est un phénomène courant qui affecte divers modes tels que les méthodes d'apprentissage auto-supervisées de données textuelles. Les observations de représentations intermédiaires de modèles de langage révèlent leur variabilité à faible angle (ou anisotropie) ou des dimensions inhabituelles qui surviennent au cours de l'entraînement. Cependant, ces observations sont majoritairement réalisées sur des modèles à relativement petite échelle et aux dimensions comparables aux modèles familiaux tels que le BERT ou le GPT-2.

Ces modèles consistent généralement en un réseau neuronal f_θ qui accepte une séquence de jetons :

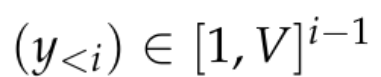
et génère une représentation de contexte relativement basse dimensionnelle dans R^d, où d est la dimension cachée du modèle. Ils s’appuient ensuite sur une tête de modélisation du langage qui produit le logarithme des probabilités des jetons de contexte. Un choix courant pour une tête de modélisation de langage est une couche linéaire avec des paramètres W ∈ R^(V×d), où V est le nombre de jetons possibles. Ainsi, la distribution de probabilité résultante pour le prochain jeton est 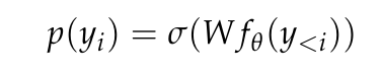où σ est la fonction softmax.

Dans le domaine de la modélisation du langage, la tendance actuelle est d'étendre la méthode de pré-entraînement génératif introduite par GPT-2, ce qui signifie entraîner des modèles neuronaux composés de milliards de paramètres sur un énorme corpus de texte Web. Cependant, la formation et l'application de ces modèles hautement paramétrés soulèvent des problèmes liés à l'énergie et au matériel, ce qui nécessite de trouver des moyens d'atteindre des niveaux de performances similaires avec des modèles plus petits.

Cependant, l'évaluation de la suite de modèles Pythia montre que l'entraînement de petits modèles sur de très grands corpus peut conduire à une saturation, se manifestant par une dégradation des performances tard dans la pré-entraînement. Cet article explore ce phénomène de saturation à travers le prisme de la dégradation de la représentation et constate qu'il existe une forte corrélation entre les deux phénomènes, tout en démontrant en outre que la dégradation de la représentation se produit dans les têtes de modélisation linguistique des petits modèles et a été démontrée à la fois théoriquement et empiriquement ci-dessus. comment les en-têtes de modélisation de langage linéaire peuvent devenir un goulot d'étranglement en termes de performances pour les architectures basées sur de petites dimensions cachées.

Phénomène de saturation du modèle linguistique

Cet article vérifie d'abord que la saturation des performances des points de contrôle Pythia peut effectivement être observée et quantifiée, car ce sont les seuls points de contrôle intermédiaires publiés pour une gamme de tailles de modèles. Cet article mesure l'entropie croisée des points de contrôle Pythia sur 50 000 jetons échantillonnés aléatoirement à partir de leur ensemble de données de pré-entraînement (c'est-à-dire The Pile).

On voit clairement sur la figure 1a que même le modèle à 410 millions de paramètres rencontre une saturation, se manifestant par une augmentation de la perte dans le domaine au stade de la formation avancée.

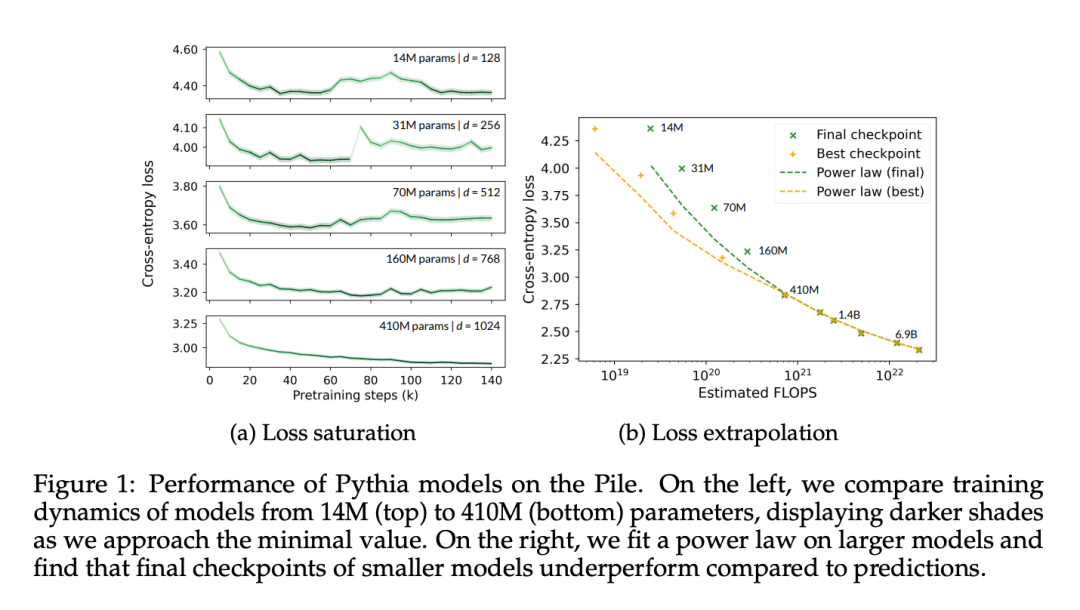
Dans la figure 1b, cet article ajuste les points de données du modèle à partir de 410 millions de paramètres selon la méthode de Hoffmann et al (2022), et optimise uniquement les constantes liées au modèle (A et α). , Tout en réutilisant toutes les autres valeurs (B = 410,7, β = 0,28, E = 1,69). Nous passons ici en revue la relation entre le nombre de paramètres N et le nombre de jetons T donnée par Hoffmann et al (2022) :

Cet article a révélé que les paramètres optimaux sont A = 119,09 et α = 0,246. Les auteurs montrent des courbes ajustées du nombre de jetons correspondant aux points de contrôle optimaux et finaux. On peut observer que la performance du point de contrôle final est en moyenne inférieure d’environ 8 % à la valeur extrapolée. Le point de contrôle de minimisation des pertes (optimal) devrait être inférieur à celui de la méthode d'extrapolation en raison d'un refroidissement incomplet du taux d'apprentissage, mais ses performances ne sont qu'environ 4 % inférieures à celles de la méthode d'extrapolation.

Un phénomène similaire de saturation des performances a également été observé dans l'ensemble de données utilisé pour l'évaluation de l'outil d'évaluation du modèle de langage (LM Evaluation Harness), comme le montre le tableau 1.

La saturation des performances est la saturation du rang

Anisotropie d'échelle

L'anisotropie est une forme courante de dégradation de la représentation observée dans divers petits modèles de langage. Elle comprend une réduction de la variabilité angulaire de la distribution de la représentation dans un domaine spécifique. couche. Des recherches antérieures (Ethayarajh, 2019 ; Godey et al., 2024) ont noté que presque toutes les couches de petits modèles de langage déformés sont anisotropes. Une manière courante de mesurer l'anisotropie dans un ensemble de représentations vectorielles H est la similarité cosinus moyenne :

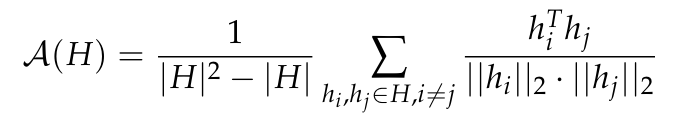
Cependant, il n'est pas clair si l'anisotropie affecte les modèles avec plus d'un milliard de paramètres. Pour résoudre ce problème, cet article calcule la similarité cosinusoïdale moyenne entre les couches pour une série de représentations intermédiaires modèles, à savoir GPT-2, OPT, Pythia et Gemma ; Cet article utilise un sous-échantillon de The Pile car il est supposé que le domaine de cet ensemble de données inclut ou correspond au domaine des ensembles de données pré-entraînés utilisés dans ces suites.

Dans la figure 2, on peut observer que la plupart des couches de la plupart des modèles Transformer sont dans une certaine mesure anisotropes, quelle que soit leur échelle. Cependant, il semble y avoir une dichotomie dans la dernière couche, où le modèle est soit presque isotrope, soit fortement anisotrope. Cet article note que cette dichotomie est cohérente avec l'un des phénomènes de saturation de la suite Pythia, où seuls les modèles comportant 160 millions de paramètres ou moins sont affectés par l'anisotropie de la dernière couche.

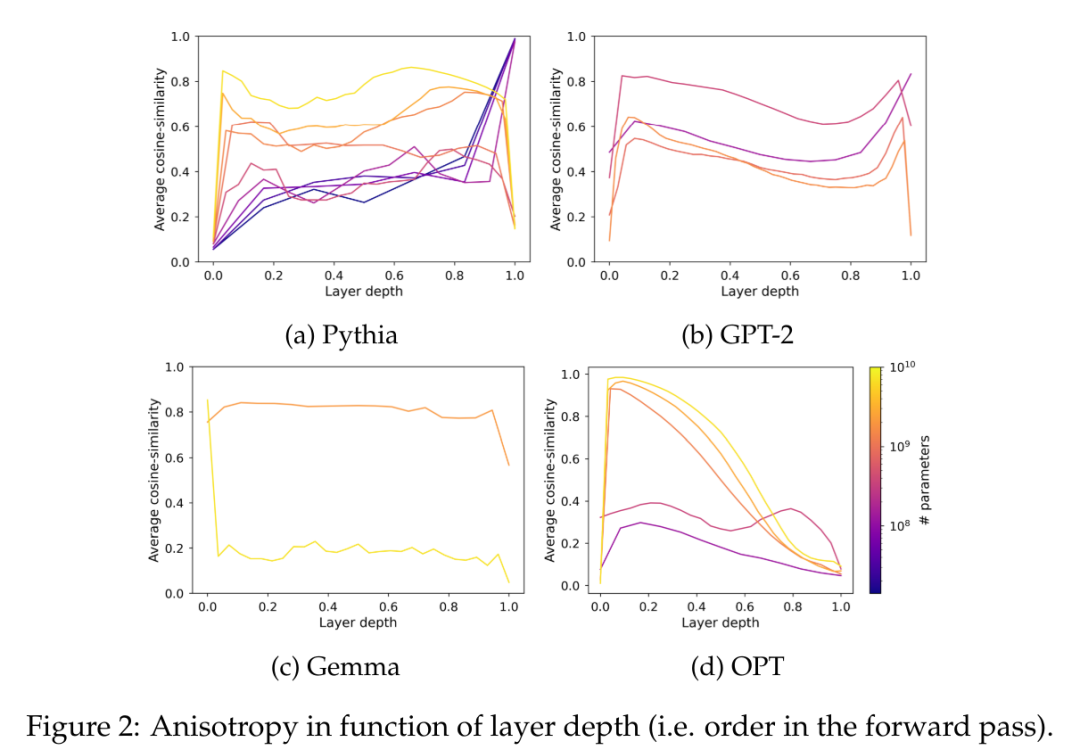
Cet article étudie la dynamique d'entraînement de l'anisotropie dans la suite Pythia et la compare au phénomène de saturation de la figure 3.

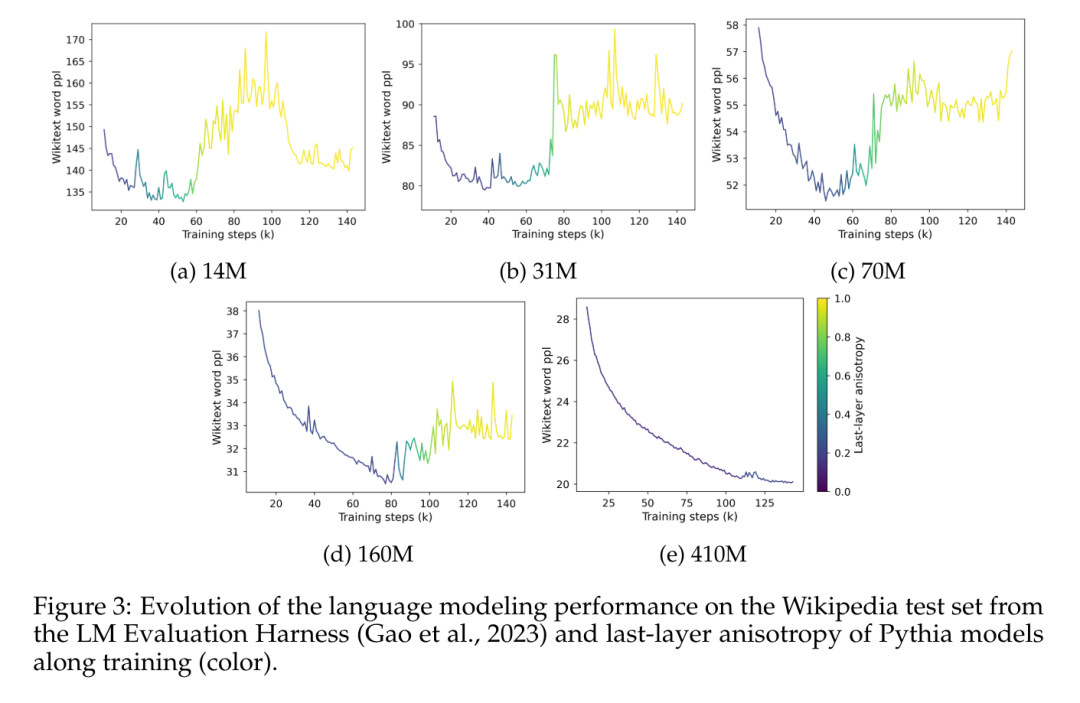
La figure 3 démontre clairement la corrélation claire entre l'émergence de la saturation des performances et l'émergence de l'anisotropie dans la représentation de la dernière couche du modèle. Il montre également une augmentation soudaine de l’anisotropie près du point de saturation pendant l’entraînement. Ce que l’on observe ici, c’est qu’au sein d’un corpus spécifique dans un domaine, le modèle perd rapidement ses performances en cas de saturation et ne semble jamais se remettre complètement de cette explosion.

Saturation des valeurs singulières

La similarité moyenne du cosinus est une mesure précieuse de l'uniformité de la distribution, mais l'inclusion d'autres mesures peut aider à mieux capturer la complexité de certaines variétés. De plus, il se concentre uniquement sur les intégrations de sortie du modèle de langage et non sur leurs poids. Cette section étend l'analyse de cet article en étudiant la distribution de valeurs singulières des têtes de modélisation du langage pour relier les observations empiriques aux conclusions théoriques de cet article.

La figure 4 montre la distribution des valeurs singulières le long du poids W de la couche de prédiction finale pendant l'entraînement :

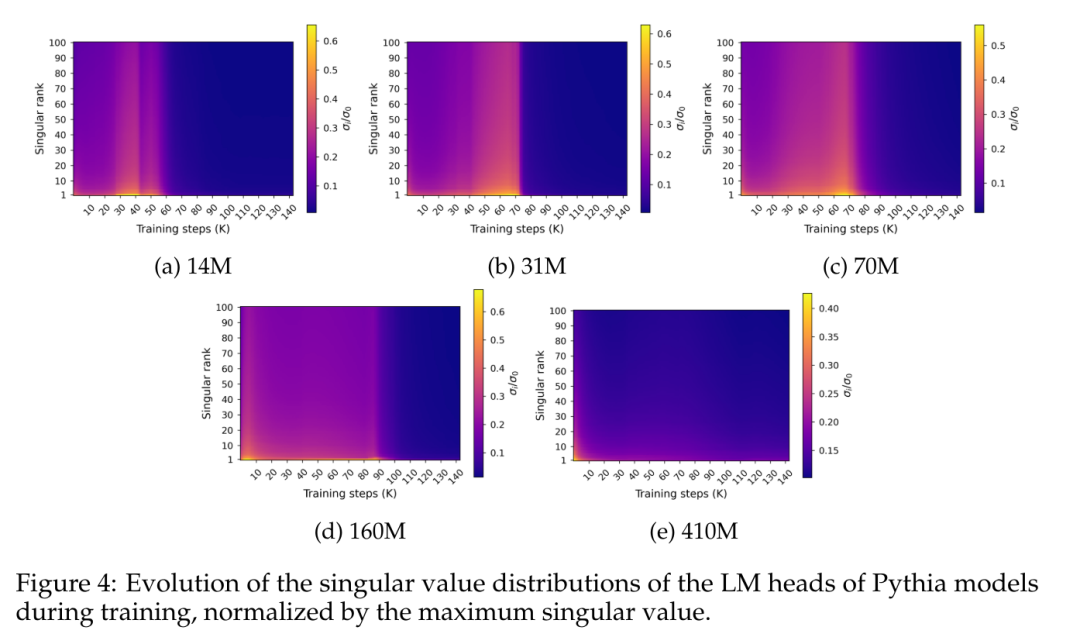
La figure 4 révèle un modèle spécifique de saturation spectrale qui se produit approximativement simultanément avec la saturation des performances. La figure montre que la distribution des valeurs singulières s'aplatit progressivement au cours du processus de formation, atteignant presque l'uniformité, puis évolue soudainement vers une distribution en pointes avec la plus grande valeur singulière relativement élevée par rapport aux autres distributions.

Pour quantifier ce comportement avec plus de précision, cet article utilise la métrique d'entropie singulière, calculée comme la divergence de Kullback-Leibler entre la distribution normalisée des valeurs singulières et la distribution uniforme.

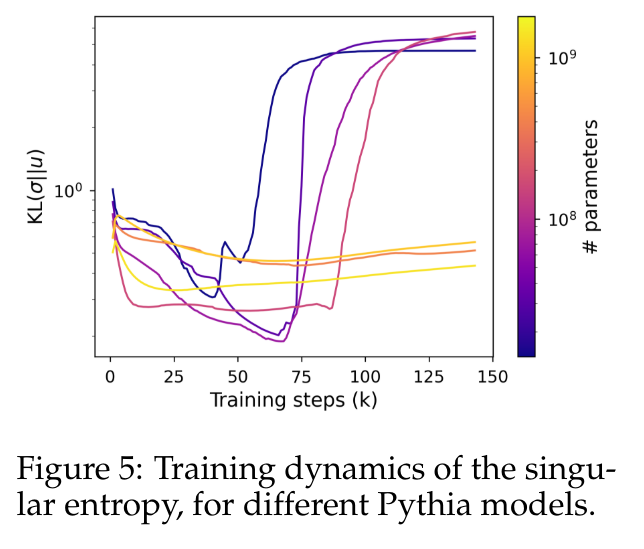
La figure 5 montre comment la distribution singulière évolue différemment pour un modèle utilisant moins de 410 millions de paramètres par rapport à un modèle utilisant des paramètres plus grands. Les têtes de petits modèles voient leurs distributions de valeurs singulières devenir progressivement plus uniformes, jusqu'à ce qu'elles se dégradent soudainement, ce qui est là encore en corrélation avec une dégradation des performances du modèle de langage. La distribution des valeurs singulières des modèles plus grands a tendance à être plus stable et ne présente pas de modèle monotone évident tout au long de la formation.

Gout d'étranglement de Softmax et dimension du langage

Dimension intrinsèque du langage naturel

Intuitivement parlant, le phénomène de saturation de la distribution de valeurs singulières observé ci-dessus ne s'applique qu'aux modèles plus petits, ce qui pose problème pour la tête LM. Les dimensions impliqués dans l’optimisation ont été interrogés. Cette section propose de mesurer empiriquement la valeur critique du rang d'un responsable LM et d'estimer les dimensions de la distribution de probabilité contextuelle à laquelle devrait correspondre la sortie de ce responsable.

Pour mesurer empiriquement l'impact du classement linéaire des chefs, cet article propose de former un chef restreint au rang sur des représentations contextuelles pré-entraînées dérivées de modèles de langage hautement paramétrés. Pour contrôler le rang maximum r, considérons une tête de la forme W = AB ∈ R^(V×d), où les coefficients de A ∈ R^(V×r) et B ∈ R^(r×d) partent de N(0 ,1) extrait (d est la dimension cachée du modèle). Le rang de cette matrice W est balayé sur une plage de valeurs contrainte par le paramètre r ∈ [1, d].

En gelant le modèle linguistique et en formant le responsable restreint au rang sur environ 150 millions de jetons tout en ajustant le taux d'apprentissage en fonction du nombre de paramètres pouvant être entraînés.

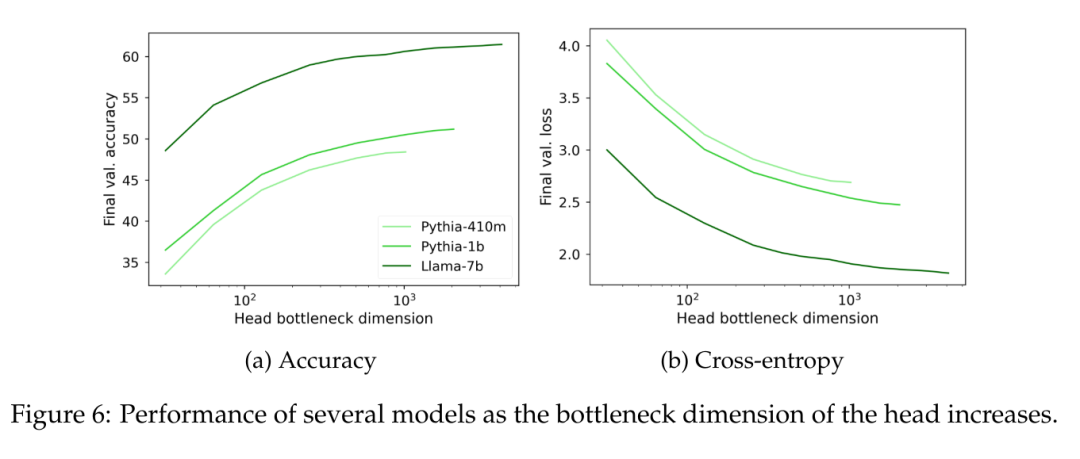
On peut observer sur la figure 6 que quelle que soit la taille du modèle, lorsque le rang de la tête de modélisation du langage W tombe en dessous de 1000, la perplexité commence à diminuer de manière significative. Cela implique que pour les modèles avec des dimensions cachées plus grandes, la tête ne constitue pas un goulot d'étranglement majeur en termes de performances, mais pour les modèles avec des dimensions cachées plus petites, elle peut nuire aux performances indépendamment de la qualité de la représentation de sortie.

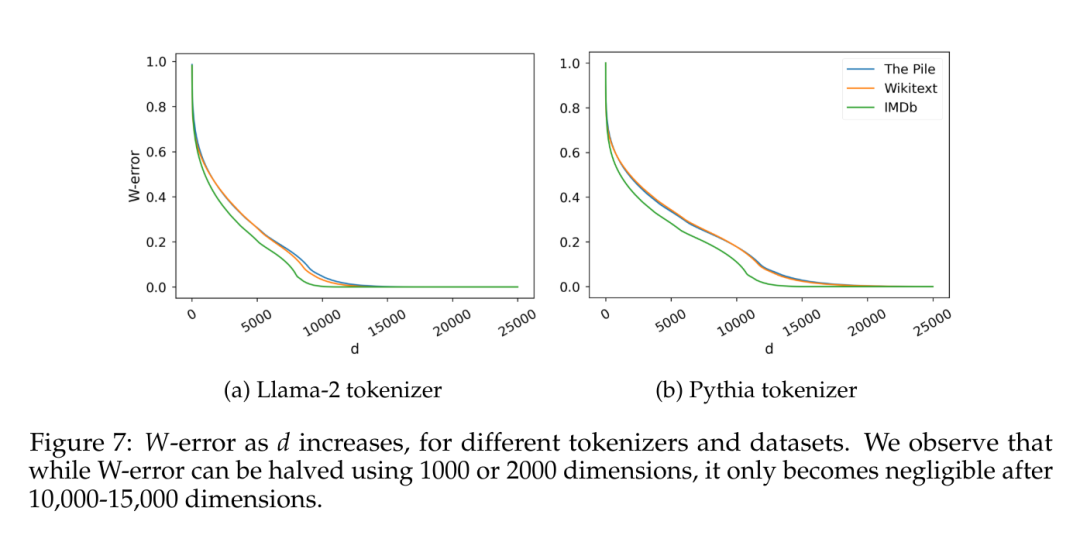
Un autre facteur intéressant est la dimensionnalité inhérente aux données estimées elles-mêmes. Afin d'éviter d'éventuels effets liés à un biais inductif spécifique, cet article a formé un modèle de langage naïf de 5 grammes sur plusieurs ensembles de données avec une couverture différente (IMDb, Wikitext et The Pile), en utilisant deux tailles de vocabulaire différentes Tokenizer (30 000 jetons pour. Llama-2, 50 000 jetons pour la Pythie). Étant donné C observé 5 grammes, cet article considère la matrice W ∈ R^(C×V), où chaque ligne est la distribution de probabilité de jetons possibles étant donné 4 jetons, et calcule leurs distributions de valeurs singulières, comme Terashima (2003).

La figure 7 rapporte l'erreur W, l'erreur d'approximation minimale pour une matrice W de rang d prédite par le théorème d'Eckart-Young-Mirsky (voir Lemme 5.2) et normalisée à la norme de Frobenius de W.

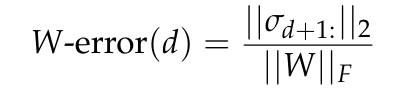
Goulot d'étranglement théorique

Dans le même temps, le rang estimé de W ne peut être ignoré par rapport à l'ordre de grandeur conventionnel des dimensions cachées. Ici, nous analyserons le lien entre les dimensions et les performances d'une tête de modélisation de langage linéaire idéale d'un point de vue théorique.

Cette section vise à identifier un lien formel entre les dimensions inhérentes aux distributions de contexte et les goulots d'étranglement des performances qui peuvent être attribués à la dimensionnalité inférieure des représentations de sortie du modèle de langage. À cette fin, une tête de modélisation de langage optimisée sur une représentation de contexte idéal est conçue, et la relation entre ses propriétés spectrales et l'écart de performance qui apparaît lors de la formation d'une tête de rang inférieur sur la même représentation est explorée.

Pour plus de détails sur la recherche, veuillez consulter l’article original.

Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!