 Périphériques technologiques
Périphériques technologiques
 IA
IA
 MLP a été tué du jour au lendemain ! Le MIT Caltech et d'autres KAN révolutionnaires battent des records et découvrent des théorèmes mathématiques qui écrasent DeepMind
MLP a été tué du jour au lendemain ! Le MIT Caltech et d'autres KAN révolutionnaires battent des records et découvrent des théorèmes mathématiques qui écrasent DeepMind
MLP a été tué du jour au lendemain ! Le MIT Caltech et d'autres KAN révolutionnaires battent des records et découvrent des théorèmes mathématiques qui écrasent DeepMind
Du jour au lendemain, le paradigme du machine learning va changer !
Aujourd'hui, l'infrastructure qui domine le domaine de l'apprentissage profond est le perceptron multicouche (MLP) - qui place des fonctions d'activation sur les neurones.
Alors, à part cela, y a-t-il un nouvel itinéraire que nous pourrions emprunter ?


Aujourd'hui encore, des équipes du MIT, du California Institute of Technology, de la Northeastern University et d'autres institutions ont publié une nouvelle structure de réseau neuronal : Kolmogorov-Arnold Networks (KAN).

Les chercheurs ont apporté une modification simple au MLP, c'est-à-dire en déplaçant la fonction d'activation apprenable des nœuds (neurones) vers les bords (poids) !

Adresse papier : https://arxiv.org/pdf/2404.19756
Ce changement peut sembler sans fondement au premier abord, mais il a quelque chose à voir avec les « théories de l'approximation » en mathématiques Un lien assez profond.
Il s'avère que la représentation de Kolmogorov-Arnold correspond à un réseau à deux couches, avec des fonctions d'activation apprenables sur les bords, pas sur les nœuds.
Inspirés par le théorème de la représentation, des chercheurs ont utilisé des réseaux de neurones pour paramétrer explicitement la représentation de Kolmogorov-Arnold.
Il convient de mentionner que l'origine du nom KAN est de commémorer les deux grands mathématiciens Andrey Kolmogorov et Vladimir Arnold.

Les résultats expérimentaux montrent que KAN a des performances supérieures à celles du MLP traditionnel, améliorant la précision et l'interprétabilité des réseaux de neurones.

La chose la plus inattendue est que la visualisation et l'interactivité de KAN lui confèrent une valeur d'application potentielle dans la recherche scientifique et peuvent aider les scientifiques à découvrir de nouvelles lois mathématiques et physiques.
Dans la recherche, l'auteur a utilisé KAN pour redécouvrir les lois mathématiques de la théorie des nœuds !
De plus, KAN a répliqué les résultats de DeepMind en 2021 avec un réseau et une automatisation plus petits.

En physique, KAN peut aider les physiciens à étudier la localisation d'Anderson (qui est une transition de phase en physique de la matière condensée).
D'ailleurs, tous les exemples de KAN de l'étude (sauf le scanning des paramètres) peuvent être reproduits en moins de 10 minutes sur un seul CPU.

L'émergence de KAN a directement remis en question l'architecture MLP qui avait toujours dominé le domaine de l'apprentissage automatique et provoqué un tollé dans l'ensemble du réseau.
Une nouvelle ère d'apprentissage automatique a commencé
Certaines personnes disent qu'une nouvelle ère d'apprentissage automatique a commencé !

Le chercheur Google DeepMind a déclaré : « Kolmogorov-Arnold frappe encore ! Un fait peu connu : ce théorème est apparu dans un article fondateur sur les réseaux neuronaux invariants par permutation (ensembles de profondeur), montrant cette représentation Une connexion complexe à la manière dont les ensembles/ Les agrégateurs GNN sont construits (comme cas particulier)".

Une toute nouvelle architecture de réseau de neurones est née ! KAN va radicalement changer la façon dont l’intelligence artificielle est formée et affinée.


Est-ce que l'IA est entrée dans l'ère 2.0 ?

Certains internautes ont utilisé un langage populaire pour créer une métaphore vivante de la différence entre KAN et MLP :
Le réseau Kolmogorov-Arnold (KAN) est comme un réseau tridimensionnel qui peut préparer n'importe quel gâteau . Une recette de gâteau en couches, tandis qu'un Perceptron multicouche (MLP) est un gâteau personnalisé avec un nombre variable de couches. MLP est plus complexe mais plus général, tandis que KAN est statique mais plus simple et plus rapide pour une seule tâche.

L'auteur de l'article, le professeur Max Tegmark du MIT, a déclaré que le dernier article montre qu'une architecture complètement différente du réseau neuronal standard peut obtenir de meilleurs résultats avec moins de paramètres lorsqu'il s'agit de problèmes physiques et mathématiques intéressants. . Haute précision.

Ensuite, regardons comment KAN, qui représente l'avenir du deep learning, est mis en œuvre ?
KAN de retour sur la table de poker
Base théorique de KAN
Le théorème de la représentation de Kolmogorov-Arnold stipule que si f est défini sur un domaine borné Une fonction continue à plusieurs variables, alors la fonction peut être exprimée comme une combinaison finie de plusieurs fonctions continues additives à une variable.

Pour l'apprentissage automatique, le problème peut être décrit comme suit : le processus d'apprentissage d'une fonction de grande dimension peut être simplifié en l'apprentissage d'une fonction unidimensionnelle d'une quantité polynomiale.
Mais ces fonctions unidimensionnelles peuvent être non lisses, voire fractales, et peuvent ne pas être apprises en pratique. C'est précisément à cause de ce « comportement pathologique » que le théorème de représentation de Kolmogorov-Arnold dans le domaine des machines. l'apprentissage, il est fondamentalement condamné à « mort », c'est-à-dire que la théorie est correcte, mais elle est inutile dans la pratique.
Dans cet article, les chercheurs sont toujours optimistes quant à l'application de ce théorème dans le domaine de l'apprentissage automatique, et proposent deux améliorations :
1 Dans l'équation originale, il n'y a que deux couches de non-linéarité et une couche cachée (2n+1), qui peut généraliser le réseau à une largeur et une profondeur arbitraires
2 La plupart des fonctions dans la science et la vie quotidienne sont pour la plupart lisses et ont des structures combinatoires clairsemées, ce qui peut aider à former un Kolmogorov- lisse ; Représentation d'Arnold. À l’instar de la différence entre physiciens et mathématiciens, les physiciens sont davantage préoccupés par les scénarios typiques, tandis que les mathématiciens se préoccupent davantage des pires scénarios.
Architecture KAN
L'idée centrale de la conception du réseau Kolmogorov-Arnold (KAN) est de transformer le problème d'approximation de fonctions multivariables en problème d'apprentissage d'un ensemble de fonctions à variable unique. Dans ce cadre, chaque fonction univariée peut être paramétrée avec une B-spline, une courbe polynomiale locale par morceaux dont les coefficients peuvent être appris.

Afin d'étendre plus profondément et plus largement le réseau à deux couches du théorème original, les chercheurs ont proposé une version plus "généralisée" du théorème pour soutenir la conception de KAN :
Influencé par le structure empilée des MLP Inspiré par l'amélioration de la profondeur du réseau, l'article introduit également un concept similaire, la couche KAN, qui consiste en une matrice de fonctions unidimensionnelle, chaque fonction a des paramètres pouvant être entraînés.

Selon le théorème de Kolmogorov-Arnold, la couche KAN d'origine se compose de fonctions internes et de fonctions externes, correspondant respectivement à différentes dimensions d'entrée et de sortie. Cette méthode de conception d'empilement de couches KAN non seulement s'étend, mais améliore également la profondeur. des KAN et maintient l'interprétabilité et l'expressivité du réseau. Chaque couche est composée de fonctions à variable unique, et les fonctions peuvent être apprises et comprises indépendamment.
f dans la formule suivante est équivalent à KAN

Détails de mise en œuvre
Bien que le concept de conception de KAN semble simple et repose uniquement sur l'empilement, il n'est pas facile à optimiser, ont également déclaré des chercheurs. appris quelques techniques au cours du processus de formation.
1. Fonction d'activation résiduelle : En introduisant une combinaison de fonction de base b(x) et de fonction spline, et en utilisant le concept de connexion résiduelle pour construire la fonction d'activation ϕ(x), cela contribue à la stabilité de l'entraînement. processus.

2. Échelles d'initialisation (échelles) : L'initialisation de la fonction d'activation est réglée sur une fonction spline proche de zéro, et le poids w utilise la méthode d'initialisation Xavier, qui permet de maintenir la stabilité du gradient dès les premiers stades de la formation.
3. Mettez à jour la grille spline : étant donné que la fonction spline est définie dans un intervalle délimité et que la valeur d'activation peut dépasser cet intervalle pendant le processus de formation du réseau neuronal, la mise à jour dynamique de la grille spline peut garantir que la fonction spline fonctionne toujours. dans la plage appropriée.
Paramètres
1. Profondeur du réseau : L
2 Largeur de chaque couche : N
3. Chaque fonction spline est basée sur des intervalles G (points de grille des réseaux G+1), ordre k (généralement k = 3)
Donc, la quantité de paramètres de KAN est d'environ 
À titre de comparaison, la quantité de paramètres de MLP est O(L*N^2), ce qui semble être meilleur que KAN est plus efficace, mais les KAN peuvent utiliser des largeurs de couche (N) plus petites, ce qui améliore non seulement les performances de généralisation, mais également l'interprétabilité.
En quoi KAN est-il meilleur que MLP ?
Des performances plus fortes
Pour vérifier la plausibilité, les chercheurs ont construit cinq exemples connus pour avoir une représentation fluide de KA (Kolmogorov-Arnold) en tant qu'ensemble de données de validation, en augmentant le réseau toutes les 200 étapes. Les KAN sont formés de manière grille. , couvrant la plage de G comme {3,5,10,20,50,100,200,500,1000}
Utilisation de MLP avec différentes profondeurs et largeurs comme modèles de base, et les KAN et les MLP utilisent l'algorithme LBFGS. Un total de 1 800 étapes ont été formés, et le RMSE a été utilisé comme indicateur de comparaison.

Comme vous pouvez le voir d'après les résultats, la courbe de KAN est plus instable, peut converger rapidement et atteint un état stable et elle est meilleure que la courbe d'échelle de MLP, en particulier dans les situations de grande dimension ;
On peut également constater que les performances du KAN à trois couches sont beaucoup plus fortes que celles du KAN à deux couches, ce qui indique que les KAN plus profonds ont des capacités d'expression plus fortes, conformément aux attentes.
Explication interactive de KAN
Les chercheurs ont conçu une expérience de régression simple pour montrer que les utilisateurs peuvent obtenir les résultats les plus interprétables lors de l'interaction avec KAN.

En supposant que l'utilisateur souhaite connaître la formule symbolique, un total de 5 étapes interactives sont nécessaires.

Étape 1 : Entraînement avec sparsification.
À partir d'un KAN entièrement connecté, un entraînement avec une régularisation clairsemée peut rendre le réseau plus clairsemé, de sorte qu'on peut constater que 4 des 5 neurones de la couche cachée semblent n'avoir aucun effet.
Étape 2 : Élagage
Après l'élagage automatique, jetez tous les neurones cachés inutiles, en ne laissant qu'un seul KAN, et faites correspondre la fonction d'activation à la fonction de signe connue.
Étape 3 : Configurer les fonctions symboliques
En supposant que l'utilisateur puisse deviner correctement ces formules symboliques en regardant le graphique KAN, elles peuvent être définies directement

Si l'utilisateur n'a aucune connaissance du domaine ou ne sait pas quelles fonctions symboliques pourrait être la fonction d'activation, les chercheurs fournissent une fonction suggest_symbolic pour suggérer des candidats symboliques.
Étape 4 : Formation complémentaire
Une fois que toutes les fonctions d'activation dans le réseau sont symbolisées, les seuls paramètres restants sont les paramètres affines, continuez à entraîner les paramètres affines lorsque vous voyez la perte de précision de la machine (précision de la machine) ; , vous réalisez que le modèle a trouvé la bonne expression symbolique.
Étape 5 : Formule symbolique de sortie
Utilisez Sympy pour calculer la formule symbolique du nœud de sortie et vérifier la bonne réponse.
Vérification de l'interprétabilité
Les chercheurs ont d'abord conçu six échantillons dans un ensemble de données de jouets supervisé pour démontrer les capacités de structure combinatoire du réseau KAN sous des formules symboliques.

On peut voir que KAN a appris avec succès la bonne fonction de variable unique, et grâce à la visualisation, cela peut expliquer le processus de réflexion de KAN.
Dans un cadre non supervisé, l'ensemble de données contient uniquement la caractéristique d'entrée x. En concevant la connexion entre certaines variables (x1, x2, x3), la capacité du modèle KAN à trouver des dépendances entre variables peut être testée.

À en juger par les résultats, le modèle KAN a réussi à trouver la dépendance fonctionnelle entre les variables, mais l'auteur a également souligné que les expériences sont toujours menées uniquement sur des données synthétiques et qu'une méthode plus systématique et contrôlable est nécessaire. pour découvrir des relations complètes.

Pareto Optimal
En ajustant des fonctions spéciales, les auteurs montrent la frontière de Pareto de KAN et MLP dans le plan couvert par le nombre de paramètres du modèle et la perte RMSE.
Parmi toutes les fonctions spéciales, KAN a toujours un meilleur front de Pareto que MLP.

Résoudre des équations aux dérivées partielles
Dans la tâche de résolution d'équations aux dérivées partielles, les chercheurs ont tracé les pertes au carré L2 et H1 entre les solutions prédites et vraies.
Dans la figure ci-dessous, les deux premiers sont la dynamique d'entraînement de la perte, et les troisième et quatrième sont la loi de Sacling du nombre de fonctions de perte.
Comme le montrent les résultats ci-dessous, KAN converge plus rapidement, a des pertes plus faibles et a une loi d'expansion plus raide que MLP.

Apprentissage continu, l'oubli catastrophique ne se produira pas
Nous savons tous que l'oubli catastrophique est un problème sérieux dans l'apprentissage automatique.
La différence entre les réseaux de neurones artificiels et le cerveau est que le cerveau possède différents modules qui fonctionnent localement dans l'espace. Lors de l'apprentissage d'une nouvelle tâche, la réorganisation structurelle ne se produit que dans les zones locales responsables de la compétence concernée, tandis que les autres domaines restent inchangés.
Or, la plupart des réseaux de neurones artificiels, dont MLP, n'ont pas cette notion de localité, ce qui peut être la raison d'un oubli catastrophique.
La recherche a prouvé que KAN a une plasticité locale et peut utiliser la localité des splines pour éviter un oubli catastrophique.
L'idée est très simple, puisque la spline est locale, l'échantillon n'affectera que certains coefficients de spline proches, tandis que les coefficients distants restent inchangés.
En revanche, étant donné que MLP utilise généralement une activation globale (telle que ReLU/Tanh/SiLU), tout changement local peut se propager de manière incontrôlable vers des régions distantes, détruisant les informations qui y sont stockées.
Les chercheurs ont adopté une tâche de régression unidimensionnelle (constituée de 5 pics gaussiens). Les données autour de chaque pic sont présentées au KAN et au MLP de manière séquentielle (plutôt qu'en même temps).
Les résultats sont présentés dans la figure ci-dessous. KAN reconstruit uniquement la zone où les données existent à l'étape actuelle, laissant la zone précédente inchangée.
Et MLP remodelera toute la zone après avoir vu de nouveaux échantillons de données, conduisant à un oubli catastrophique.

J'ai découvert la théorie des nœuds et les résultats ont dépassé DeepMind
Que signifie la naissance de KAN pour les futures applications de l'apprentissage automatique ?
La théorie des nœuds est une discipline de la topologie de basse dimension. Elle révèle les problèmes topologiques des tri-variétés et des quadri-variétés et a de nombreuses applications dans des domaines tels que la biologie et l'informatique quantique topologique.

En 2021, l'équipe DeepMind a utilisé l'IA pour prouver la théorie des nœuds pour la première fois dans la nature.

Adresse papier : https://www.nature.com/articles/s41586-021-04086-x
Dans cette étude, grâce à l'apprentissage supervisé et à des experts du domaine humain, de nouveaux théorèmes liés à invariants de nœuds algébriques et géométriques.
Autrement dit, la saillance du gradient a identifié les invariants clés du problème de supervision, ce qui a conduit les experts du domaine à proposer une conjecture qui a ensuite été affinée et prouvée.
À cet égard, l'auteur étudie si KAN peut obtenir de bons résultats interprétables sur le même problème pour prédire la signature des nœuds.
Dans l'expérience DeepMind, les principaux résultats de leur étude de l'ensemble de données de la théorie des nœuds sont :
1 En utilisant la méthode d'attribution de réseau, on constate que la signature  dépend principalement de la distance intermédiaire
dépend principalement de la distance intermédiaire  et de la distance longitudinale λ.
et de la distance longitudinale λ.
2 , traitant la signature comme une sortie.  Semblable à la configuration dans DeepMind, les signatures (nombres pairs) sont codées sous forme de vecteurs uniques et le réseau est entraîné avec une perte d'entropie croisée.
Semblable à la configuration dans DeepMind, les signatures (nombres pairs) sont codées sous forme de vecteurs uniques et le réseau est entraîné avec une perte d'entropie croisée.  Les résultats ont révélé qu'un très petit KAN peut atteindre une précision de test de 81,6 %, tandis que le 300MLP à 4 couches de DeepMind n'atteint qu'une précision de test de 78 %.
Les résultats ont révélé qu'un très petit KAN peut atteindre une précision de test de 81,6 %, tandis que le 300MLP à 4 couches de DeepMind n'atteint qu'une précision de test de 78 %. 
Comme le montre le tableau ci-dessous, KAN (G = 3, k = 3) a environ 200 paramètres, tandis que MLP a environ 300 000 paramètres.
Il convient de noter que KAN n'est pas seulement plus précis ; Dans le même temps, les paramètres sont plus efficaces que MLP.
En termes d'interprétabilité, les chercheurs ont adapté la transparence de chaque activation en fonction de sa taille, de sorte qu'il était immédiatement clair, sans attribution de caractéristiques, quelles variables d'entrée étaient importantes.
Ensuite, KAN est formé sur trois variables importantes et obtient une précision de test de 78,2%. 
Comme suit, grâce à KAN, l'auteur a redécouvert trois relations mathématiques dans l'ensemble de données de nœuds.
La localisation physique d'Anderson a été résolue
 Et dans les applications physiques, KAN a également joué une grande valeur.
Et dans les applications physiques, KAN a également joué une grande valeur.
Anderson est un phénomène fondamental dans lequel le désordre dans un système quantique conduit à la localisation de la fonction d'onde électronique, stoppant ainsi toute transmission.

En revanche, en trois dimensions, une énergie critique forme une limite de phase qui sépare les états étendus des états localisés, appelée limite de mobilité.
Comprendre ces bords de mobilité est essentiel pour expliquer divers phénomènes fondamentaux tels que les transitions métal-isolant dans les solides et l'effet de localisation de la lumière dans les dispositifs photoniques.
L'auteur a découvert grâce à des recherches que les KAN permettent d'extraire très facilement les bords de mobilité, que ce soit numériquement ou symboliquement.
De toute évidence, KAN est devenu un assistant puissant et un collaborateur important pour les scientifiques.
Dans l'ensemble, KAN sera un modèle/outil utile pour l'IA+Science grâce à ses avantages en termes de précision, d'efficacité des paramètres et d'interprétabilité.
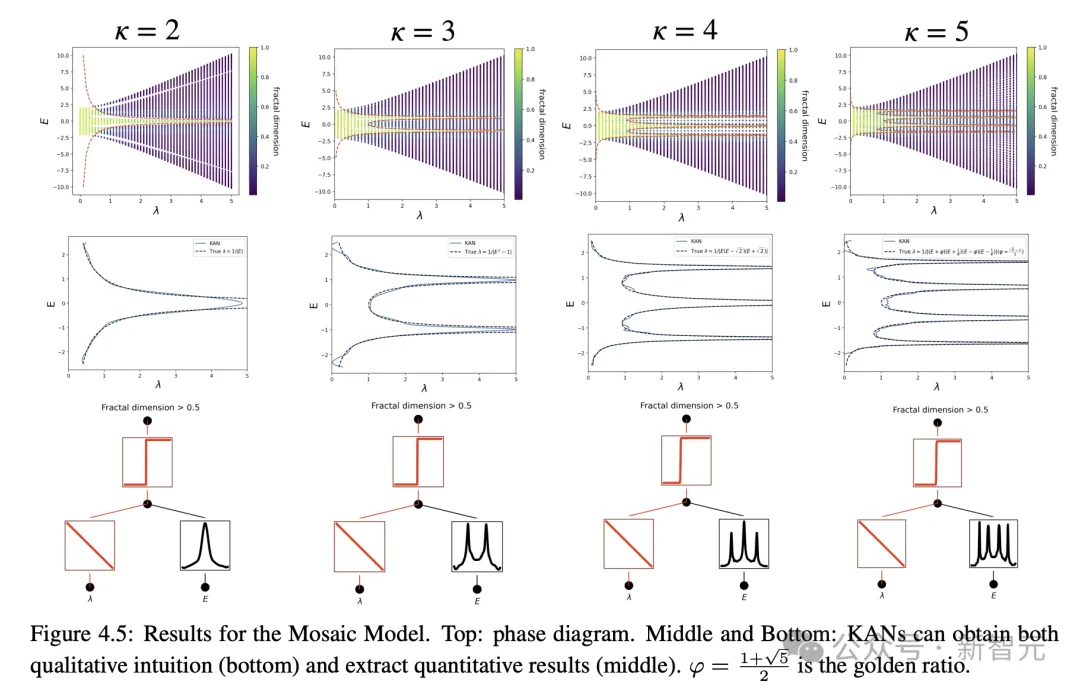
À l’avenir, d’autres applications du KAN dans le domaine scientifique doivent encore être explorées.

Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!

Outils d'IA chauds

Undresser.AI Undress
Application basée sur l'IA pour créer des photos de nu réalistes

AI Clothes Remover
Outil d'IA en ligne pour supprimer les vêtements des photos.

Undress AI Tool
Images de déshabillage gratuites

Clothoff.io
Dissolvant de vêtements AI

AI Hentai Generator
Générez AI Hentai gratuitement.

Article chaud

Outils chauds

Bloc-notes++7.3.1
Éditeur de code facile à utiliser et gratuit

SublimeText3 version chinoise
Version chinoise, très simple à utiliser

Envoyer Studio 13.0.1
Puissant environnement de développement intégré PHP

Dreamweaver CS6
Outils de développement Web visuel

SublimeText3 version Mac
Logiciel d'édition de code au niveau de Dieu (SublimeText3)
 Quelle méthode est utilisée pour convertir les chaînes en objets dans vue.js?
Apr 07, 2025 pm 09:39 PM
Quelle méthode est utilisée pour convertir les chaînes en objets dans vue.js?
Apr 07, 2025 pm 09:39 PM
Lors de la conversion des chaînes en objets dans vue.js, JSON.Parse () est préféré pour les chaînes JSON standard. Pour les chaînes JSON non standard, la chaîne peut être traitée en utilisant des expressions régulières et réduisez les méthodes en fonction du format ou du codé décodé par URL. Sélectionnez la méthode appropriée en fonction du format de chaîne et faites attention aux problèmes de sécurité et d'encodage pour éviter les bogues.
 Comment utiliser MySQL après l'installation
Apr 08, 2025 am 11:48 AM
Comment utiliser MySQL après l'installation
Apr 08, 2025 am 11:48 AM
L'article présente le fonctionnement de la base de données MySQL. Tout d'abord, vous devez installer un client MySQL, tel que MySQLWorkBench ou le client de ligne de commande. 1. Utilisez la commande MySQL-UROot-P pour vous connecter au serveur et connecter avec le mot de passe du compte racine; 2. Utilisez Createdatabase pour créer une base de données et utilisez Sélectionner une base de données; 3. Utilisez CreateTable pour créer une table, définissez des champs et des types de données; 4. Utilisez InsertInto pour insérer des données, remettre en question les données, mettre à jour les données par mise à jour et supprimer les données par Supprimer. Ce n'est qu'en maîtrisant ces étapes, en apprenant à faire face à des problèmes courants et à l'optimisation des performances de la base de données que vous pouvez utiliser efficacement MySQL.
 Vue.js Comment convertir un tableau de type de chaîne en un tableau d'objets?
Apr 07, 2025 pm 09:36 PM
Vue.js Comment convertir un tableau de type de chaîne en un tableau d'objets?
Apr 07, 2025 pm 09:36 PM
Résumé: Il existe les méthodes suivantes pour convertir les tableaux de chaîne Vue.js en tableaux d'objets: Méthode de base: utilisez la fonction de carte pour convenir à des données formatées régulières. Gameplay avancé: l'utilisation d'expressions régulières peut gérer des formats complexes, mais ils doivent être soigneusement écrits et considérés. Optimisation des performances: Considérant la grande quantité de données, des opérations asynchrones ou des bibliothèques efficaces de traitement des données peuvent être utilisées. MEILLEUR PRATIQUE: Effacer le style de code, utilisez des noms de variables significatifs et des commentaires pour garder le code concis.
 Comment définir le délai de Vue Axios
Apr 07, 2025 pm 10:03 PM
Comment définir le délai de Vue Axios
Apr 07, 2025 pm 10:03 PM
Afin de définir le délai d'expiration de Vue Axios, nous pouvons créer une instance AxiOS et spécifier l'option Timeout: dans les paramètres globaux: vue.prototype. $ Axios = axios.create ({timeout: 5000}); Dans une seule demande: ce. $ axios.get ('/ api / utilisateurs', {timeout: 10000}).
 Géospatial de Laravel: optimisation des cartes interactives et de grandes quantités de données
Apr 08, 2025 pm 12:24 PM
Géospatial de Laravel: optimisation des cartes interactives et de grandes quantités de données
Apr 08, 2025 pm 12:24 PM
Traiter efficacement 7 millions d'enregistrements et créer des cartes interactives avec la technologie géospatiale. Cet article explore comment traiter efficacement plus de 7 millions d'enregistrements en utilisant Laravel et MySQL et les convertir en visualisations de cartes interactives. Exigences initiales du projet de défi: extraire des informations précieuses en utilisant 7 millions d'enregistrements dans la base de données MySQL. Beaucoup de gens considèrent d'abord les langages de programmation, mais ignorent la base de données elle-même: peut-il répondre aux besoins? La migration des données ou l'ajustement structurel est-il requis? MySQL peut-il résister à une charge de données aussi importante? Analyse préliminaire: les filtres et les propriétés clés doivent être identifiés. Après analyse, il a été constaté que seuls quelques attributs étaient liés à la solution. Nous avons vérifié la faisabilité du filtre et établi certaines restrictions pour optimiser la recherche. Recherche de cartes basée sur la ville
 Comment résoudre MySQL ne peut pas être démarré
Apr 08, 2025 pm 02:21 PM
Comment résoudre MySQL ne peut pas être démarré
Apr 08, 2025 pm 02:21 PM
Il existe de nombreuses raisons pour lesquelles la startup MySQL échoue, et elle peut être diagnostiquée en vérifiant le journal des erreurs. Les causes courantes incluent les conflits de port (vérifier l'occupation du port et la configuration de modification), les problèmes d'autorisation (vérifier le service exécutant les autorisations des utilisateurs), les erreurs de fichier de configuration (vérifier les paramètres des paramètres), la corruption du répertoire de données (restaurer les données ou reconstruire l'espace de la table), les problèmes d'espace de la table InNODB (vérifier les fichiers IBDATA1), la défaillance du chargement du plug-in (vérification du journal des erreurs). Lors de la résolution de problèmes, vous devez les analyser en fonction du journal d'erreur, trouver la cause profonde du problème et développer l'habitude de sauvegarder régulièrement les données pour prévenir et résoudre des problèmes.
 Comment optimiser les performances de la base de données après l'installation de MySQL
Apr 08, 2025 am 11:36 AM
Comment optimiser les performances de la base de données après l'installation de MySQL
Apr 08, 2025 am 11:36 AM
L'optimisation des performances MySQL doit commencer à partir de trois aspects: configuration d'installation, indexation et optimisation des requêtes, surveillance et réglage. 1. Après l'installation, vous devez ajuster le fichier my.cnf en fonction de la configuration du serveur, tel que le paramètre innodb_buffer_pool_size, et fermer query_cache_size; 2. Créez un index approprié pour éviter les index excessifs et optimiser les instructions de requête, telles que l'utilisation de la commande Explication pour analyser le plan d'exécution; 3. Utilisez le propre outil de surveillance de MySQL (ShowProcessList, Showstatus) pour surveiller la santé de la base de données, et sauvegarde régulièrement et organisez la base de données. Ce n'est qu'en optimisant en continu ces étapes que les performances de la base de données MySQL peuvent être améliorées.
 Les ingénieurs de backend senior à distance (plates-formes) ont besoin de cercles
Apr 08, 2025 pm 12:27 PM
Les ingénieurs de backend senior à distance (plates-formes) ont besoin de cercles
Apr 08, 2025 pm 12:27 PM
Ingénieur backend à distance Emploi Vacant Société: Emplacement du cercle: Bureau à distance Type d'emploi: Salaire à temps plein: 130 000 $ - 140 000 $ Description du poste Participez à la recherche et au développement des applications mobiles Circle et des fonctionnalités publiques liées à l'API couvrant l'intégralité du cycle de vie de développement logiciel. Les principales responsabilités complètent indépendamment les travaux de développement basés sur RubyOnRails et collaborent avec l'équipe frontale React / Redux / Relay. Créez les fonctionnalités de base et les améliorations des applications Web et travaillez en étroite collaboration avec les concepteurs et le leadership tout au long du processus de conception fonctionnelle. Promouvoir les processus de développement positifs et hiérarchiser la vitesse d'itération. Nécessite plus de 6 ans de backend d'applications Web complexe





