 Périphériques technologiques
Périphériques technologiques
 IA
IA
 Régression quantile pour la prévision probabiliste de séries chronologiques
Régression quantile pour la prévision probabiliste de séries chronologiques
Régression quantile pour la prévision probabiliste de séries chronologiques
Ne changez pas le sens du contenu original, affinez le contenu, réécrivez le contenu et ne continuez pas à écrire. "La régression quantile répond à ce besoin, en fournissant des intervalles de prédiction avec des chances quantifiées. Il s'agit d'une technique statistique utilisée pour modéliser la relation entre une variable prédictive et une variable de réponse, en particulier lorsque la distribution conditionnelle de la variable de réponse présente un intérêt quand. Contrairement à la régression traditionnelle méthodes, la régression quantile se concentre sur l'estimation de l'ampleur conditionnelle de la variable de réponse plutôt que de la moyenne conditionnelle »
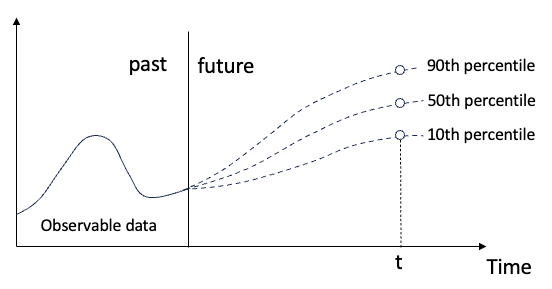 Figure (A) : Régression quantile
Figure (A) : Régression quantile
Concept de régression quantile
La régression quantile est une méthode de modélisation qui estime la. relation linéaire entre un ensemble de régresseurs X et les quantiles des variables expliquées Y.
Le modèle de régression existant est en fait une méthode d'étude de la relation entre la variable expliquée et la variable explicative. Ils se concentrent sur la relation entre les variables explicatives et les variables expliquées et sur leur distribution d'erreurs. La régression médiane et la régression quantile sont deux modèles de régression courants. Ils ont été proposés pour la première fois selon Koenker et Bassett (1978).
Le calcul de l'estimateur de régression des moindres carrés ordinaires est basé sur la minimisation de la somme des carrés résiduels. Le calcul de l'estimateur de régression quantile repose également sur la minimisation du résidu en valeur absolue sous une forme symétrique. Parmi eux, l'opération de régression médiane est l'estimateur des moindres écarts absolus (LAD, estimateur des moindres écarts absolus).
Avantages de la régression quantile
Expliquez l'image complète de la distribution conditionnelle de la variable expliquée. Elle analyse non seulement l'espérance conditionnelle (moyenne) de la variable expliquée, mais analyse également comment la variable explicative affecte la médiane et le quantile de la variable expliquée. variable expliquée. Nombre, etc. Les estimations des coefficients de régression aux différents quantiles sont souvent différentes, c'est-à-dire que les variables explicatives ont des effets différents sur différents quantiles. Par conséquent, les différents effets des différents quantiles des variables explicatives auront des effets différents sur les variables expliquées.
Par rapport à la méthode de moindre multiplication, la méthode d'estimation de la régression médiane est plus robuste aux valeurs aberrantes, et la régression quantile ne nécessite pas d'hypothèses fortes sur le terme d'erreur, donc pour les situations non normales, la distribution d'état et le coefficient de régression médian sont plus sains. Dans le même temps, l’estimation quantitative du système de régression quantile devient plus robuste.
Quels sont les avantages de la régression quantile par rapport à la simulation Monte Carlo ? Premièrement, la régression quantile estime directement l’ampleur conditionnelle de la variable de réponse compte tenu des prédicteurs. Cela signifie que, plutôt que de produire un grand nombre de résultats possibles comme une simulation de Monte Carlo, elle fournit une estimation d'une ampleur spécifique de la distribution de la variable de réponse. Ceci est particulièrement utile pour comprendre différents niveaux d’incertitude des prévisions, tels que les quintiles, les quartiles ou les magnitudes extrêmes. Deuxièmement, la régression quantile fournit une méthode d'estimation de l'incertitude de prédiction basée sur un modèle qui utilise des données d'observation pour estimer la relation entre les variables et faire des prédictions basées sur cette relation. En revanche, la simulation Monte Carlo repose sur la spécification de distributions de probabilité pour les variables d'entrée et la génération de résultats basés sur un échantillonnage aléatoire.
NeuralProphet propose deux techniques statistiques : (1) la régression quantile et (2) la régression quantile conforme. La technique de prédiction quantile conforme ajoute un processus d'étalonnage pour effectuer une régression quantile. Dans cet article, nous utiliserons le module de régression quantile de Neural Prophet pour faire des prédictions de régression quantile. Ce module ajoute un processus d'étalonnage pour garantir que les résultats de prédiction sont cohérents avec la distribution des données observées. Nous utiliserons le module de régression quantile de Neural Prophet dans ce chapitre.
Exigences environnementales
Installez NeuralProphet.
!pip install neuralprophet!pip uninstall numpy!pip install git+https://github.com/ourownstory/neural_prophet.git numpy==1.23.5
Importez les bibliothèques requises.
%matplotlib inlinefrom matplotlib import pyplot as pltimport pandas as pdimport numpy as npimport loggingimport warningslogging.getLogger('prophet').setLevel(logging.ERROR)warnings.filterwarnings("ignore")Dataset
Données de vélo partagées. L'ensemble de données est un ensemble de données multivarié qui contient la demande de location quotidienne ainsi que d'autres champs météorologiques tels que la température ou la vitesse du vent.
data = pd.read_csv('/bike_sharing_daily.csv')data.tail() Image (B) : Vélos partagés
Image (B) : Vélos partagés
Tracez le nombre de vélos partagés. Nous avons observé que la demande a augmenté la deuxième année et a suivi un modèle saisonnier.
# convert string to datetime64data["ds"] = pd.to_datetime(data["dteday"])# create line plot of sales dataplt.plot(data['ds'], data["cnt"])plt.xlabel("date")plt.ylabel("Count")plt.show()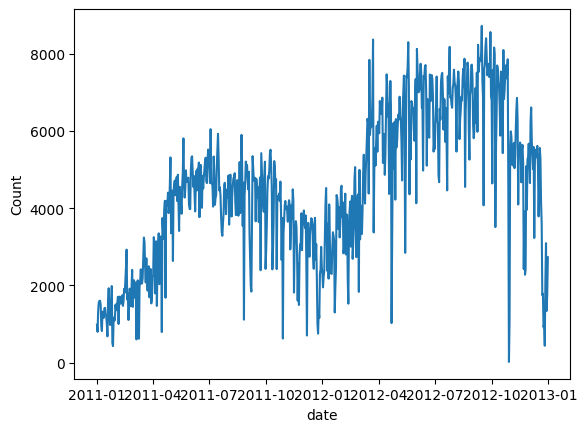 Image (C) : Demande quotidienne de location de vélos
Image (C) : Demande quotidienne de location de vélos
Effectuez la préparation des données la plus élémentaire pour la modélisation. NeuralProphet nécessite les noms de colonnes ds et y, qui sont les mêmes que Prophet.
df = data[['ds','cnt']]df.columns = ['ds','y']
构建分位数回归模型
直接在 NeuralProphet 中构建分位数回归。假设我们需要第 5、10、50、90 和 95 个量级的值。我们指定 quantile_list = [0.05,0.1,0.5,0.9,0.95],并打开参数 quantiles = quantile_list。
from neuralprophet import NeuralProphet, set_log_levelquantile_list=[0.05,0.1,0.5,0.9,0.95 ]# Model and predictionm = NeuralProphet(quantiles=quantile_list,yearly_seasnotallow=True,weekly_seasnotallow=True,daily_seasnotallow=False)m = m.add_country_holidays("US")m.set_plotting_backend("matplotlib")# Use matplotlibdf_train, df_test = m.split_df(df, valid_p=0.2)metrics = m.fit(df_train, validation_df=df_test, progress="bar")metrics.tail()分位数回归预测
我们将使用 .make_future_dataframe()为预测创建新数据帧,NeuralProphet 是基于 Prophet 的。参数 n_historic_predictions 为 100,只包含过去的 100 个数据点。如果设置为 True,则包括整个历史数据。我们设置 period=50 来预测未来 50 个数据点。
future = m.make_future_dataframe(df, periods=50, n_historic_predictinotallow=100) #, n_historic_predictinotallow=1)# Perform prediction with the trained modelsforecast = m.predict(df=future)forecast.tail(60)
预测结果存储在数据框架 predict 中。
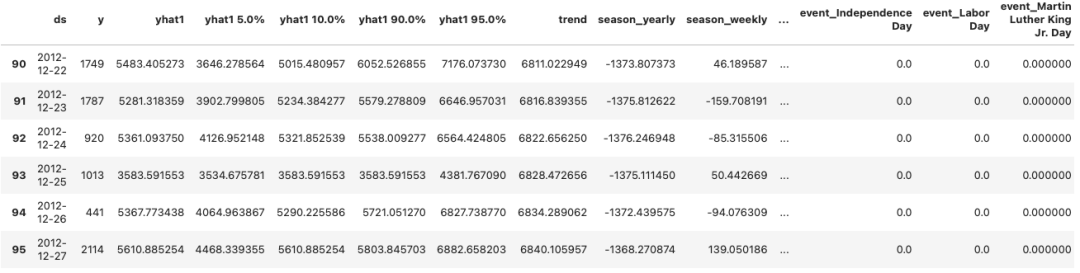 图 (D):预测
图 (D):预测
上述数据框架包含了绘制地图所需的所有数据元素。
m.plot(forecast, plotting_backend="plotly-static"#plotting_backend = "matplotlib")
预测区间是由分位数值提供的!
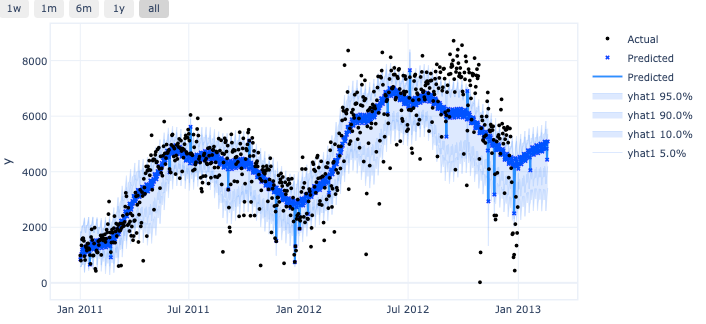 图 (E):分位数预测
图 (E):分位数预测
预测区间和置信区间的区别
预测区间和置信区间在流行趋势中很有帮助,因为它们可以量化不确定性。它们的目标、计算方法和应用是不同的。下面我将用回归来解释两者的区别。在图(F)中,我在左边画出了线性回归,在右边画出了分位数回归。
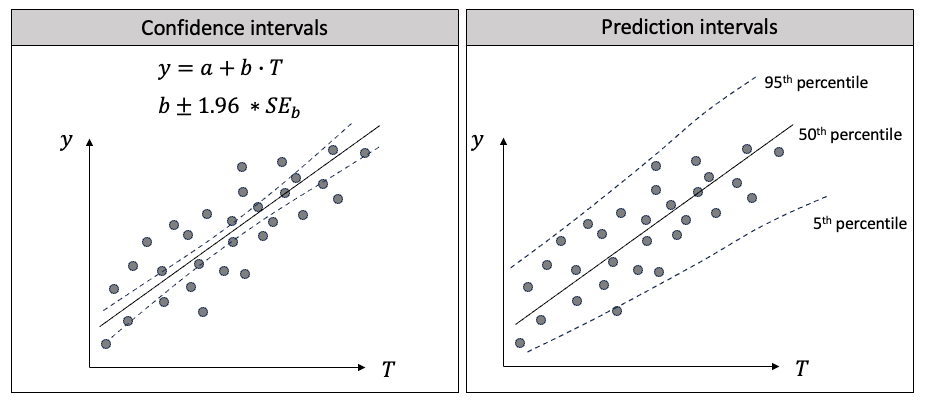 图(F):置信区间与预测区间的区别
图(F):置信区间与预测区间的区别
首先,它们的目标不同:
- 线性回归的主要目标是找到一条线,使预测值尽可能接近给定自变量值时因变量的条件均值。
- 分位数回归旨在提供未来观测值的范围,在一定的置信度下。它估计自变量与因变量条件分布的不同量化值之间的关系。
其次,它们的计算方法不同:
- 在线性回归中,置信区间是对自变量系数的区间估计,通常使用普通最小二乘法 (OLS) 找出数据点到直线的最小总距离。系数的变化会影响预测的条件均值 Y。
- 在分位数回归中,你可以选择依赖变量的不同量级来估计回归系数,通常是最小化绝对偏差的加权和,而不是使用OLS方法。
第三,它们的应用不同:
- 在线性回归中,预测的条件均值有 95% 的置信区间。置信区间较窄,因为它是条件平均值,而不是整个范围。
- 在分位数回归中,预测值有 95% 的概率落在预测区间的范围内。
写在最后
本文介绍了分位数回归预测区间的概念,以及如何利用 NeuralProphet 生成预测区间。我们还强调了预测区间和置信区间之间的差异,这在商业应用中经常引起混淆。后面将继续探讨另一项重要的技术,即复合分位数回归(CQR),用于预测不确定性。
Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!

Outils d'IA chauds

Undresser.AI Undress
Application basée sur l'IA pour créer des photos de nu réalistes

AI Clothes Remover
Outil d'IA en ligne pour supprimer les vêtements des photos.

Undress AI Tool
Images de déshabillage gratuites

Clothoff.io
Dissolvant de vêtements AI

AI Hentai Generator
Générez AI Hentai gratuitement.

Article chaud

Outils chauds

Bloc-notes++7.3.1
Éditeur de code facile à utiliser et gratuit

SublimeText3 version chinoise
Version chinoise, très simple à utiliser

Envoyer Studio 13.0.1
Puissant environnement de développement intégré PHP

Dreamweaver CS6
Outils de développement Web visuel

SublimeText3 version Mac
Logiciel d'édition de code au niveau de Dieu (SublimeText3)
 Comment exécuter le projet H5
Apr 06, 2025 pm 12:21 PM
Comment exécuter le projet H5
Apr 06, 2025 pm 12:21 PM
L'exécution du projet H5 nécessite les étapes suivantes: Installation des outils nécessaires tels que le serveur Web, Node.js, les outils de développement, etc. Créez un environnement de développement, créez des dossiers de projet, initialisez les projets et écrivez du code. Démarrez le serveur de développement et exécutez la commande à l'aide de la ligne de commande. Aperçu du projet dans votre navigateur et entrez l'URL du serveur de développement. Publier des projets, optimiser le code, déployer des projets et configurer la configuration du serveur Web.
 La production de pages H5 nécessite-t-elle une maintenance continue?
Apr 05, 2025 pm 11:27 PM
La production de pages H5 nécessite-t-elle une maintenance continue?
Apr 05, 2025 pm 11:27 PM
La page H5 doit être maintenue en continu, en raison de facteurs tels que les vulnérabilités du code, la compatibilité des navigateurs, l'optimisation des performances, les mises à jour de sécurité et les améliorations de l'expérience utilisateur. Des méthodes de maintenance efficaces comprennent l'établissement d'un système de test complet, à l'aide d'outils de contrôle de version, de surveiller régulièrement les performances de la page, de collecter les commentaires des utilisateurs et de formuler des plans de maintenance.
 Pouvez-vous apprendre à faire des pages H5 par vous-même?
Apr 06, 2025 am 06:36 AM
Pouvez-vous apprendre à faire des pages H5 par vous-même?
Apr 06, 2025 am 06:36 AM
Il est possible de l'auto-étude de la production de pages H5, mais ce n'est pas un succès rapide. Il nécessite la maîtrise de HTML, CSS et JavaScript, impliquant la conception, le développement frontal et la logique d'interaction arrière. La pratique est la clé et apprenez en terminant des tutoriels, en examinant le matériel et en participant à des projets open source. L'optimisation des performances est également importante, nécessitant une optimisation des images, la réduction des demandes HTTP et l'utilisation de cadres appropriés. La route vers l'auto-apprentissage est longue et nécessite un apprentissage et une communication continus.
 Comment afficher les résultats après le bootstrap
Apr 07, 2025 am 10:03 AM
Comment afficher les résultats après le bootstrap
Apr 07, 2025 am 10:03 AM
Étapes pour afficher les résultats de bootstrap modifiés: ouvrez le fichier HTML directement dans le navigateur pour vous assurer que le fichier bootstrap est référencé correctement. Effacer le cache du navigateur (Ctrl Shift R). Si vous utilisez CDN, vous pouvez modifier directement CSS dans l'outil de développement pour afficher les effets en temps réel. Si vous modifiez le code source bootstrap, téléchargez et remplacez le fichier local ou réacheminez la commande build à l'aide d'un outil de build tel que WebPack.
 Comment utiliser la pagination Vue
Apr 08, 2025 am 06:45 AM
Comment utiliser la pagination Vue
Apr 08, 2025 am 06:45 AM
La pagination est une technologie qui divise de grands ensembles de données en petites pages pour améliorer les performances et l'expérience utilisateur. Dans Vue, vous pouvez utiliser la méthode intégrée suivante pour la pagination: Calculez le nombre total de pages: TotalPages () Numéro de page de traversée: Directive V-FOR pour définir la page actuelle: CurrentPage Obtenez les données de la page actuelle: CurrentPagedata ()
 HaDIDB: une base de données légère et évolutive horizontalement dans Python
Apr 08, 2025 pm 06:12 PM
HaDIDB: une base de données légère et évolutive horizontalement dans Python
Apr 08, 2025 pm 06:12 PM
HaDIDB: Une base de données Python évolutive de haut niveau légère HaDIDB (HaDIDB) est une base de données légère écrite en Python, avec un niveau élevé d'évolutivité. Installez HaDIDB à l'aide de l'installation PIP: PiPinStallHaDIDB User Management Créer un utilisateur: CreateUser () pour créer un nouvel utilisateur. La méthode Authentication () authentifie l'identité de l'utilisateur. FromHadidb.OperationMportUserUser_OBJ = User ("Admin", "Admin") User_OBJ.
 Surveillez les gouttelettes MySQL et MariaDB avec Exportateur de Prometheus Mysql
Apr 08, 2025 pm 02:42 PM
Surveillez les gouttelettes MySQL et MariaDB avec Exportateur de Prometheus Mysql
Apr 08, 2025 pm 02:42 PM
Une surveillance efficace des bases de données MySQL et MARIADB est essentielle pour maintenir des performances optimales, identifier les goulots d'étranglement potentiels et assurer la fiabilité globale du système. Prometheus Mysql Exportateur est un outil puissant qui fournit des informations détaillées sur les mesures de base de données qui sont essentielles pour la gestion et le dépannage proactifs.
 Comment afficher le comportement javascript de Bootstrap
Apr 07, 2025 am 10:33 AM
Comment afficher le comportement javascript de Bootstrap
Apr 07, 2025 am 10:33 AM
La section JavaScript de Bootstrap fournit des composants interactifs qui donnent une vitalité des pages statiques. En regardant le code open source, vous pouvez comprendre comment cela fonctionne: la liaison des événements déclenche les opérations DOM et les modifications de style. L'utilisation de base comprend l'introduction de fichiers JavaScript et l'utilisation d'API, et l'utilisation avancée implique des événements personnalisés et des capacités d'extension. Les questions fréquemment posées incluent les conflits de version et les conflits de style CSS, qui peuvent être résolus en vérifiant le code. Les conseils d'optimisation des performances incluent le chargement à la demande et la compression de code. La clé pour maîtriser Bootstrap JavaScript est de comprendre ses concepts de conception, de combiner des applications pratiques et d'utiliser des outils de développement pour déboguer et explorer.





