 interface Web
interface Web
 js tutoriel
js tutoriel
 Explication détaillée de l'arbre binaire des structures de données et des algorithmes JavaScript_Connaissances de base
Explication détaillée de l'arbre binaire des structures de données et des algorithmes JavaScript_Connaissances de base
Explication détaillée de l'arbre binaire des structures de données et des algorithmes JavaScript_Connaissances de base
Le concept d'arbre binaire
L'arbre binaire est un ensemble fini de n (n>=0) nœuds. L'ensemble est soit un ensemble vide (arbre binaire vide), soit il se compose d'un nœud racine et de deux arbres mutuellement disjoints. composé du sous-arbre gauche et du sous-arbre droit du nœud racine.

Caractéristiques des arbres binaires
Chaque nœud a au plus deux sous-arbres, il n'y a donc aucun nœud avec un degré supérieur à 2 dans l'arbre binaire. Chaque nœud de l'arborescence binaire est un objet et chaque nœud de données possède trois pointeurs, qui sont des pointeurs vers le parent, l'enfant de gauche et l'enfant de droite. Chaque nœud est connecté les uns aux autres via des pointeurs. La relation entre les pointeurs connectés est une relation parent-enfant.
Définition du nœud d'arbre binaire
Les nœuds de l'arbre binaire sont définis comme suit :
struct BinaryTreeNode
{
int m_nValue;
BinaryTreeNode* m_pLeft;
BinaryTreeNode* m_pRight;
};
Cinq formes de base d'arbres binaires
Arbre binaire vide
Il n'y a qu'un seul nœud racine
Le nœud racine n'a que le sous-arbre gauche
Le nœud racine n'a que le bon sous-arbre
Le nœud racine a des sous-arbres gauche et droit

Il n'y a que deux situations pour un arbre ordinaire à trois nœuds : deux couches ou trois couches. Mais comme l'arbre binaire doit distinguer la gauche et la droite, il évoluera vers les cinq formes suivantes :

Arbre binaire spécial
Arbre incliné
Comme le montrent les 2ème et 3ème images de la dernière photo ci-dessus.
Arbre binaire complet
Dans un arbre binaire, si tous les nœuds de branche ont des sous-arbres gauche et droit, et que toutes les feuilles sont au même niveau, un tel arbre binaire est appelé un arbre binaire complet. Comme indiqué ci-dessous :
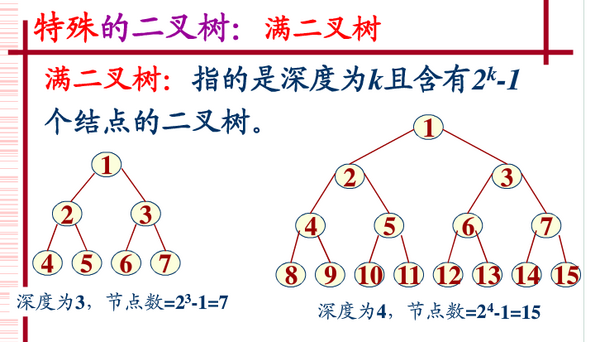
Arbre binaire complet
Un arbre binaire complet signifie que le côté gauche du dernier niveau est plein, le côté droit peut être plein ou non, puis les niveaux restants sont pleins. Un arbre binaire de profondeur k et de nombre de nœuds 2 ^ k - 1 est un arbre binaire complet (arbre binaire complet). C'est un arbre de profondeur k et sans trou.
Les caractéristiques d'un arbre binaire complet sont :
Les nœuds feuilles ne peuvent apparaître que sur les deux niveaux inférieurs.
Les feuilles les plus basses doivent être concentrées sur la position continue gauche.
Sur l'avant-dernière couche, s'il y a des nœuds feuilles, ils doivent être dans des positions continues à droite.
Si le degré du nœud est 1, alors le nœud n'a laissé qu'un enfant.
Un arbre binaire avec le même arbre de nœuds, un arbre binaire complet a la plus petite profondeur.
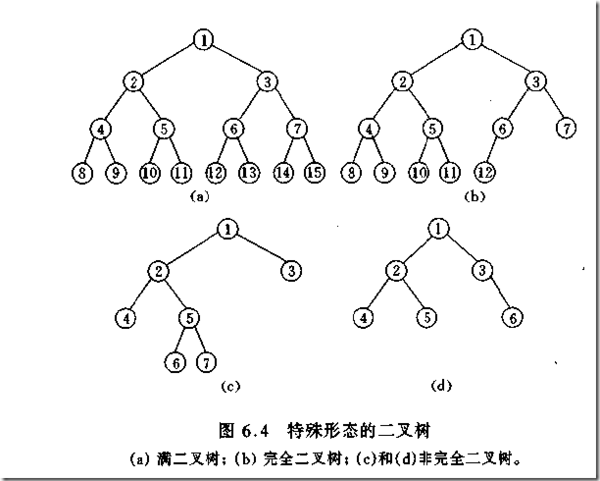
Remarque : un arbre binaire complet doit être un arbre binaire complet, mais un arbre binaire complet n'est pas nécessairement un arbre binaire complet.
L'algorithme est le suivant :
bool is_complete(arbre *racine)
{
file d'attente q
arbre *ptr
// Effectue un parcours en largeur (traversée de niveau) et met les nœuds NULL dans la file d'attente
q.push(racine);
Tandis que ((ptr = q.pop()) != NULL)
{
q.push(ptr->gauche); q.push(ptr->right); }
// Détermine s'il existe des nœuds non visités Tandis que (!q.is_empty())
{
ptr = q.pop();
// S'il y a des nœuds non NULL non visités, l'arbre a des trous et est un arbre binaire non complet
return false ;
}
renvoie vrai ;
}
Propriétés des arbres binaires
Propriété 1 d'un arbre binaire : Il y a au plus 2^(i-1) nœuds (i>=1) au i-ème niveau de l'arbre binaire
Propriété 2 des arbres binaires : Un arbre binaire de profondeur k a au plus 2^k-1 nœuds (k>=1)
Structure de stockage séquentielle de l'arbre binaire
La structure de stockage séquentielle d'un arbre binaire utilise un tableau unidimensionnel pour stocker chaque nœud dans l'arbre binaire, et l'emplacement de stockage des nœuds peut refléter la relation logique entre les nœuds.

Liste chaînée binaire
Étant donné que l'applicabilité du stockage séquentiel n'est pas forte, nous devons considérer la structure de stockage en chaîne. Selon la pratique internationale, le stockage des arbres binaires utilise généralement une structure de stockage en chaîne.
Chaque nœud d'un arbre binaire a au plus deux enfants, c'est donc une idée naturelle de concevoir un champ de données et deux champs de pointeur pour celui-ci. Nous appelons une telle liste chaînée une liste chaînée binaire.

Parcours d'arbre binaire
Parcourir un arbre binaire signifie partir du nœud racine et visiter tous les nœuds de l'arbre binaire dans un certain ordre afin que chaque nœud soit visité une et une seule fois.
Il existe trois façons de parcourir un arbre binaire, comme suit :
(1) Traversée de précommande (DLR), visitez d'abord le nœud racine, puis traversez le sous-arbre de gauche et enfin traversez le sous-arbre de droite. L'abréviation racine-gauche-droite.
(2) Le parcours dans l'ordre (LDR), traverse d'abord le sous-arbre de gauche, puis visite le nœud racine et traverse enfin le sous-arbre de droite. Abrégé en gauche-racine-droite.
(3) Le parcours post-ordre (LRD), traverse d'abord le sous-arbre gauche, puis traverse le sous-arbre droit et visite enfin le nœud racine. Abrégé en racine gauche-droite.
Parcours des précommandes :
Si l'arbre binaire est vide, aucune opération n'est renvoyée, sinon le nœud racine est visité en premier, puis le sous-arbre de gauche est parcouru en pré-ordre, puis le sous-arbre de droite est parcouru en pré-ordre.
L'ordre de parcours est : A B D H I E J C F K G
//Parcours des précommandes
fonction preOrder(nœud){
Si(!node == null){
putstr(node.show() " ");
preOrder(node.left);
preOrder(node.right);
>
>
Parcours dans l'ordre :
Si l'arbre est vide, aucune opération ne revient, sinon en partant du nœud racine (notez que le nœud racine n'est pas visité en premier), parcourez le sous-arbre gauche du nœud racine dans l'ordre, puis visitez le nœud racine, et enfin Parcourez le sous-arbre de droite dans l'ordre.

L'ordre de parcours est : H D I B E J A F K C G
//Utiliser la récursivité pour implémenter le parcours dans l'ordre
fonction dansOrdre(nœud){
Si(!(noeud == null)){
inOrder(node.left);//Visitez d'abord le sous-arbre de gauche
putstr(node.show() " ");//Visitez à nouveau le nœud racine
inOrder(node.right);//Dernier accès au sous-arbre de droite
>
>
Parcours post-commande :
Si l'arbre est vide, l'opération sans opération revient, sinon les sous-arbres gauche et droit sont parcourus de gauche à droite, d'abord les feuilles puis les nœuds, et enfin le nœud racine est visité.

L'ordre de parcours est : H I D J E B K F G C A
//Parcours post-commande
fonction postOrder(noeud){
Si(!node == null){
PostOrder(node.left);
postOrder(node.right);
putStr(node.show() " ");
>
>
Implémenter un arbre de recherche binaire
L'arbre de recherche binaire (BST) est composé de nœuds, nous définissons donc un objet nœud Node comme suit :
fonction Noeud (données, gauche, droite) {
This.data = data;
This.left = left;//Enregistrez le lien du nœud gauche
This.right = droite;
This.show = show;
>
fonction show(){
Renvoie this.data;//Affiche les données enregistrées dans le nœud
>
Trouver les valeurs maximales et minimales
Trouver les valeurs minimales et maximales sur un BST est très simple car la plus petite valeur est toujours sur le nœud enfant de gauche. Pour trouver la valeur minimale sur un BST, parcourez simplement le sous-arbre de gauche jusqu'à ce que le dernier nœud soit trouvé. 🎜>
Trouver la valeur minimale
var courant = this.root;
Tandis que(!(current.left == null)){
Actuel = actuel.gauche;
>
Renvoie current.data;
>
Trouver la valeur maximale
Trouver la valeur maximale sur BST nécessite uniquement de parcourir le sous-arbre droit jusqu'à ce que le dernier nœud soit trouvé, et la valeur enregistrée sur ce nœud est la valeur maximale.
var courant = this.root;
Tandis que(!(current.right == null)){
current = current.right;
>
Renvoie current.data;
>

Outils d'IA chauds

Undresser.AI Undress
Application basée sur l'IA pour créer des photos de nu réalistes

AI Clothes Remover
Outil d'IA en ligne pour supprimer les vêtements des photos.

Undress AI Tool
Images de déshabillage gratuites

Clothoff.io
Dissolvant de vêtements AI

AI Hentai Generator
Générez AI Hentai gratuitement.

Article chaud

Outils chauds

Bloc-notes++7.3.1
Éditeur de code facile à utiliser et gratuit

SublimeText3 version chinoise
Version chinoise, très simple à utiliser

Envoyer Studio 13.0.1
Puissant environnement de développement intégré PHP

Dreamweaver CS6
Outils de développement Web visuel

SublimeText3 version Mac
Logiciel d'édition de code au niveau de Dieu (SublimeText3)

Sujets chauds
 Implémentation d'algorithmes d'apprentissage automatique en C++ : défis et solutions courants
Jun 03, 2024 pm 01:25 PM
Implémentation d'algorithmes d'apprentissage automatique en C++ : défis et solutions courants
Jun 03, 2024 pm 01:25 PM
Les défis courants rencontrés par les algorithmes d'apprentissage automatique en C++ incluent la gestion de la mémoire, le multithread, l'optimisation des performances et la maintenabilité. Les solutions incluent l'utilisation de pointeurs intelligents, de bibliothèques de threads modernes, d'instructions SIMD et de bibliothèques tierces, ainsi que le respect des directives de style de codage et l'utilisation d'outils d'automatisation. Des cas pratiques montrent comment utiliser la bibliothèque Eigen pour implémenter des algorithmes de régression linéaire, gérer efficacement la mémoire et utiliser des opérations matricielles hautes performances.
 Explorez les principes sous-jacents et la sélection d'algorithmes de la fonction de tri C++
Apr 02, 2024 pm 05:36 PM
Explorez les principes sous-jacents et la sélection d'algorithmes de la fonction de tri C++
Apr 02, 2024 pm 05:36 PM
La couche inférieure de la fonction de tri C++ utilise le tri par fusion, sa complexité est O(nlogn) et propose différents choix d'algorithmes de tri, notamment le tri rapide, le tri par tas et le tri stable.
 Comparez des structures de données complexes à l'aide de la comparaison de fonctions Java
Apr 19, 2024 pm 10:24 PM
Comparez des structures de données complexes à l'aide de la comparaison de fonctions Java
Apr 19, 2024 pm 10:24 PM
Lors de l'utilisation de structures de données complexes en Java, Comparator est utilisé pour fournir un mécanisme de comparaison flexible. Les étapes spécifiques comprennent : la définition d’une classe de comparaison et la réécriture de la méthode de comparaison pour définir la logique de comparaison. Créez une instance de comparaison. Utilisez la méthode Collections.sort, en transmettant les instances de collection et de comparateur.
 Algorithme de détection amélioré : pour la détection de cibles dans des images de télédétection optique haute résolution
Jun 06, 2024 pm 12:33 PM
Algorithme de détection amélioré : pour la détection de cibles dans des images de télédétection optique haute résolution
Jun 06, 2024 pm 12:33 PM
01Aperçu des perspectives Actuellement, il est difficile d'atteindre un équilibre approprié entre efficacité de détection et résultats de détection. Nous avons développé un algorithme YOLOv5 amélioré pour la détection de cibles dans des images de télédétection optique haute résolution, en utilisant des pyramides de caractéristiques multicouches, des stratégies de têtes de détection multiples et des modules d'attention hybrides pour améliorer l'effet du réseau de détection de cibles dans les images de télédétection optique. Selon l'ensemble de données SIMD, le mAP du nouvel algorithme est 2,2 % meilleur que YOLOv5 et 8,48 % meilleur que YOLOX, permettant ainsi d'obtenir un meilleur équilibre entre les résultats de détection et la vitesse. 02 Contexte et motivation Avec le développement rapide de la technologie de télédétection, les images de télédétection optique à haute résolution ont été utilisées pour décrire de nombreux objets à la surface de la Terre, notamment des avions, des voitures, des bâtiments, etc. Détection d'objets dans l'interprétation d'images de télédétection
 Application d'algorithmes dans la construction de 58 plateformes de portraits
May 09, 2024 am 09:01 AM
Application d'algorithmes dans la construction de 58 plateformes de portraits
May 09, 2024 am 09:01 AM
1. Contexte de la construction de la plateforme 58 Portraits Tout d'abord, je voudrais partager avec vous le contexte de la construction de la plateforme 58 Portraits. 1. La pensée traditionnelle de la plate-forme de profilage traditionnelle ne suffit plus. La création d'une plate-forme de profilage des utilisateurs s'appuie sur des capacités de modélisation d'entrepôt de données pour intégrer les données de plusieurs secteurs d'activité afin de créer des portraits d'utilisateurs précis. Elle nécessite également l'exploration de données pour comprendre le comportement et les intérêts des utilisateurs. et besoins, et fournir des capacités côté algorithmes ; enfin, il doit également disposer de capacités de plate-forme de données pour stocker, interroger et partager efficacement les données de profil utilisateur et fournir des services de profil. La principale différence entre une plate-forme de profilage d'entreprise auto-construite et une plate-forme de profilage de middle-office est que la plate-forme de profilage auto-construite dessert un seul secteur d'activité et peut être personnalisée à la demande. La plate-forme de mid-office dessert plusieurs secteurs d'activité et est complexe ; modélisation et offre des fonctionnalités plus générales. 2.58 Portraits d'utilisateurs de l'arrière-plan de la construction du portrait sur la plate-forme médiane 58
 Structures de données et algorithmes Java : explication détaillée
May 08, 2024 pm 10:12 PM
Structures de données et algorithmes Java : explication détaillée
May 08, 2024 pm 10:12 PM
Les structures de données et les algorithmes sont à la base du développement Java. Cet article explore en profondeur les structures de données clés (telles que les tableaux, les listes chaînées, les arbres, etc.) et les algorithmes (tels que le tri, la recherche, les algorithmes graphiques, etc.) en Java. Ces structures sont illustrées par des exemples pratiques, notamment l'utilisation de tableaux pour stocker les scores, de listes chaînées pour gérer les listes de courses, de piles pour implémenter la récursion, de files d'attente pour synchroniser les threads, ainsi que d'arbres et de tables de hachage pour une recherche et une authentification rapides. Comprendre ces concepts vous permet d'écrire du code Java efficace et maintenable.
 Structure de données PHP : l'équilibre des arborescences AVL, maintenant une structure de données efficace et ordonnée
Jun 03, 2024 am 09:58 AM
Structure de données PHP : l'équilibre des arborescences AVL, maintenant une structure de données efficace et ordonnée
Jun 03, 2024 am 09:58 AM
L'arbre AVL est un arbre de recherche binaire équilibré qui garantit des opérations de données rapides et efficaces. Pour atteindre l'équilibre, il effectue des opérations de virage à gauche et à droite, en ajustant les sous-arbres qui violent l'équilibre. Les arbres AVL utilisent l'équilibrage de hauteur pour garantir que la hauteur de l'arbre est toujours petite par rapport au nombre de nœuds, réalisant ainsi des opérations de recherche de complexité temporelle logarithmique (O (logn)) et maintenant l'efficacité de la structure de données même sur de grands ensembles de données.
 Algorithme de recommandation d'actualités basé sur l'amélioration globale des graphiques
Apr 08, 2024 pm 09:16 PM
Algorithme de recommandation d'actualités basé sur l'amélioration globale des graphiques
Apr 08, 2024 pm 09:16 PM
Auteur | Évalué par Wang Hao | L'application Chonglou News est un moyen important pour les gens d'obtenir des sources d'informations dans leur vie quotidienne. Vers 2010, les applications d'information étrangères populaires comprenaient Zite et Flipboard, tandis que les applications d'information nationales populaires étaient principalement les quatre principaux portails. Avec la popularité des produits de recommandation d'actualités d'une nouvelle ère représentés par Toutiao, les applications d'actualités sont entrées dans une nouvelle ère. Quant aux entreprises technologiques, quelle qu'elles soient, tant qu'elles maîtrisent la technologie sophistiquée des algorithmes de recommandation d'actualités, elles auront fondamentalement l'initiative et la voix au niveau technique. Aujourd'hui, jetons un coup d'œil à un article du RecSys2023 Best Long Paper Nomination Award : GoingBeyondLocal:GlobalGraph-EnhancedP.





