10000 contenu connexe trouvé
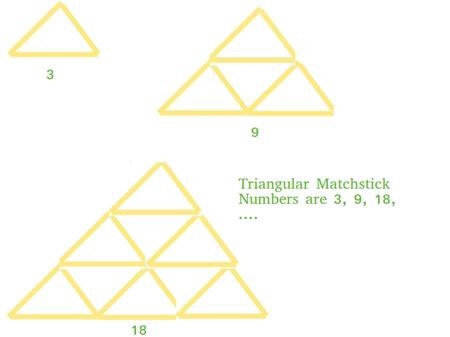
Programme C/C++ pour les nombres d'allumettes triangulaires ?
Présentation de l'article:Un triangle composé d'allumettes disposées pour former un triangle équilatéral est appelé un numéro de correspondance triangulaire. Le nombre de correspondances triangulaires est le nombre de correspondances nécessaires pour former un triangle de correspondances. Dans ce problème, notre nombre est la base X de la pyramide des correspondances. Notre tâche est d'écrire un programme qui imprime le nombre total d'allumettes requis pour former une pyramide d'allumettes de niveau X. Regardons un exemple pour rendre le concept plus clair, Input:7Output:84 explique qu'il s'agit d'une extension des nombres trigonométriques. Pour un entier X, le nombre d'allumettes requis sera trois fois le nombre de
2023-09-23
commentaire 0
1399

Trouver le nombre de paires possibles d'hypoténuses et d'aires d'un triangle rectangle en utilisant la programmation C++
Présentation de l'article:Dans cet article, nous expliquerons comment trouver le nombre de paires possibles d'hypoténuse et d'aire qui forment un triangle rectangle en C++. Nous devons déterminer le nombre de toutes les paires possibles d’une hypoténuse et d’une aire (H, A) formant un triangle rectangle, où H est l’hypoténuse et A est l’aire. Dans cet exemple - x = base du triangle rectangle y = hauteur du triangle rectangle H = hypoténuse du triangle rectangle On connaît l'aire du triangle rectangle, A=(x*y)/2 ou 4*A2=(x*y ) 2…(1)Nous savons aussi que x2+y2=H2…(2)Résoudre (1)&(2)4*A2=x2(H2-x2)Résoudre l'équation quadratique en x2 et laisser D ( Discriminant )>
2023-09-08
commentaire 0
1093

Comment créer 6 triangles en utilisant Java
Présentation de l'article:Pour imprimer six triangles en Java, vous devez d'abord savoir comment imprimer des triangles, tels que : contrôler le nombre de lignes dans la boucle for de premier niveau, contrôler le nombre d'espaces dans les boucles for de deuxième et troisième niveaux, et en contrôlant le nombre de *, vous pouvez alors imprimer les triangles. Ensuite, bouclez le triangle six fois de plus, vous obtenez donc six triangles.
2019-05-22
commentaire 0
3427

Nombre minimum de côtés nécessaires pour former un triangle
Présentation de l'article:Pour déterminer le nombre minimum de côtés requis pour former un triangle dans un graphique, nous avons analysé le réseau entre les centres. Un triangle peut être formé là où trois moyeux sont reliés exclusivement ou de manière détournée par des arêtes. Le nombre minimum d'arêtes requis est égal au nombre d'arêtes perdues dans les connexions existantes entre les trois hubs. En regardant le graphique et en distinguant les centres non liés, nous pouvons calculer le nombre de côtés supplémentaires nécessaires pour former le triangle. Cette méthode est différente car elle nécessite des ajustements minimes pour créer une relation triangulaire entre les centres du graphique. Méthodes utilisées Méthodes de parcours graphique Les méthodes de parcours graphique utilisées pour trouver le nombre minimum de côtés requis pour créer un triangle impliquent l'étude du graphique à l'aide de calculs de parcours tels que la recherche en profondeur d'abord (DFS) ou la recherche en largeur d'abord (BFS). de chaque graphique
2023-08-25
commentaire 0
929
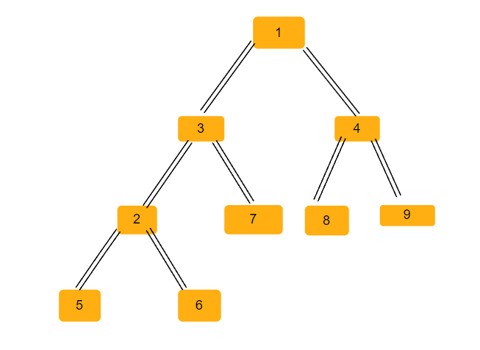
Le nombre de triangles isocèles dans un arbre binaire
Présentation de l'article:Un arbre binaire est une structure de données dans laquelle chaque nœud peut avoir jusqu'à deux nœuds enfants. Ces enfants sont appelés respectivement enfants de gauche et enfants de droite. Supposons que nous recevions une représentation de tableau parent, vous devez l'utiliser pour créer un arbre binaire. Un arbre binaire peut avoir plusieurs triangles isocèles. Nous devons trouver le nombre total de triangles isocèles possibles dans cet arbre binaire. Dans cet article, nous explorerons plusieurs techniques pour résoudre ce problème en C++. Comprendre le problème vous donne un tableau parent. Vous devez le représenter sous la forme d'un arbre binaire afin que l'index du tableau forme la valeur du nœud de l'arbre et que la valeur dans le tableau donne le nœud parent de cet index particulier. Notez que -1 est toujours le parent racine. Vous trouverez ci-dessous un tableau et sa représentation arborescente binaire. Tableau parental=[0,-1,3,1,
2023-09-05
commentaire 0
1096
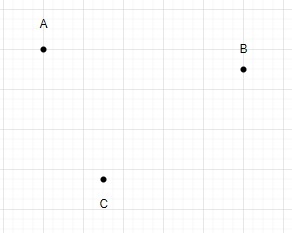
Si pas plus de deux points du plan sont colinéaires, quel est le nombre de triangles ?
Présentation de l'article:Voyons comment compter le nombre de triangles sur un plan étant donné n points et limiter le nombre de points colinéaires à deux maximum. Compter le nombre de triangles dans un plan ne comportant pas plus de deux points colinéaires est un problème typique de la géométrie computationnelle, qui a des applications en infographie, en traitement d'images et dans d'autres domaines de l'informatique. Par exemple, lors de la création d'une image 2D à partir d'une scène 3D dans des graphiques 3D, le problème du calcul de triangles dans un plan ne comportant pas plus de deux points colinéaires peut se poser. Dans ce cas, le processus de comptage de triangles peut être utilisé pour déterminer combien de triangles sont présents dans l’image 2D finale après projection de la scène 3D sur un plan. Cela vous permet de déterminer la complexité de la scène et d'augmenter la vitesse de rendu. En traitement d'image, nous pouvons vouloir compter le nombre d'objets ou de formes uniques dans une image. Ce problème est très complexe.
2023-09-05
commentaire 0
1274

Programme Java pour afficher le triangle de Floyd
Présentation de l'article:Le triangle de Floyd est un tableau triangulaire rectangle populaire de nombres naturels. Son nom vient de son fondateur, Robert W. Floyd, célèbre informaticien. Le haut du triangle est le chiffre 1, puis chaque chiffre suivant est incrémenté de 1 à mesure que vous descendez dans chaque ligne. Dans cet article, nous verrons comment afficher le triangle de Floyd à l'aide d'un programme Java. Mais avant de passer à l’implémentation Java, comprenons plus en profondeur le triangle de Freud. La première ligne contient un seul nombre, 1 lui-même, et chaque ligne suivante contient un nombre de plus que la ligne précédente. Un triangle comporte n lignes, où n peut être n’importe quel entier positif. Le nombre total de valeurs dans le triangle
2023-09-15
commentaire 0
1195

Comment réaliser le triangle isocèle de Yang Hui en PHP
Présentation de l'article:Le triangle isocèle de Yang Hui est l'une des figures classiques des mathématiques. Il a non seulement une belle apparence, mais possède également de bonnes propriétés mathématiques et est largement utilisé dans divers domaines. En programmation informatique, nous pouvons également utiliser divers langages pour implémenter l'algorithme de génération de triangle isocèle de Yang Hui. Cet article explique comment utiliser le langage PHP pour implémenter la génération de triangle isocèle de Yang Hui. 1. Le concept du triangle isocèle de Yang Hui Le triangle isocèle de Yang Hui est également appelé triangle de Pascal. C'est un triangle composé de nombres. Écrivez le chiffre 1 en haut du triangle, chaque chiffre est le deux. chiffres ci-dessus de et.
2023-04-24
commentaire 0
700

Le plus petit nombre trigonométrique supérieur à p
Présentation de l'article:Nous discuterons des nombres triangulaires et de la façon de trouver le plus petit nombre triangulaire qui est seulement supérieur au nombre donné « num ». Nous discuterons d'abord de ce qu'est un nombre trigonométrique, puis trouverons le plus petit nombre trigonométrique supérieur à "num". Nous verrons deux approches différentes du même problème. Dans la première méthode, nous exécuterons une boucle simple pour générer la sortie, tandis que dans la deuxième méthode, nous générerons d'abord une formule générale pour calculer le nombre requis, puis appliquerons directement cette formule pour obtenir le nombre minimum de Triangle. Énoncé du problème Nous devons trouver le plus petit nombre de triangles qui soit seulement supérieur à « num ». Nous avons plusieurs boîtes contenant des balles. Le nombre de balles que contient la boîte est un nombre triangulaire différent pour toutes les boîtes. Les cases sont numérotées de 1 à n. nous devons le découvrir à partir de la boîte
2023-09-20
commentaire 0
1272


Comment rendre les coins de contrôle d'un triangle transparents à l'aide de FabricJS ?
Présentation de l'article:Dans ce tutoriel, nous allons apprendre à rendre transparents les coins de contrôle d'un triangle à l'aide de FabricJS. Triangle est l'une des différentes formes fournies par FabricJS. Afin de créer un triangle, nous devons créer une instance de la classe Fabric.Triangle et l'ajouter au canevas. La propriété transparentCorners nous permet de rendre transparents les coins de contrôle du triangle. Syntaxe newFabric.Triangle({TransparentCorners:Boolean}:Object) Paramètres Options (facultatif) - Ce paramètre est un objet qui fournit une personnalisation supplémentaire à notre triangle. À l'aide de ce paramètre, vous pouvez modifier la relation entre transparentCorners et
2023-09-17
commentaire 0
1584

Quel est le plus grand triangle de Ruero inscrit dans un carré qui est un triangle rectangle ?
Présentation de l'article:Ici, nous verrons l'aire du plus grand triangle de Reuleaux inscrite dans un carré, qui à son tour est inscrit dans un triangle rectangle. La longueur du côté du carré est « a ». La hauteur d'un triangle de Reuleaux est x. La base du triangle est b, la hauteur est l et l'hypoténuse est h. Nous savons qu'un carré inscrit dans un triangle rectangle de hauteur l et de base b a une longueur de côté - la hauteur d'un triangle de Reuleaux est la même que a. Donc a=x. Par conséquent, l'aire d'un triangle de Reuleaux est - Exemple#include<iostream>#include<cmath>usingnamespacestd;fl
2023-09-04
commentaire 0
1556

Relation de conversion mutuelle des fonctions trigonométriques
Présentation de l'article:La relation de conversion entre les fonctions trigonométriques sec (sécante) est l'inverse de la valeur du sinus csc (cosécante) est l'inverse de la valeur du cosinus sin (sinus) le côté/hypoténuse opposé du triangle rectangle cos (cosinus) le membre/hypoténuse de le triangle rectangle Côté tan (tangente) le côté opposé/adjacent d'un triangle rectangle cot (cotangente) le côté adjacent/opposé d'un triangle rectangle et la formule des deux angles sin(A+B)=sinAcosB+cosAsinBsin(A-B)=sinAcosB -cosAsinBcos(A+ B)=cosAcosB-sinAsinBcos(AB)=cosAcosB+sinAsinBtan(A+B)=(tanA+tanB)/(1-tanAta
2024-01-15
commentaire 0
2724
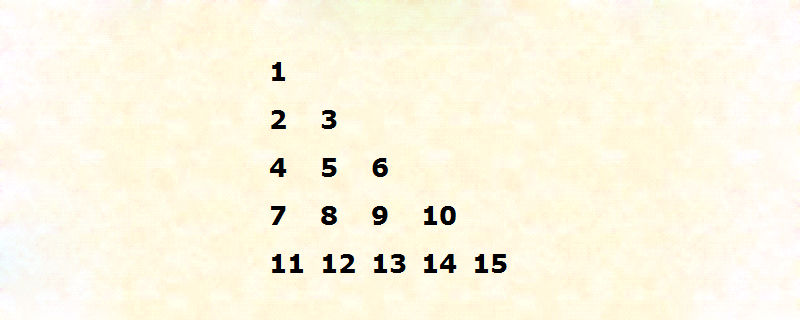
PHP implémente le triangle de Floyd
Présentation de l'article:Cet article explique comment utiliser PHP pour générer et afficher les n premières lignes du triangle de Floyd. (Utilisez les lignes n=5 et n=11) Le triangle de Freud est un ensemble de nombres naturels triangulaires rectangles utilisés dans l'enseignement de l'informatique. Il porte le nom de Robert Floyd. Il s'agit de remplir les lignes d'un triangle avec des nombres consécutifs, en commençant par la gauche.
2019-03-22
commentaire 0
3613

Comment implémenter des triangles en CSS
Présentation de l'article:Méthodes pour implémenter des triangles en CSS : 1. Utilisez des bordures pour implémenter des triangles. Utilisez une combinaison de bordures transparentes et de bordures solides pour créer des triangles dans différentes directions et tailles. 2. Utilisez des pseudo-éléments pour implémenter des triangles et utilisez des pseudo-éléments pour créer un parent ; élément qui occupe l'élément parent. Un triangle solide de la moitié de la taille ; 3. Utilisez l'attribut transform pour implémenter le triangle, et vous pouvez créer des triangles avec des angles différents en ajustant l'angle de rotation. 4. Utilisez l'attribut clip-path pour implémenter ; le triangle, et vous pouvez créer des triangles de formes différentes en définissant les coordonnées de plusieurs points.
2023-08-21
commentaire 0
3804