10000 contenu connexe trouvé
Arbres couvrant minimum
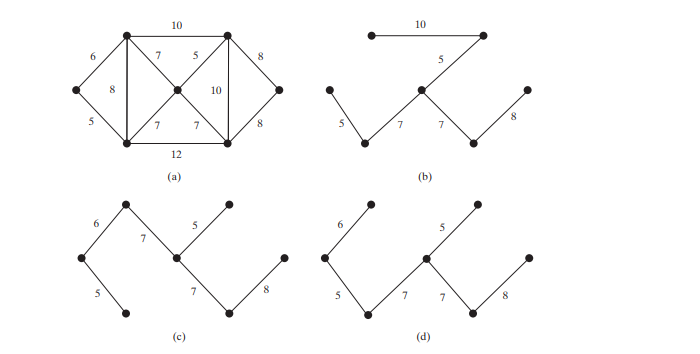
Présentation de l'article:Un arbre couvrant minimum d'un graphique est un arbre couvrant avec les poids totaux minimaux.
Un graphique peut avoir plusieurs arbres couvrants. Supposons que les bords soient pondérés. Un arbre couvrant minimum a les poids totaux minimum. Par exemple, les arbres des Figures
2024-09-06
commentaire 0
1189
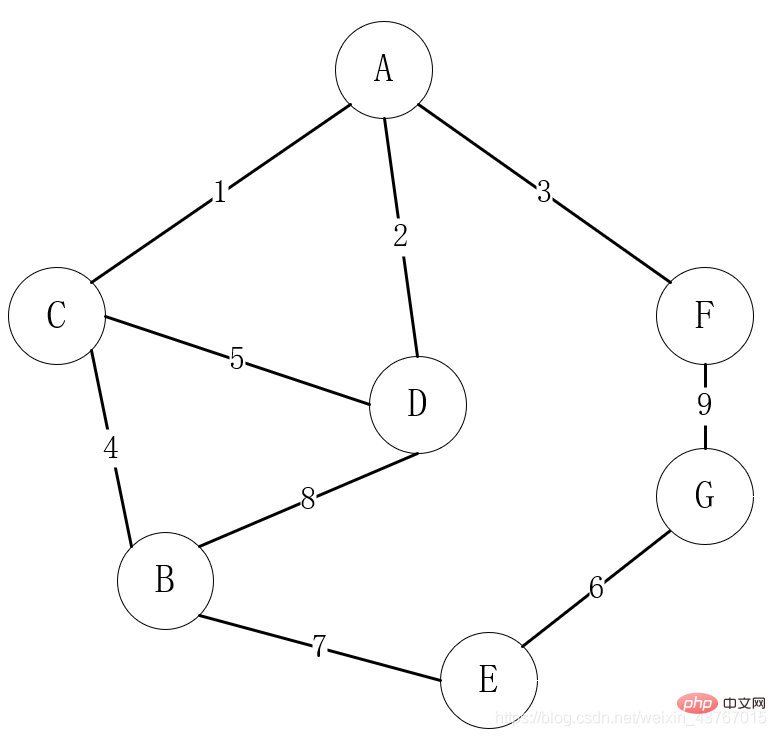
Comment trouver l'arbre couvrant minimum en Java
Présentation de l'article:1 Présentation de l'arbre couvrant minimum Spanning Tree (SpanningTree) : L'arbre couvrant d'un graphe connecté fait référence à un sous-graphe connecté, qui contient les n sommets du graphe, mais seulement n-1 arêtes suffisantes pour former un arbre. Un arbre couvrant avec n sommets n'a que n-1 arêtes. Si une autre arête est ajoutée à l'arbre couvrant, cela formera certainement un cycle. Arbre couvrant minimum (MinimumSpanningTree) : parmi tous les arbres couvrant d'un graphe connecté, le poids de toutes les arêtes et du plus petit arbre couvrant est appelé arbre couvrant minimum. Dans la vie, la structure graphique est la plus utilisée. Par exemple, dans la sélection d'itinéraires de construction d'un réseau de communication commun, les villages peuvent être considérés comme des sommets. S'il existe un chemin de communication entre les villages, il est compté comme un bord ou un arc entre deux points.
2023-04-29
commentaire 0
724

Explication détaillée de l'algorithme d'arbre couvrant minimum en PHP
Présentation de l'article:Une explication détaillée de l'algorithme du Spanning Tree minimum dans PHP Minimum Spanning Tree (MST en abrégé) est un concept important de la théorie des graphes, utilisé pour résoudre le problème de la sélection du bord de poids minimum d'un graphe connecté. Dans le langage PHP, nous pouvons implémenter cette fonction via certains algorithmes classiques de spanning tree minimum. Cet article présentera en détail deux algorithmes d'arbre couvrant minimum couramment utilisés : l'algorithme de Prim et l'algorithme de Kruskal, et donnera des exemples de code PHP correspondants. 1. Algorithme Prim L'algorithme Prim est un
2023-07-07
commentaire 0
1296

Explication détaillée d'exemples d'arbres couvrant minimum
Présentation de l'article:L'article est tiré de : Algorithme Spanning Tree-Prim minimum et algorithme Kruskal
L'arbre couvrant d'un graphe est son sous-graphe connecté acyclique contenant tous les sommets, et l'arbre couvrant minimum d'un graphe pondéré est son arbre couvrant avec le plus petit poids.
L'algorithme de Prim
Une brève description de l'algorithme
1).Entrée : un graphe connecté pondéré, dans lequel l'ensemble de sommets est V et l'ensemble d'arêtes est E ;
2).Initialisation : Vnew = {x}, où x est n'importe quel nœud (point de départ) dans l'ensemble V, Enew = {}, est vide ;
3). Répétez les opérations suivantes jusqu'à ce que Vnew
2017-06-25
commentaire 0
3461

Implémentation d'un arbre couvrant minimum en langage C
Présentation de l'article:L'arbre couvrant minimum (MST) consiste à trouver un arbre T dans un graphe non orienté donné G(V,E), tel que cet arbre ait tous les sommets du graphe G et que toutes les arêtes proviennent de Les arêtes du graphe G satisfont au poids minimum des arêtes somme de l’arbre entier.
2019-11-29
commentaire 0
3644

Comment implémenter l'algorithme d'arbre couvrant minimum à l'aide de Java
Présentation de l'article:Comment utiliser Java pour implémenter l'algorithme d'arbre couvrant minimum. L'algorithme d'arbre couvrant minimum est un problème classique de la théorie des graphes, qui est utilisé pour résoudre l'arbre couvrant minimum d'un graphe connecté pondéré. Cet article expliquera comment utiliser le langage Java pour implémenter cet algorithme et fournira des exemples de code spécifiques. Description du problème Étant donné un graphe connexe G, dans lequel chaque arête a un poids, il est nécessaire de trouver un arbre couvrant minimum T tel que la somme des poids de toutes les arêtes dans T soit minimale. L'algorithme de Prim L'algorithme de Prim est un algorithme glouton utilisé pour résoudre le problème de l'arbre couvrant minimum. son idée de base
2023-09-21
commentaire 0
1104

Comment écrire l'algorithme d'arbre couvrant minimum en utilisant C#
Présentation de l'article:Comment utiliser C# pour écrire l'algorithme d'arbre couvrant minimum L'algorithme d'arbre couvrant minimum est un algorithme important de la théorie des graphes, qui est utilisé pour résoudre le problème de connectivité des graphiques. En informatique, un arbre couvrant minimum fait référence à un arbre couvrant d'un graphe connecté dans lequel la somme des poids de toutes les arêtes de l'arbre couvrant est la plus petite. Cet article explique comment utiliser C# pour écrire l'algorithme d'arbre couvrant minimum et fournit des exemples de code spécifiques. Tout d’abord, nous devons définir une structure de données graphique pour représenter le problème. En C#, vous pouvez utiliser une matrice de contiguïté pour représenter un graphique. Une matrice de contiguïté est un tableau à deux dimensions dans lequel chaque élément représente
2023-09-19
commentaire 0
728

Algorithme d'arbre couvrant minimum de Kruskal - Algorithme gourmand en C++
Présentation de l'article:Un arbre couvrant est un sous-graphe d'un graphe orienté non orienté qui relie tous les sommets. Il peut y avoir plusieurs arbres couvrants dans un graphique. L'arbre couvrant minimum (MST) sur chaque graphique a un poids identique ou inférieur à celui de tous les autres arbres couvrant. Des poids sont attribués aux arêtes du spanning tree, et la somme correspond au poids attribué à chaque arête. Puisque V est le nombre de sommets dans le graphe, le nombre d’arêtes de l’arbre couvrant minimum est (V-1), où V est le nombre d’arêtes. Utilisez l'algorithme de Kruskal pour trouver l'arbre couvrant minimum. Toutes les arêtes doivent être disposées dans un ordre non décroissant par poids. Choisissez le plus petit côté. Si aucune boucle n'est formée, le bord est inclus. L'étape 2 doit être effectuée jusqu'à ce que l'arbre couvrant ait des bords (V-1). Dans ce cas, on nous dit d’utiliser l’approche gourmande. L’option gourmande est de choisir le bord avec le plus petit poids. Par exemple : l'arbre couvrant minimum de ce graphique est (9-1)=8
2023-08-28
commentaire 0
1206

Comment utiliser l'algorithme d'arbre couvrant minimum en C++
Présentation de l'article:Comment utiliser l'algorithme d'arbre couvrant minimum en C++. Le minimum Spanning Tree (MST) est un concept important dans la théorie des graphes. Il représente le sous-ensemble d'arêtes reliant tous les sommets d'un graphe connecté non orienté, et les poids de ces arêtes sont de et min. Il existe de nombreux algorithmes qui peuvent être utilisés pour résoudre l'arbre couvrant minimum, tels que l'algorithme de Prim et l'algorithme de Kruskal. Cet article présentera comment utiliser C++ pour implémenter l'algorithme de Prim et l'algorithme de Kruskal, et donnera des exemples de code spécifiques. L'algorithme de Prim est un
2023-09-20
commentaire 0
1262

Comment implémenter l'algorithme d'arbre couvrant minimum des graphiques à l'aide de Java
Présentation de l'article:Comment utiliser Java pour implémenter l'algorithme d'arbre couvrant minimum pour les graphiques Introduction au concept : L'arbre couvrant minimum (MST) fait référence à la recherche d'un arbre dans un graphe orienté pondéré ou un graphe non orienté de telle sorte qu'il contienne tous les sommets du graphe et la somme des poids. est le plus petit. Il existe de nombreux algorithmes d'arbre couvrant minimum, les deux algorithmes les plus classiques sont l'algorithme de Prim et l'algorithme de Kruskal. Algorithme de Prim : l'algorithme de Prim est un algorithme glouton basé sur des points qui part d'un sommet puis s'étend progressivement
2023-09-19
commentaire 0
1264

Algorithme Boruvka en C++ pour un arbre couvrant minimum
Présentation de l'article:En théorie des graphes, trouver l'arbre couvrant minimum (MST) d'un graphe pondéré connecté est un problème courant. MST est un sous-ensemble d'arêtes de graphique qui relie tous les sommets et minimise le poids total des arêtes. Un algorithme efficace pour résoudre ce problème est l’algorithme de Boruvka. Syntaxe structEdge{intsrc,dest,weight;};//Definethestructuretorepresentasubsetforunion-findstructSubset{intparent,rank;};Algorithme Maintenant, décrivons les étapes impliquées dans la recherche de l'arbre couvrant minimum dans l'algorithme de Boruvka - Initialiser le MST en tant qu'ensemble vide . pour chaque sommet
2023-08-27
commentaire 0
868

Comment résoudre le problème du spanning tree minimum en PHP en utilisant la méthode diviser pour régner et obtenir la solution optimale ?
Présentation de l'article:Comment résoudre le problème du spanning tree minimum en PHP en utilisant la méthode diviser pour régner et obtenir la solution optimale ? L'arbre couvrant minimum est un problème classique de la théorie des graphes, qui vise à trouver un sous-ensemble de tous les sommets d'un graphe connecté et à relier les arêtes de sorte que le sous-ensemble forme un arbre et que la somme des poids de toutes les arêtes soit la plus petite. La méthode diviser pour régner est une idée consistant à décomposer un gros problème en plusieurs sous-problèmes, puis à résoudre les sous-problèmes un par un et enfin à fusionner les résultats. L’utilisation de la méthode diviser pour régner pour résoudre le problème du spanning tree minimum en PHP peut être réalisée en suivant les étapes suivantes. Définissez la structure des données du graphique :
2023-09-19
commentaire 0
913

Comment utiliser un algorithme glouton pour obtenir la solution optimale du problème de l'arbre couvrant minimum en PHP ?
Présentation de l'article:Comment utiliser un algorithme glouton pour obtenir la solution optimale du problème de l'arbre couvrant minimum en PHP ? Le problème de l'arbre couvrant minimum (MinimumSpanningTree) consiste à trouver un sous-arbre dans un graphe non orienté connecté tel que ce sous-arbre contienne tous les sommets du graphe et que la somme des poids de toutes les arêtes soit la plus petite. L'algorithme glouton est l'une des méthodes courantes pour résoudre ce problème. Il trouve progressivement la solution optimale globale en sélectionnant à chaque fois la solution optimale actuelle. Tout d’abord, nous devons définir une classe de graphe pour stocker la structure du graphe et les poids des arêtes. Ce qui suit est un exemple de
2023-09-19
commentaire 0
1029

Pourquoi l'algorithme d'arbre couvrant minimum de Prim et Kruskal échoue-t-il dans les graphes orientés ?
Présentation de l'article:La méthode de Prim et l'algorithme de Kruskal sont deux méthodes courantes pour localiser le MST (minimum spanning tree) dans des graphiques non orientés. Cependant, ces techniques ne peuvent pas générer un MST correct pour les graphes orientés. En effet, les graphes orientés ne correspondent pas aux hypothèses et méthodes de base utilisées par les algorithmes de Prim et Kruskal. L'algorithme de Prim Tout d'abord, il y a l'algorithme de Prim, qui consiste à ajouter des arêtes à un arbre couvrant minimum en expansion de manière gourmande jusqu'à ce que tous les sommets soient couverts. Les sommets à l'intérieur du MST sont connectés aux sommets à l'extérieur du MST via l'arête ayant le poids le plus faible. Puisque toutes les arêtes d’un graphe non orienté peuvent se déplacer dans n’importe quelle direction, le chemin le plus court entre le MST et les sommets externes est facile à trouver. Cependant, dans un graphe orienté, les arêtes pointent toujours dans une direction et il peut ne pas y avoir de ligne droite.
2023-09-02
commentaire 0
658
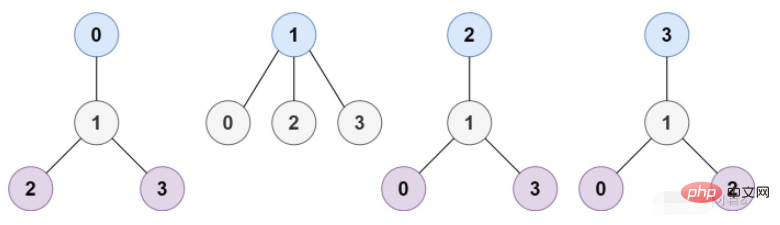
Comment implémenter un arbre de hauteur minimale en Java
Présentation de l'article:Le problème nécessite que l'arbre soit un graphe non orienté, dans lequel deux sommets quelconques sont reliés par un seul chemin. En d’autres termes, tout graphe connecté sans cycles simples est un arbre. Vous recevez un arbre contenant n nœuds, étiquetés de 0 à n-1. Étant donné un nombre n et une liste d'arêtes avec n-1 arêtes non orientées (chaque arête est une paire d'étiquettes), edge[i]=[ai,bi] signifie qu'il y a une arête entre les nœuds ai et bi dans l'arbre. bord. Vous pouvez choisir n’importe quel nœud de l’arborescence comme racine. Lors de la sélection du nœud x comme nœud racine, laissez la hauteur de l'arbre résultat être h. Parmi tous les arbres possibles, l’arbre ayant la hauteur minimale (c’est-à-dire min(h)) est appelé arbre de hauteur minimale. Veuillez trouver tous les arbres de hauteur minimale et retourner leur
2023-04-27
commentaire 0
762













