Cours Intermédiaire  11343

Introduction au cours："Tutoriel vidéo d'auto-apprentissage sur l'équilibrage de charge Linux du réseau informatique" implémente principalement l'équilibrage de charge Linux en effectuant des opérations de script sur le Web, lvs et Linux sous nagin.

Cours Avancé  17647

Introduction au cours："Tutoriel vidéo Shang Xuetang MySQL" vous présente le processus depuis l'installation jusqu'à l'utilisation de la base de données MySQL, et présente en détail les opérations spécifiques de chaque lien.

Cours Avancé  11354

Introduction au cours：« Tutoriel vidéo d'affichage d'exemples front-end de Brothers Band » présente des exemples de technologies HTML5 et CSS3 à tout le monde, afin que chacun puisse devenir plus compétent dans l'utilisation de HTML5 et CSS3.

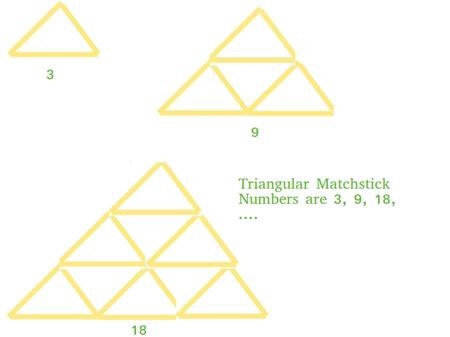
Introduction au cours：Un triangle composé d'allumettes disposées pour former un triangle équilatéral est appelé un numéro de correspondance triangulaire. Le nombre de correspondances triangulaires est le nombre de correspondances nécessaires pour former un triangle de correspondances. Dans ce problème, notre nombre est la base X de la pyramide des correspondances. Notre tâche est d'écrire un programme qui imprime le nombre total d'allumettes requis pour former une pyramide d'allumettes de niveau X. Regardons un exemple pour rendre le concept plus clair, Input:7Output:84 explique qu'il s'agit d'une extension des nombres trigonométriques. Pour un entier X, le nombre d'allumettes requis sera trois fois le nombre de

2023-09-23 commentaire 0  1410

Introduction au cours：Dans cet article, nous expliquerons comment trouver le nombre de paires possibles d'hypoténuse et d'aire qui forment un triangle rectangle en C++. Nous devons déterminer le nombre de toutes les paires possibles d’une hypoténuse et d’une aire (H, A) formant un triangle rectangle, où H est l’hypoténuse et A est l’aire. Dans cet exemple - x = base du triangle rectangle y = hauteur du triangle rectangle H = hypoténuse du triangle rectangle On connaît l'aire du triangle rectangle, A=(x*y)/2 ou 4*A2=(x*y ) 2​​…(1)Nous savons aussi que x2+y2=H2…(2)Résoudre (1)&(2)4*A2=x2(H2-x2)Résoudre l'équation quadratique en x2 et laisser D ( Discriminant )>

2023-09-08 commentaire 0  1110

Introduction au cours：Pour déterminer le nombre minimum de côtés requis pour former un triangle dans un graphique, nous avons analysé le réseau entre les centres. Un triangle peut être formé là où trois moyeux sont reliés exclusivement ou de manière détournée par des arêtes. Le nombre minimum d'arêtes requis est égal au nombre d'arêtes perdues dans les connexions existantes entre les trois hubs. En regardant le graphique et en distinguant les centres non liés, nous pouvons calculer le nombre de côtés supplémentaires nécessaires pour former le triangle. Cette méthode est différente car elle nécessite des ajustements minimes pour créer une relation triangulaire entre les centres du graphique. Méthodes utilisées Méthodes de parcours graphique Les méthodes de parcours graphique utilisées pour trouver le nombre minimum de côtés requis pour créer un triangle impliquent l'étude du graphique à l'aide de calculs de parcours tels que la recherche en profondeur d'abord (DFS) ou la recherche en largeur d'abord (BFS). de chaque graphique

2023-08-25 commentaire 0  939

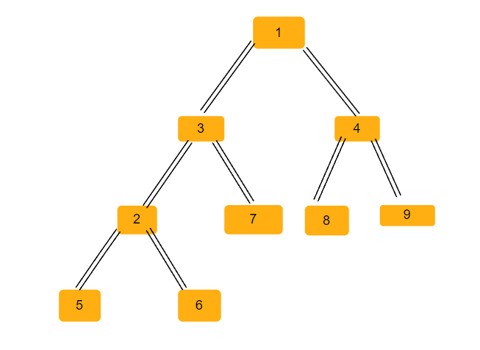
Introduction au cours：Un arbre binaire est une structure de données dans laquelle chaque nœud peut avoir jusqu'à deux nœuds enfants. Ces enfants sont appelés respectivement enfants de gauche et enfants de droite. Supposons que nous recevions une représentation de tableau parent, vous devez l'utiliser pour créer un arbre binaire. Un arbre binaire peut avoir plusieurs triangles isocèles. Nous devons trouver le nombre total de triangles isocèles possibles dans cet arbre binaire. Dans cet article, nous explorerons plusieurs techniques pour résoudre ce problème en C++. Comprendre le problème vous donne un tableau parent. Vous devez le représenter sous la forme d'un arbre binaire afin que l'index du tableau forme la valeur du nœud de l'arbre et que la valeur dans le tableau donne le nœud parent de cet index particulier. Notez que -1 est toujours le parent racine. Vous trouverez ci-dessous un tableau et sa représentation arborescente binaire. Tableau parental=[0,-1,3,1,

2023-09-05 commentaire 0  1104

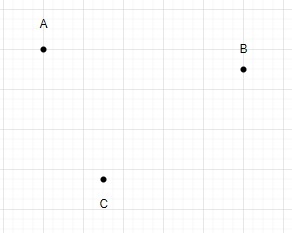
Introduction au cours：Voyons comment compter le nombre de triangles sur un plan étant donné n points et limiter le nombre de points colinéaires à deux maximum. Compter le nombre de triangles dans un plan ne comportant pas plus de deux points colinéaires est un problème typique de la géométrie computationnelle, qui a des applications en infographie, en traitement d'images et dans d'autres domaines de l'informatique. Par exemple, lors de la création d'une image 2D à partir d'une scène 3D dans des graphiques 3D, le problème du calcul de triangles dans un plan ne comportant pas plus de deux points colinéaires peut se poser. Dans ce cas, le processus de comptage de triangles peut être utilisé pour déterminer combien de triangles sont présents dans l’image 2D finale après projection de la scène 3D sur un plan. Cela vous permet de déterminer la complexité de la scène et d'augmenter la vitesse de rendu. En traitement d'image, nous pouvons vouloir compter le nombre d'objets ou de formes uniques dans une image. Ce problème est très complexe.

2023-09-05 commentaire 0  1286