javascript - Comment implémenter cet algorithme?

Question

Le format des données est le suivant : {code...} Description de la condition requise : Dessinez chaque donnée sur une carte de coordonnées d'un jour (00h00 - 24h00). Le diagramme schématique possible est le suivant : 1. Selon l'heure de début. et endTime des données, il peut être obtenu Obtenir les coordonnées des données sur l'axe Y (exprimées en valeurs de sommet et de hauteur, implémentées) 2....

PHP中文网 · Answer

Écrit en gros, l'idée de base est

Triez d'abord toutes les tâches de grande à petite (cette partie est omise)
Appuyez sur début et fin pour générer un objet tâche, et utilisez add_one de l'objet figure pour l'ajouter à la figure à son tour.
Lors de l'insertion d'un objet, déterminez les objets qui se chevauchent parmi les objets existants, rendez sa gauche égale à la gauche + 1 du plus grand objet qui se chevauche et mettez à jour la largeur maximale
Enfin, utilisez la méthode is_overlap pour détecter les événements dans les tâches qui ne croisent aucun événement et les marquer. La gauche de ces événements est définie sur 0 et la largeur est définie sur 100%. en dehors de ces événements, la largeur est définie sur 1/max_width, la gauche est définie sur 1/max_width*(left-1) (cette partie est omise)

Les codes suivants sont les étapes 2 et 3

function task(start, end) {
    var _this = this;
    this.start = start;
    this.end = end;
    this.left = 0;
    this.width = 0;
    this.is_overlap = function (t1, t2) {
        return !((t1 < _this.start && t2 < _this.start ) || (t1 > _this.end && t2 > _this.end));
    }
}

function figure() {
    var _this = this;
    this.tasks = [];
    this.max_width = 0;
    this.add_one = function (obj) {
        var overlap = [];
        var max_left = 0;
        for(var i = 0; i < _this.tasks.length; i++) {
            if (_this.tasks[i].is_overlap(obj.start, obj.end)){
                overlap.push(_this.tasks[i]);
            }
        }
        for(var i = 0; i < overlap.length; i++) {
            max_left = Math.max(overlap[i].left, max_left);
        }
        obj.left = max_left + 1;
        _this.max_width = Math.max(obj.left, _this.max_width);
        _this.tasks.push(obj);
    }
}

var fig = new figure();
var tasks = [];
tasks[0] = new task(3, 10);
tasks[1] = new task(8, 14);
tasks[2] = new task(5, 12);
tasks[3] = new task(2, 9);
tasks[4] = new task(18, 21);
// tasks[0] = new task(9, 15);
// tasks[1] = new task(0, 22);
// tasks[2] = new task(3, 7);
// tasks[3] = new task(9, 15);

for (var i = 0; i< tasks.length; i++){
    fig.add_one(tasks[i]);
}

for (var i = 0; i< fig.tasks.length; i++){
    console.log('index: '+ i +'  left: ' + fig.tasks[i].left);
}
console.log('width :'+fig.max_width);

某草草 · Answer

Regroupement 2D

Premier groupe verticalement (VGroups). Les événements qui ont des relations croisées sont regroupés dans le même groupe. Chaque groupe est indépendant (les groupes ne se croisent pas). L'algorithme de regroupement est le suivant : traitez chaque événement comme un nœud, et si deux nœuds se croisent, un bord est connecté. De cette façon, un graphe est obtenu, et le regroupement consiste à trouver les composantes connexes de ce graphe. Vous pouvez utiliser des algorithmes tels que la recherche en profondeur ou la recherche en largeur pour trouver des composants connectés. VGroups）。凡之间有相交关系的事件分入同一组。各组之间是独立的（组间不相交）。分组算法是：将每个事件看做节点，若两个节点相交，则连一条边。这样得到一个图，分组即求此图的连通分量。可以用深度优先搜索或者广度优先搜索等算法求连通分量。
纵向组内再横向分组（HGroups
Regroupez horizontalement au sein de groupes verticaux (HGroups). Les événements qui n'ont pas de relation

De cette façon, après avoir regroupé les deux dimensions verticalement et horizontalement, il est simple de les convertir en graphiques.

Test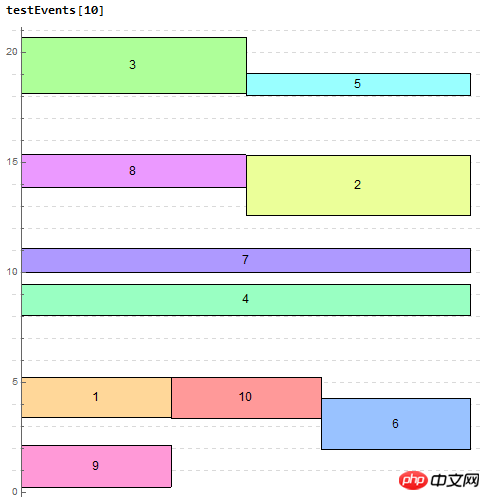

Ci-joint :

Mahematica🎜 code🎜

renderEvents[evts_List] := 
 Map[SortBy[-#duration &] /* renderVGroup]@
  ConnectedComponents@
   RelationGraph[{e1, e2} \[Function] 
     IntervalIntersection[e1["duration"], e2["duration"]] =!= 
      Interval[], evts]

renderVGroup[evts_List] := Module[{hgs, n},
  hgs = Last@
    NestWhile[{Rest@First@#, 
       addToGroups[Last@#, First@First@#]} &, {evts, {}}, 
     First[#] != {} &];
  n = Length[hgs];
  MapIndexed[renderHGroup[#1, (First[#2] - 1)/n, 1/n] &]@hgs]

addToGroups[gs_List, e_] := Module[{p},
  p = FirstPosition[gs,
    g_ /; 
     IntervalIntersection[IntervalUnion @@ (#duration & /@ g), 
       e["duration"]] === Interval[],
    Missing["NotFound"], {1}, Heads -> False];
  If[Head[p] === Missing,
   Append[gs, {e}],
   ReplacePart[gs, First[p] -> Append[gs[[First[p]]], e]]]]

renderHGroup[evts_List, x_, w_] :=
 Map[{#["color"], 
    Rectangle[{x, Min[#["duration"]]}, {x + w, Max[#["duration"]]}], 
    Black, Text[
     Style[#["title"], 
      Medium], {x + w/2, (Max[#["duration"]] + Min[#["duration"]])/
       2}]} &, evts]

testEvents[n_] := Module[{events},
  events = 
   Table[<|"title" -> ToString[i], 
     "duration" -> Interval[{#, # + #2}] &[RandomReal[{0, 21}], 
      RandomReal[{1, 3}]], "color" -> Hue[i/n, 0.4], 
     "order" -> i|>, {i, n}];
  Graphics[{EdgeForm[Thin], renderEvents[events]}, AspectRatio -> 1, 
   GridLines -> {None, Range[24]}, 
   GridLinesStyle -> {LightGray, Dashed}, Axes -> {None, True}]]

伊谢尔伦 · Answer

@saigyouyou
Ça pourrait être comme ça