Problèmes avec les types non signés et les types signés en C++

Question

Question 1 :
Comment comprenez-vous la phrase "Lorsque nous attribuons une valeur à un type non signé qui dépasse sa plage de représentation, le résultat est le reste de la valeur initiale modulo le nombre total de valeurs représentées par le type non signé" ? Par exemple, pourquoi le résultat de l'attribution de -1 à un caractère non signé de 8 bits est-il de 255 ?
Ma compréhension est la suivante : si -1=11111111 (le premier 1 représente négatif), lorsqu'il est exprimé comme non signé, 11111111=255
Alors pourquoi l'attribution d'un type signé donne-t-elle une valeur qui dépasse sa plage de représentation ?
Question 2
Lorsque les types signés et non signés apparaissent dans une expression arithmétique, lorsque la valeur du type signé est un nombre positif, la valeur après conversion en non signé est-elle la même qu'avant la conversion ? Par exemple, si int a=1, non signé b=1, lors de la sortie de a+b, a sera d'abord converti en non signé. Est-ce que a sera égal à 1 après la conversion ? Si int a=-1, non signé b=2, lors de la sortie de a+b, a sera d'abord converti en un type non signé. Quelle est la valeur de a après la conversion ?
Question 2 :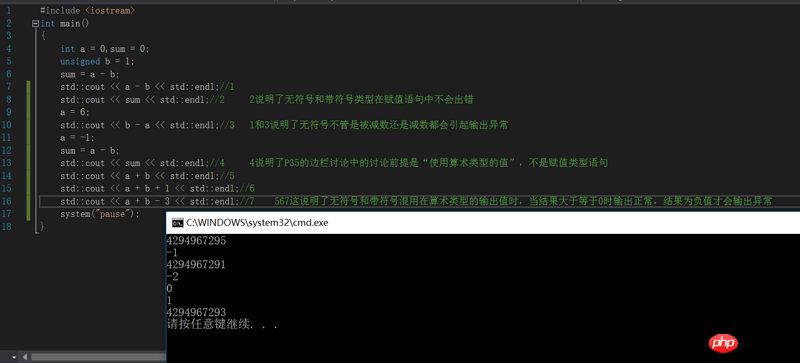

Comme le montre le quatrième long commentaire sur la photo.
Ce que dit le livre, c'est que quel que soit le résultat de a+b, tant que l'un de a et b n'est pas signé et que l'autre est signé, celui signé doit être converti en non signé avant d'effectuer l'addition. Après avoir exécuté le programme dans l'image, j'ai pensé que ce n'est que lorsque le résultat de a+b est un nombre négatif et que l'un de a et b est signé et l'autre non signé que le résultat sera converti en non signé.
Lequel a raison ?

Answer 1

Question 1
En fait, l'explication ci-dessus est compliquée. Si vous la regardez du point de vue de la mémoire, vous constaterez qu'elle est très simple. La différence entre non signé et signé n'est pas le stockage de la mémoire, mais l'acquisition de la mémoire. Par exemple, dans votre exemple d'attribution de -1 à 8 bits, s'il n'est pas signé, seuls les 8 derniers bits binaires seront remplis et le reste sera ignoré. Parce que ce 8 bits n'est pas signé, tous les bits binaires qu'il contient représentent des nombres, il s'agit donc de 255. Mais s'il s'agit d'un 8 bits signé, le premier binaire représente le bit de signe, mais lors de l'attribution, le bit de signe de -1 ne devient pas le bit de signe des données de 8 bits, donc le bit de signe du 8 bits les données ne sont en fait pas valides, donc cette affectation est Quelque chose s'est mal passé. Cette phrase signifie (-1)%256=255, où 256 est le nombre total (ou plage) de 8 bits non signés.
Question 2
Comme mentionné ci-dessus, en fait, les méthodes de stockage des signés et des non signés sont les mêmes, mais les méthodes de lecture sont différentes. Celui signé traitera le premier bit comme bit de signe, et celui non signé traitera le premier bit comme bit numérique. C'est la même chose en mémoire. Dans votre exemple, le résultat de la première fois a + b est un tas de 1 en représentation binaire. Si vous sortez directement, puisqu'il est converti en non signé, c'est-à-dire que deux non signés sont ajoutés, le résultat est non signé et la sortie binaire d'un groupe de 1 comme non signé est 4294967295, mais si a+b est affecté à somme, somme stocke la valeur. Il y a encore un tas de 1 dans la mémoire, mais comme sum est un entier signé, lors de la lecture, le premier bit est considéré comme le bit de signe, donc la valeur lue est -1.
Donc dans votre question 2, ce n'est pas qu'il n'y a pas de conversion pendant le fonctionnement, mais parce que seul le binaire est pris en compte lors du stockage des valeurs, et il n'y a aucune différence qu'il y ait un signe ou non. Le bit de signe n'est évalué qu'à la lecture, ce qui entraîne des différences dans les résultats de sortie.