Java - Vous cherchez une explication de l'algorithme suivant

Question

On sait que le tableau linéaire A de longueur n adopte une structure de stockage séquentielle. Veuillez écrire un algorithme avec une complexité temporelle de O(n) et une complexité spatiale de O(1). élément dans l’élément de tableau linéaire.

void  Delete（ElemType A[ ]，int  n）
∥A是有n个元素的一维数组，本算法删除A中所有值为item的元素。
{i=1；j=n；∥设置数组低、高端指针（下标）。
 while（i<j）
   {while（i<j && A[i]!=item）i++；         ∥若值不为item，左移指针。
    if（i<j）while（i<j && A[j]==item）j--；∥若右端元素为item，指针左移
    if（i<j）A[i++]=A[j--]；}

Il ne peut pas fonctionner après la réécriture. Voici celui réécrit

.

package 线性表;

public class Work_10 {
    public Work_10(){
        int[] arr={2,34,4,4,5};
        int item=4;
        delete(arr,item,arr.length-1);
        for(int a:arr){
            System.out.print(a+" ");
        }
    }
    public static void delete(int[] array,int item,int n){
        int i=0,j=n;
        while(i<j){
            while(i<j&&array[i]!=item) i++;
            if(i<j) while(i<j&&array[j]==item) j--;
            if(i<j){
                array[i++]=array[j--];
            }
        }
    }
    public static void main(String[] args) {
        new Work_10();
    }
}

Vous ne savez pas comment le changer ?
Veuillez expliquer, monsieur

Answer 1

Si vous souhaitez supprimer, recherchez d'abord, puis supprimez, je vous donnerai une recherche, et vous pourrez penser au reste et écrire une variante.

public static int search(byte[] a,int n, byte item) {
        int low = 0;
        int high = n - 1;

        while (low <= high) {
            int mid = (low + high) >>> 1;
            byte midVal = a[mid];

            if (midVal < item)
                low = mid + 1;
            else if (midVal > item)
                high = mid - 1;
            else
                return mid; // 找到item
        }
        return -(low + 1); // 没找到item
    }

Answer 2

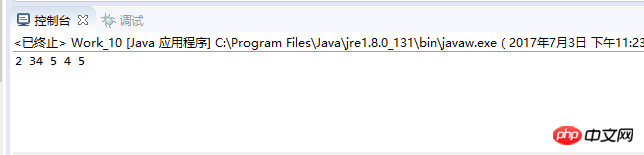
Oh, le numéro supplémentaire est dû au fait que le numéro que vous indiquez est erroné. Le processus de suppression se déroule bien.

Avant suppression, le contenu de votre tableau est 2,34,4,4,5, avec un total de 5 éléments.

Le contenu à supprimer est 4, ce qui signifie qu'il ne reste que 3 éléments après suppression, qui sont 2,34,5

Donc, votre résultat ne doit afficher que les 3 premiers éléments du tableau, et les deux derniers sont des éléments invalides.