
This article mainly introduces the relevant information on how to draw a polygon based on random points in canvas. The content is quite good. I will share it with you now and give it as a reference.
Cause
When I was studying the book "HTML5 Javascript Animation Basics" today, I talked about it in the third section of Chapter 8 How to use three springs to connect three points to perform a stretching exercise.
After finishing the example, I thought about what if it were four points or five points.
I rewrote the code and made the number of points variable. The final effect is to achieve the final stretching movement of each point to balance, but the connections between the points are not very good-looking, and some are crossed.
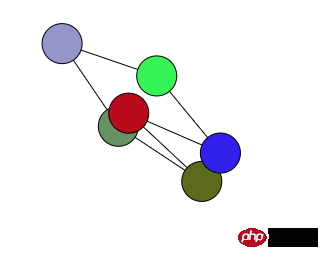
So I thought about whether I could optimize this area.
Rotating connection
The points in the previous example are all at random positions, so the connection is uncontrollable. So I want to start with this first.
First use a certain point as a reference point to obtain the angles of other points relative to this point.
Then connect these points according to the angle from small to large, so that you can draw a normal polygon.
The approximate implementation code is as follows:
let balls = [];
let ballNum = 6;
let firstBall = null;
while(ballNum--) {
let ball = new Ball(20, parseColor(Math.random() * 0xffffff))
ball.x = Math.random() * width;
ball.y = Math.random() * height;
balls.push(ball)
if (!firstBall) {
firstBall = ball
ball.angle = 0
} else {
const dx = ball.x - firstBall.x,
dy = ball.y - firstBall.y;
ball.angle = Math.atan2(dy, dx);
}
}
// 尝试让球连线是一个正多边形
balls = balls.sort((ballA, ballB) => {
return ballA.angle - ballB.angle
})In this way, when drawing the connection at the end, traversing the array can draw the angle from small to large. .
The effect is as follows:

This can greatly reduce the number of crossing lines, but it still cannot be completely avoided.
Next, I want to try to optimize this solution, such as using Math.abs to correct angle, or finding the point with the smallest angle to connect each point. But the result is no good, crossing lines cannot be avoided.
Rotation based on center point
Another idea came to mind later. If the center point of the polygon can be determined, then all points relative to the center are calculated separately. The angle between the points can be used to connect these points clockwise or counterclockwise.
But after searching for a long time on the Internet, all point algorithms require a series of points arranged in a certain clockwise order.
But if I have these points, I can already draw polygons. I had to give up
X-axis two-pole segmentation
In desperation, I had to search Google, and then I found an answer on Zhihu that was quite good. ’s: How to connect an unordered set of points on the plane into a simple polygon?
For the specific algorithm description, just look at the answer, I won’t go into details.
However, when connecting the upper chain and the lower chain, in fact, you only need to ensure that the upper chain is connected in descending order on the X axis, and the lower chain is connected in ascending order on the X axis (drawn in a counterclockwise direction). As for the points with the same X axis, it doesn't matter whether the Y axis is larger or smaller.
When implemented, it is implemented strictly according to the algorithm in the answer.
When judging whether a point belongs to the upper chain or the lower chain, the initial idea is to determine the function equation of the straight line based on two points, and then introduce the coordinates of the points for calculation. But later I thought that all points use the leftmost pole to calculate the oblique angle, and then divide it according to the angle size, which is easier to understand visually.
The approximate code is as follows:
let balls = [];
let tempBalls = [];
let ballNum = 6;
let isDragingBall = false;
while(ballNum--) {
let ball = new Ball(10, parseColor(Math.random() * 0xffffff))
ball.x = Math.random() * width;
ball.y = Math.random() * height;
tempBalls.push(ball)
}
// 让点按X轴升序排序
tempBalls = tempBalls.sort((ballA, ballB) => {
return ballA.x - ballB.x
})
// 找X轴左右极点
let firstBall = tempBalls[0],
lastBall = tempBalls[tempBalls.length -1];
let smallXBalls = tempBalls.filter(ball => ball.x === firstBall.x),
bigXBalls = tempBalls.filter(ball => ball.x === lastBall.x)
// 处理左右极点有多个的情况
if (smallXBalls.length > 1) {
smallXBalls.sort((ballA, ballB) => {
return ballB.y - ballA.y
})
}
if (bigXBalls.length > 1) {
bigXBalls.sort((ballA, ballB) => {
return ballB.y - ballA.y
})
}
firstBall = smallXBalls[0]
lastBall = bigXBalls[0]
// 获得极点连线的角度
let splitLineAngle = Math.atan2(lastBall.y - firstBall.y, lastBall.x - firstBall.x);
let upperBalls = [],
lowerBalls = [];
// 所有其他点跟firstBall计算角度
// 大于splitLineAngle的都是下链
// 其他是上链
tempBalls.forEach(ball => {
if (ball === firstBall || ball === lastBall) {
return false
}
let angle = Math.atan2(ball.y - firstBall.y, ball.x - firstBall.x);
if (angle > splitLineAngle) {
lowerBalls.push(ball)
} else {
upperBalls.push(ball)
}
})
// 处理X轴相同情况的排序
lowerBalls = lowerBalls.sort((ballA, ballB) => {
if (ballA.x !== ballB.x) {
return ballA.x - ballB.x
}
return ballB.y - ballA.y
})
upperBalls = upperBalls.sort((ballA, ballB) => {
if (ballA.x !== ballB.x) {
return ballB.x - ballA.x
}
return ballB.y - ballB.x
})
// 逆时针连接所有的点
balls = [firstBall].concat(lowerBalls, [lastBall], upperBalls)
balls = balls.map((ball, i) => {
ball.text = i + 1;
return ball
})The balls finally returned are the points of the polygon sorted counterclockwise.
The effect is as follows:
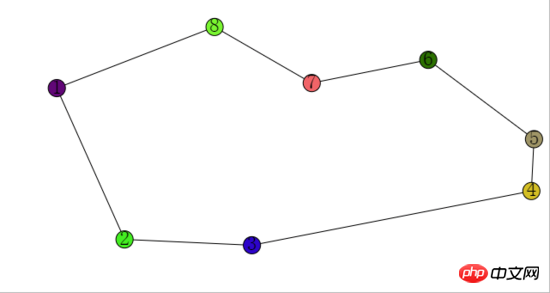
The internal state of each ball is as follows:

The above is the content of this article All content, I hope it will be helpful to everyone's learning. For more related content, please pay attention to the PHP Chinese website!
Related recommendations:
Use html5
Canvas encapsulates a pie chart that echarts cannot implement
HTML5 Canvas implements the method of drawing curves
The above is the detailed content of How to draw a polygon based on random points in canvas. For more information, please follow other related articles on the PHP Chinese website!
 What are the production methods of html5 animation production?
What are the production methods of html5 animation production?
 How to convert html to txt text format
How to convert html to txt text format
 modify ip
modify ip
 offsetwidth
offsetwidth
 Solution to the problem of downloading software and installing it in win11
Solution to the problem of downloading software and installing it in win11
 How to open two WeChat accounts on Huawei mobile phone
How to open two WeChat accounts on Huawei mobile phone
 oracle nvl
oracle nvl
 How to deduplicate database in mysql
How to deduplicate database in mysql




