
コードを作成するときに、四則演算式を自分で解析する必要がある状況に遭遇することがあります。この記事では、単純な四則演算式を解析するための JavaScript の使用方法を簡単に紹介します。
1. よく知られた概念
中置記法 (または中置記法) は、算術式または論理式を表現する一般的な方法です。演算子は中置形式のオペランドの真ん中にあります (例: 3 4)。つまり、最も一般的に使用される算術式である中置式は、人間にとっては理解しやすいですが、コンピューターにとっては解析が容易ではありません。
逆ポーランド記法 (逆ポーランド記法、RPN、または逆ポーランド記法) は、1920 年にポーランドの数学者 Jan Vukasiewicz によって導入された数式表現方法です。逆ポーランド記法では、すべての演算子がオペランドの後に配置されます。 , そのため、接尾辞表記とも呼ばれます。逆ポーランド記法では、演算子の優先順位を示す括弧は必要ありません。逆ポーランド記法を使用すると、スタック構造を使用して式を解析および計算することが容易になります。そのため、ここでは、最初に中置式を逆ポーランド式に変換することによって 4 つの要素式を解析します。次に、値を計算します。
2. 変換プロセス
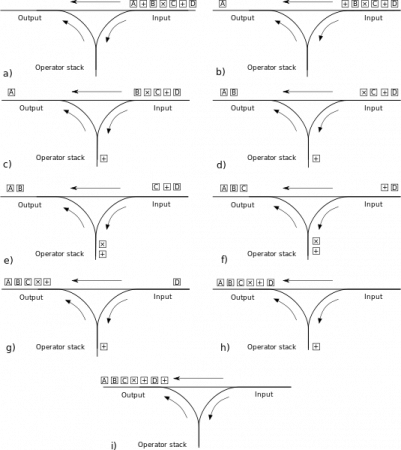
中置式を後置式に変換する (スケジュール フィールド アルゴリズム)
1. 入力キューにマークが表示されます
2. トークンが数値の場合、それを出力キューに追加します
3. 演算子 (-*/) の場合、出力スタックの先頭の演算子と比較し、優先順位がスタックの先頭の演算子以下の場合は、演算子を先頭にポップします。スタックの値を取得して出力キューに追加し (上記の条件が満たされなくなるまでループします)、最後にこの演算子をスタックにプッシュします。
4. 左括弧の場合は、スタックにプッシュします
5. 右括弧の場合は、スタックの先頭の要素が左括弧になるまで、継続的に演算子をスタックからポップし、出力キューに追加します。左括弧をポップし、出力キューに追加しないでください。左括弧が見つからない場合は、元の式の括弧が対称ではなく、エラーがあることを意味します。
6. 入力キューが空でスタックに演算子がまだある場合、スタックの先頭にある演算子が左括弧であれば、元の式に一致しない括弧があることを意味します。スタックから演算子を 1 つずつポップし、出力キューに追加します。
7.
を完了します
3. コード変換の実装
function isOperator(value){
var operatorString = "+-*/()";
return operatorString.indexOf(value) > -1
}
function getPrioraty(value){
switch(value){
case '+':
case '-':
return 1;
case '*':
case '/':
return 2;
default:
return 0;
}
}
function prioraty(o1, o2){
return getPrioraty(o1) <= getPrioraty(o2);
}
function dal2Rpn(exp){
var inputStack = [];
var outputStack = [];
var outputQueue = [];
for(var i = 0, len = exp.length; i < len; i++){
var cur = exp[i];
if(cur != ' ' ){
inputStack.push(cur);
}
}
console.log('step one');
while(inputStack.length > 0){
var cur = inputStack.shift();
if(isOperator(cur)){
if(cur == '('){
outputStack.push(cur);
}else if(cur == ')'){
var po = outputStack.pop();
while(po != '(' && outputStack.length > 0){
outputQueue.push(po);
po = outputStack.pop();
}
if(po != '('){
throw "error: unmatched ()";
}
}else{
while(prioraty(cur, outputStack[outputStack.length - 1]) && outputStack.length > 0){
outputQueue.push(outputStack.pop());
}
outputStack.push(cur);
}
}else{
outputQueue.push(new Number(cur));
}
}
console.log('step two');
if(outputStack.length > 0){
if(outputStack[outputStack.length - 1] == ')' || outputStack[outputStack.length - 1] == '('){
throw "error: unmatched ()";
}
while(outputStack.length > 0){
outputQueue.push(outputStack.pop());
}
}
console.log('step three');
return outputQueue;
}
console.log(dal2Rpn('1 + 2'));
console.log(dal2Rpn('1 + 2 + 3'));
console.log(dal2Rpn('1 + 2 * 3'));
console.log(dal2Rpn('1 + 2 * 3 - 4 / 5'));
console.log(dal2Rpn('( 1 + 2 )'));
console.log(dal2Rpn('( 1 + 2 ) * ( 3 - 4 ) / 5'));
console.log(dal2Rpn('( 1 + 2 ) * (( 3 - 4 ) / 5)'));4. 逆ポーランド語表現の評価
1. 入力キューからトークンをポップします
2. オペランドの場合は、出力スタックに追加します
3. 演算子の場合は、出力スタックから 2 つのオペランドをポップして計算を実行し、計算された値を出力スタックにプッシュします。
4. ループ操作。入力キューが空で、出力スタックに数値が 1 つだけある場合、この数値が結果になります。そうでない場合は、冗長オペランドが存在します。
5. 計算コード
function evalRpn(rpnQueue){
var outputStack = [];
while(rpnQueue.length > 0){
var cur = rpnQueue.shift();
if(!isOperator(cur)){
outputStack.push(cur);
}else{
if(outputStack.length < 2){
throw "unvalid stack length";
}
var sec = outputStack.pop();
var fir = outputStack.pop();
outputStack.push(getResult(fir, sec, cur));
}
}
if(outputStack.length != 1){
throw "unvalid expression";
}else{
return outputStack[0];
}
}
6.結論
逆ポーランド記法は、初めて触れたときは慣れないものですが、慣れてくると、さまざまな優先順位や優先順位がある中置記法とは異なり、その考え方が実際には非常に単純であることがわかります。括弧クラスのロジックは特に面倒ですが、逆ポーランド語表記の方が簡潔で、優先順位をまったく考慮する必要がなく、状況を混乱させる括弧、角括弧、中括弧も必要ありません。