
前の記事では、二分木の再帰的走査アルゴリズムについて説明しました (二分木のルート優先 (事前順序) 走査の改良) この記事では主に非再帰について説明します。スタック構造を使用した二分木のアルゴリズム
ルートトラバーサルによって得られた非再帰アルゴリズムのアイデアは次のように要約されます:
1) スタックにプッシュします。主に最初にヘッド ノードをスタックにプッシュし、次にこのノードにアクセスします
2) 一方、左側の子にノードがなくなるまで現在のノードをループします
3) ノードの右側の子が true の場合は 1) に進み、トラバースを続行します。それ以外の場合は、現在のノードを終了して親ノードに移動し、1) に進みます。
まず、このアイデアに準拠したアルゴリズムを見てみましょう:
BiTNode *pBiNode = T;
SqStack S;
InitStack(&S);
Push(&S, (SElemType)T);
while (!IsStackEmpty(S))
{
while (pBiNode)
{
VisitNode(pBiNode->data);
if (pBiNode != T)
{
Push(&S, (SElemType)pBiNode);
} > Pop(&S, (SElemType*)&pBiNode)
}
if (pBiNode->rchild == NULL); 🎜> {
Pop(&S, (SElemType*)&pBiNode); // この時点でスタックが空の場合は問題があります
}
pBiNode = pBiNode->rchild;
}
return 0;
}
シーケンシャル構造で保存されたスタック
を参照してください。
コードをコピー
コードは次のとおりです。
GetTop(S, (SElemType*)&pBiNode);
while (pBiNode)
{
VisitNode(pBiNode->data );
Push (&S, (SElemType)pBiNode) , (SElemType*)&pBiNode);
}
if ( !IsStackEmpty(S)); 🎜> {
Pop(&S, (SElemType*)&pBiNode);
pBiNode = pBiNode-> rchild;
Push(&S, (SElemType)pBiNode);
}
}
0 を返す;
}
これは次のようになります。最初にルート ノードをプッシュし、次に左側のサブツリーが空かどうかを判断し、空でない場合はスタックにプッシュします。そうでない場合は、while ループを終了した後、NULL ノードをポップします。スタックを調べ、現在のスタックが空かどうかを判断します。空でない場合は、スタックをポップして親ノードを取得します。次に、右側の子を判断し、右側の子ノードをプッシュして、右側の左側の子かどうかを判断します。サブツリーは空なので、ループを続行します。
ここには 2 つの無駄な場所があります。1 つは空の子ノードをスタックにプッシュすること、もう 1 つは GetTop を頻繁に使用してスタックの最上位要素を取得することです
ここで、最初に設計したアルゴリズムに戻りますが、たまたま NULL ポインターや空の子ノードがプッシュされていませんが、出力は完了していません。ここでは、スタックを判断するときにそれを追加することを考えます。現時点では、次のように、左側のサブツリー ノードが表示されず、右側のサブツリー ノードが表示されないという問題が発生しないように、ノードが NULL であっても問題ありません。
SqStack S;
InitStack(&S);
Push(&S, (SElemType)T);
{
while (pBiNode)
{
VisitNode(pBiNode->data);
if (pBiNode != T)
{
Push(&S, (SElemType)pBiNode);
}
pBiNode = pBiNode->lchild;
}
if( pBiNode == NULL)
{
Pop(&S, (SElemType*)&pBiNode);
}
if ( pBiNode->rchild == NULL)
{
Pop( &S, (SElemType*)&pBiNode); //この時点でスタックが空の場合は問題があります
}
pBiNode = pBiNode->rchild;
}
return 0;
}
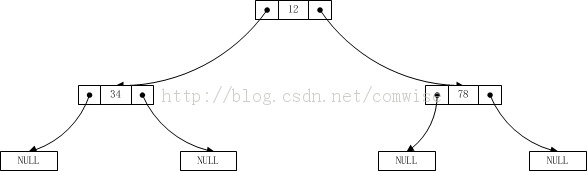
--- BiTree ---
BiTree ノード データを入力してください:
12
BiTree ノード データを入力してください:
34
BiTree ノード データを入力してください:
0
BiTree ノード データを入力してください:
0
BiTree ノード データを入力してください:
78
BiTree ノード データを入力してください:
0
BiTree ノード データを入力してください:
0
12 34 78
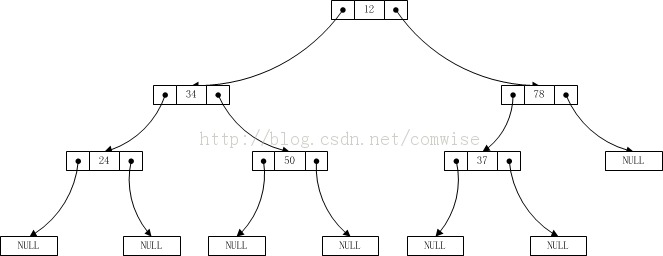
--- BiTree ---
BiTree ノード データを入力してください:
12
BiTree ノード データを入力してください:
34
BiTree ノード データを入力してください:
24
BiTree ノード データを入力してください:
0
BiTree ノード データを入力してください:
0
BiTree ノード データを入力してください:
50
BiTree ノード データを入力してください:
0
BiTree ノード データを入力してください:
0
BiTree ノード データを入力してください:
78
BiTree ノード データを入力してください:
37
BiTree ノード データを入力してください:
0
BiTree ノード データを入力してください:
0
BiTree ノード データを入力してください:
0
12 34 24 50 78 37