Thinkphp的list_to_tree 实现无限级分类列出所有节点
Thinkphp的list_to_tree 实现无限级分类列出所有节点
list_to_tree 使用起来十分方便,详细可查看手册。因为我在用的时候需要同时列出所有节点,所以写了一个递归函数,拿出来供大家参考。public function index(){
Load('extend'); //加载扩展方法
$Category=D('Category');
$list=$Category->order('sort desc')->select();//实现同级节点排序
$list=list_to_tree($list,'id','fid'); //详细参数见手册
$list=$this->findChild($list);
dump($list);
}
protected function findChild($arr){
static $tree=array();
foreach ($arr as $key=>$val){
$tree[]=$val;
if (isset($val['_child'])){
$this->findChild($val['_child']);
}
}
return $tree;
}/**
* 把返回的数据集转换成Tree
* @access public
* @param array $list 要转换的数据集
* @param string $pid parent标记字段
* @param string $level level标记字段
* @return array
*/
function list_to_tree($list, $pk='id',$pid = 'pid',$child = '_child',$root=0) {
// 创建Tree
$tree = array();
if(is_array($list)) {
// 创建基于主键的数组引用
$refer = array();
foreach ($list as $key => $data) {
$refer[$data[$pk]] =& $list[$key];
}
foreach ($list as $key => $data) {
// 判断是否存在parent
$parentId = $data[$pid];
if ($root == $parentId) {
$tree[] =& $list[$key];
}else{
if (isset($refer[$parentId])) {
$parent =& $refer[$parentId];
$parent[$child][] =& $list[$key];
}
}
}
}
return $tree;
}
/**
* 对查询结果集进行排序
* @access public
* @param array $list 查询结果
* @param string $field 排序的字段名
* @param array $sortby 排序类型
* asc正向排序 desc逆向排序 nat自然排序
* @return array
*/
function list_sort_by($list,$field, $sortby='asc') {
if(is_array($list)){
$refer = $resultSet = array();
foreach ($list as $i => $data)
$refer[$i] = &$data[$field];
switch ($sortby) {
case 'asc': // 正向排序
asort($refer);
break;
case 'desc':// 逆向排序
arsort($refer);
break;
case 'nat': // 自然排序
natcasesort($refer);
break;
}
foreach ( $refer as $key=> $val)
$resultSet[] = &$list[$key];
return $resultSet;
}
return false;
}
/**
* 在数据列表中搜索
* @access public
* @param array $list 数据列表
* @param mixed $condition 查询条件
* 支持 array('name'=>$value) 或者 name=$value
* @return array
*/
function list_search($list,$condition) {
if(is_string($condition))
parse_str($condition,$condition);
// 返回的结果集合
$resultSet = array();
foreach ($list as $key=>$data){
$find = false;
foreach ($condition as $field=>$value){
if(isset($data[$field])) {
if(0 === strpos($value,'/')) {
$find = preg_match($value,$data[$field]);
}elseif($data[$field]==$value){
$find = true;
}
}
}
if($find)
$resultSet[] = &$list[$key];
}
return $resultSet;
}

ホットAIツール

Undresser.AI Undress
リアルなヌード写真を作成する AI 搭載アプリ

AI Clothes Remover
写真から衣服を削除するオンライン AI ツール。

Undress AI Tool
脱衣画像を無料で

Clothoff.io
AI衣類リムーバー

AI Hentai Generator
AIヘンタイを無料で生成します。

人気の記事

ホットツール

メモ帳++7.3.1
使いやすく無料のコードエディター

SublimeText3 中国語版
中国語版、とても使いやすい

ゼンドスタジオ 13.0.1
強力な PHP 統合開発環境

ドリームウィーバー CS6
ビジュアル Web 開発ツール

SublimeText3 Mac版
神レベルのコード編集ソフト(SublimeText3)

ホットトピック
 7464
7464
 15
15
 1376
1376
 52
52
 77
77
 11
11
 18
18
 19
19
 ノード X から始まるサブツリーの最小重みと最大 D の距離を照会します。
Aug 25, 2023 am 11:25 AM
ノード X から始まるサブツリーの最小重みと最大 D の距離を照会します。
Aug 25, 2023 am 11:25 AM
コンピューター プログラミングを行う場合、特定のノードから D 単位以上離れたノードをサブツリーに含めることができないという条件で、特定のノードに由来するサブツリーの最小重みを見つけることが必要になる場合があります。この問題は、グラフ理論、ツリーベースのアルゴリズム、ネットワーク最適化など、さまざまな分野やアプリケーションで発生します。サブツリーは、指定されたノードがサブツリーのルート ノードとして機能する、より大きなツリー構造のサブセットです。サブツリーには、ルート ノードのすべての子孫とそれらの接続エッジが含まれます。ノードの重みは、そのノードに割り当てられた特定の値を指し、その重要性、重要性、またはその他の関連するメトリックを表すことができます。この問題の目標は、ルート ノードから最大 D 単位離れたノードにサブツリーを制限しながら、サブツリー内のすべてのノード間の最小重みを見つけることです。次の記事では、サブツリーから最小重みをマイニングする複雑さについて詳しく説明します。
 Vue と jsmind を使用してマインド マップのノード コピーおよびカット機能を実装するにはどうすればよいですか?
Aug 15, 2023 pm 05:57 PM
Vue と jsmind を使用してマインド マップのノード コピーおよびカット機能を実装するにはどうすればよいですか?
Aug 15, 2023 pm 05:57 PM
Vue と jsmind を使用してマインド マップのノード コピーおよびカット機能を実装するにはどうすればよいですか?マインド マップは、考えを整理し、思考ロジックを整理するのに役立つ一般的な思考ツールです。ノードのコピーとカット機能は、マインド マップでよく使用される操作であり、既存のノードをより便利に再利用し、思考整理の効率を向上させることができます。この記事では、Vue と jsmind の 2 つのツールを使用して、マインド マップのノードのコピーとカット機能を実装します。まず、Vue と jsmind をインストールし、
 jsでノードを削除する方法は何ですか
Sep 01, 2023 pm 05:00 PM
jsでノードを削除する方法は何ですか
Sep 01, 2023 pm 05:00 PM
js でノードを削除するメソッドは次のとおりです: 1. RemoveChild() メソッドは、指定された子ノードを親ノードから削除するために使用されます。これには 2 つのパラメータが必要です。最初のパラメータは削除される子ノードで、2 番目のパラメータは次のとおりです。親ノード ノード; 2.parentNode.removeChild() メソッドは、親ノードを介して直接呼び出して子ノードを削除できます; 3.remove() メソッドは、親ノードを指定せずにノードを直接削除できます; 4. innerHTML 属性は、ノードのコンテンツを削除するために使用されます。
 Floyd-Warshal アルゴリズムを使用して、任意の 2 つのノード間の最短パスを検索します。
Sep 20, 2023 pm 02:21 PM
Floyd-Warshal アルゴリズムを使用して、任意の 2 つのノード間の最短パスを検索します。
Sep 20, 2023 pm 02:21 PM
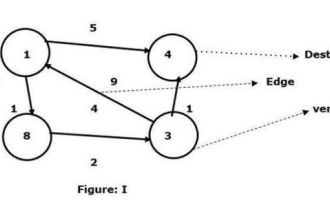
C++ にはコードの一部または期待値として定義されるマクロがあり、ユーザーが必要とするたびに再利用されます。フロイド・ウォルシャル アルゴリズムは、指定された重み付きグラフ内の頂点のすべてのペア間の最短経路を見つけるプロセスです。このアルゴリズムは動的プログラミング アプローチに従って、最小重みグラフを見つけます。図を通してフロイド・ウォルシャルアルゴリズムの意味を理解しましょう - 頂点 1 をソースとして、頂点 4 を目的地として取り、それらの間の最短パスを見つけます。ターゲット頂点 4 に接続できるパスが 2 つあることがわかりました。 1->4 – エッジの重みは 51->8->3->4 – エッジの重み (1+2+1)は4です。与えられたグラフ I では、2 つの頂点を接続する最小のエッジが表示されます。ここに頂点があります
 js で要素ノードを作成、削除、追加、置換する方法 (コード例付き)
Aug 06, 2022 pm 05:26 PM
js で要素ノードを作成、削除、追加、置換する方法 (コード例付き)
Aug 06, 2022 pm 05:26 PM
この記事では主にjsで要素ノードを作成、削除、追加、置換する方法を紹介しますので、困っている方の参考になれば幸いです。
 指定されたグラフ内の 2 つのノード間のパスが最短パスを表すかどうかを確認します
Sep 07, 2023 pm 06:57 PM
指定されたグラフ内の 2 つのノード間のパスが最短パスを表すかどうかを確認します
Sep 07, 2023 pm 06:57 PM
グラフの 2 つの中心間の指定されたパスが最短パスに準拠しているかどうかを確認するには、次のように信頼できる最短パスを使用して、指定されたパスに沿ったエッジ全体の重みを同じ中心の組み合わせ間の最短距離と比較することで計算できます。ダイクストラの計算またはフロイド・ウォーシャルの計算。特定のパス上のすべてのエッジの重みが最も制限された削除に一致する場合、それは最も単純なパスを表します。また、エッジの重み全体が最短距離よりも目立つ場合は、グラフ内の 2 つの中心間の距離が短いことを示します。使用される手法 ダイクストラのアルゴリズム 限界反転を伴うフロイド・ウォーシャル アルゴリズム コスト貪欲アルゴリズム ダイクストラの計算は、一般的なグラフ走査計算である可能性があります
 C プログラムで、次の内容を中国語に翻訳します。 リンクされたリストの下から n 番目のノードを検索するプログラム
Sep 13, 2023 pm 03:13 PM
C プログラムで、次の内容を中国語に翻訳します。 リンクされたリストの下から n 番目のノードを検索するプログラム
Sep 13, 2023 pm 03:13 PM
n 個のノードがある場合、タスクはリンク リストの最後に n 番目のノードを出力することです。プログラムはリスト内のノードの順序を変更してはなりませんが、リンクされたリストの最後のノードから n 番目のノードのみを出力する必要があります。例 Input-:102030405060 N=3Output-:40 上記の例では、最初のノードから開始して count-n 個のノード、つまり 10,2030,40,50,60 まで移動するため、最後から 3 番目のノードは 40 になります。 。リスト全体を効率的に走査する代わりに、次のアプローチを使用できます。たとえば、ノード タイプの temp への一時ポインタを取得し、この一時ポインタをヘッド ポインタが指す最初のノードに設定し、カウンタをリスト内のノードに設定します。
 ChatGPT プラグインを使用すると、ノードになりますが、センターではなくなります。
Apr 04, 2023 am 11:45 AM
ChatGPT プラグインを使用すると、ノードになりますが、センターではなくなります。
Apr 04, 2023 am 11:45 AM
OpenAI は、ロボットとロボットの対話の世界における結節点 (ただし重要な結節点) ではありますが、中心ではありません。 ChatGPT はプラグイン メカニズムを開始しました。これは非常にエキサイティングな開発です。全員が異口同音に「OSが誕生した」とコメントした。この発言は完全に間違っています。 OpenAI は、ロボットとロボットの対話の世界における結節点 (ただし重要な結節点) ではありますが、中心ではありません。私の心の中には、ロボットがロボットと会話する世界というイメージが常にありました。人々はロボットとチャットし、ロボットの友人を通じて人間がタスクを完了するのをロボットに手伝ってもらいます。 ChatGPT プラグインは世界を完璧に示します




