経度と緯度に基づいて地球上の 2 点間の距離を計算する JS 実装コード_JavaScript スキル
JS を使用して経度と緯度に基づいて地球上の 2 点間の距離を計算する
最近、経度と緯度に基づいて地球表面の 2 点間の距離を計算する式を使用し、JS を使用して実装しました。
地球の表面上の 2 点間の距離を計算するには、大まかに 2 つの方法があります。
最初の では、地球が滑らかな球面であると仮定し、任意の 2 点間の距離を計算します。この距離は大圏距離と呼ばれます。
式は次のとおりです:
JS を使用して次のように実装します:
var EARTH_RADIUS = 6378137.0; //Unit M
var PI = Math.PI;
function getRad(d){
return d*PI/ 180.0;
}
/**
* 大圏距離を計算します
* @param {Object} lat1
* @param {Object} lng1
* @param {Object} lat2
* @param {Object} lng2
*/
関数 getGreatCircleDistance(lat1,lng1,lat2,lng2){
var radLat1 = getRad(lat1); radLat2 = getRad(lat2);
var a = radLat1 - radLat2;
var b = getRad(lng1) - getRad(lng2); (Math.sqrt(Math.pow (Math.sin(a/2),2) Math.cos(radLat1)*Math.cos(radLat2)*Math.pow(Math.sin(b/2),2)) );
s = s *EARTH_RADIUS;
s = Math.round(s*10000)/10000.0;
を返します。式はほとんどの場合正しいですが、球上の相対点を扱う場合にのみ問題が発生します。
修正された式がありますが、必要がないため見つかりませんでした。Wiki で確認できます。 。
もちろん、地球は実際には球ではなく楕円体であることは誰もが知っているので、次の公式があります:
コードをコピー
コードは次のとおりです:
var f = getRad ( (lat1 lat2)/2);
var g = getRad((lat1 - lat2)/2);
var l = getRad((lng1 - lng2)/2); sg = Math.sin(g);
var sl = Math.sin(l);
var s,c,w,r, d ,h1,h2;
var a = EARTH_RADIUS;
sg = sl*sl; sf *sf;
s = sg*(1-sl) (1-sf)*sl;
c = (1-sg)*(1-sl)
w = Math.atan(Math.sqrt(s/c));
r = Math.sqrt(s*c)/w;
d = 2*w*a; = (3*r -1)/2/c;
h2 = (3*r 1)/2/s;
return d*(1 fl*(h1*sf*(1-) sg ) - h2*(1-sf)*sg));
}
もちろん、この式で計算された結果は、最終結果の経度よりも優れています。実際には、渡される座標の精度によって異なります。

ホットAIツール

Undresser.AI Undress
リアルなヌード写真を作成する AI 搭載アプリ

AI Clothes Remover
写真から衣服を削除するオンライン AI ツール。

Undress AI Tool
脱衣画像を無料で

Clothoff.io
AI衣類リムーバー

AI Hentai Generator
AIヘンタイを無料で生成します。

人気の記事

ホットツール

メモ帳++7.3.1
使いやすく無料のコードエディター

SublimeText3 中国語版
中国語版、とても使いやすい

ゼンドスタジオ 13.0.1
強力な PHP 統合開発環境

ドリームウィーバー CS6
ビジュアル Web 開発ツール

SublimeText3 Mac版
神レベルのコード編集ソフト(SublimeText3)

ホットトピック
 7488
7488
 15
15
 1377
1377
 52
52
 77
77
 11
11
 19
19
 40
40
 3D 空間内の 3 点間の距離を計算する C プログラム
Aug 29, 2023 pm 12:41 PM
3D 空間内の 3 点間の距離を計算する C プログラム
Aug 29, 2023 pm 12:41 PM
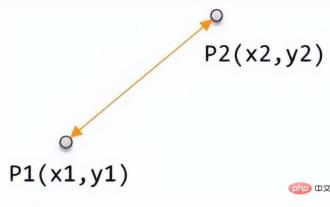
3 次元平面、つまり 3 つの座標が与えられた場合、タスクは指定された点間の距離を見つけて結果を表示することです。 3 次元平面上には 3 つの座標軸があり、x 軸の座標は (x1, y1, z1)、y 軸の座標は (x2, y2, z2) であり、 z 軸は (x3, y3, z) です。次のような、それらの間の距離を計算するための直接式があります。 $$\sqrt{\lgroupx2-x1\rgroup^{2}+\lgroupy2-y1\rgroup^{2}+\lgroupz2-z1\rgroup^{2 } }$$以下は 3 つの異なる座標軸とその座標を示す図です。以下の方法は次のとおりです。 -入力座標 (x1,
 機械学習に基づいた数値距離: 空間内の点間の距離
Apr 11, 2023 pm 11:40 PM
機械学習に基づいた数値距離: 空間内の点間の距離
Apr 11, 2023 pm 11:40 PM
この記事は WeChat 公開アカウント「情報時代に生きる」から転載したものであり、著者は情報時代に生きています。この記事を転載するには、情報時代の暮らしの公開アカウントまでご連絡ください。機械学習では、2 つのサンプル間の類似性とカテゴリ情報を評価するために、2 つのサンプル間の差異をどのように判断するかが基本的な概念です。この類似性を判断する尺度は、特徴空間内の 2 つのサンプル間の距離です。さまざまなデータ特性に基づいた多くの測定方法があります。一般的に言えば、2 つのデータ サンプル x、y に対して、関数 d(x, y) を定義します。これが 2 つのサンプル間の距離として定義される場合、d(x, y) は次の基本特性を満たす必要があります。負性: d(x, y)>=0 恒等式: d(x, y)=0 ⇔ x=y のペア
 iOS 17で画面距離を有効にして使用する方法
Jun 29, 2023 pm 01:37 PM
iOS 17で画面距離を有効にして使用する方法
Jun 29, 2023 pm 01:37 PM
Appleは年次開発者会議で、同社の一連のデバイスを強化する次世代オペレーティングシステムを発表した。いつものように、iOS 17 はすべての主要な変更点の中心であり、ライブ ボイスメール、メッセージの文字起こし、ライブ ステッカー、スタンバイ モード、全画面ライブ アクティビティ、インタラクティブ ウィジェットなどの機能を備えています。これらの新機能の中で際立っている機能の 1 つは、画面距離です。これは、iPhone 画面の目の疲れや近視の予防に重点を置いた健康中心の機能です。この記事では、画面距離とは何か、iOS17で画面距離を有効にする方法について説明します。 iOS17の画面距離とは何ですか? iOS 17 で導入された新しい健康機能の一部として、Apple はユーザーが健康状態を予測できるようにする画面距離機能を提供しています。
 iOS 17: iPhone で画面距離を有効にして使用する方法
Sep 21, 2023 pm 02:25 PM
iOS 17: iPhone で画面距離を有効にして使用する方法
Sep 21, 2023 pm 02:25 PM
iOS17アップデートの画面距離機能とは何ですか? Apple は、ユーザーが目の疲れや近視のリスクを防ぐために、iPhone に画面距離機能を提供しています。この機能 (iOS 17 以降で利用可能) は、iPhone の TrueDepth カメラ (FaceID にも役立つのと同じカメラ) を使用して、顔と電話の間の距離を測定します。画面の距離によって、iPhone を 12 インチまたは 30 センチメートル未満に長時間保持していることが検出されると、iPhone の画面から距離を保つように求めるメッセージが表示されます。デバイスが顔から 12 インチ未満にあることを検出すると、画面に「iPhone が近すぎます」というメッセージが表示され、視力を保護するために距離を保つ必要があるとアドバイスされます。デバイスを遠くに置いた場合のみ
 百度地図で経度と緯度を表示する方法 経度と緯度を表示する方法
Mar 12, 2024 pm 12:10 PM
百度地図で経度と緯度を表示する方法 経度と緯度を表示する方法
Mar 12, 2024 pm 12:10 PM
このプラットフォームを使用すると、すべての場所に座標があることがわかります。地理を学んだ学生なら、経度と緯度の座標が何であるかを知っていると思います。上記の機能は非常に強力であると言えます。あなたの場所をリアルタイムで知ることができますが、現在の経度と緯度を知ることもできます。つまり、誰もが地図上の任意の場所の経度と緯度の座標を確認することができます。このようにして、私たちは知ることができます。対応する特定の場所はより正確に表示されますが、知らないユーザーの大多数がまだそれを閲覧しているため、よりよく理解するために、今すぐエディターに参加しましょう。見てください。見逃さないと思います。それ、見に来てください。
 Googleマップで緯度と経度を確認する方法
Mar 24, 2024 pm 05:31 PM
Googleマップで緯度と経度を確認する方法
Mar 24, 2024 pm 05:31 PM
Google マップでは緯度と経度を確認できますが、緯度と経度はどのように確認すればよいでしょうか? ユーザーは場所の情報をクリックし、さらに表示をクリックすると、特定の経度と緯度の情報が表示されます。今回の経度と緯度の確認方法の紹介では具体的な内容が分かりますが、以下に詳細な方法を記載しておりますので、ぜひご覧ください。 Google マップで緯度と経度を確認する方法 A: 場所をクリックして選択すると、詳細情報が表示されます。詳細な紹介: モバイル版: 1. まず、進行状況マップに移動し、表示したい場所を選択します。 2. 中にある「すべて表示」ボタンをクリックします。 3. 詳細な緯度経度が確認できます。 PC 版: 1. まず、Google マップ Web サイトに入ります。 https://www.google.cn2. 右クリックして目的の場所を表示し、「ここにあるもの」をクリックします。
 UWB基地局の作動距離が伸び続ける理由 - IOTE Internet of Things Exhibition
Nov 27, 2023 pm 01:21 PM
UWB基地局の作動距離が伸び続ける理由 - IOTE Internet of Things Exhibition
Nov 27, 2023 pm 01:21 PM
産業アプリケーション市場における UWB 技術には興味深い傾向が現れています: 基地局の伝送距離は徐々に増加しています。典型的なシーンはトンネルや鉱山です。このシーンの特徴は、空間が直線的で、基地局の数が少ないことです。 UWB基地局も直線状に配置されています。基地局の作動距離が遠ければ遠いほど、プロジェクトに必要な基地局の数が減り、プロジェクトのコストが下がりますが、市場競争の下、市場の UWB 基地局の作動距離はますます遠くなります。基地局の作動距離は初期の数万メートルから、100メートル、200メートル、500メートル、1000メートル、2000メートル、あるいはそれ以上にまで拡大しました。この記事では、この背後にあるビジネス ロジックについてはあまり説明しません。なぜ UWB 基地局はますます遠く離れた場所でも動作するのでしょうか?重要なコンポーネントは 2 つあり、1 つはアンテナ、もう 1 つはアンテナです。
 Java コードを使用して、百度地図に現在地の緯度と経度を表示するにはどうすればよいですか?
Aug 06, 2023 pm 08:48 PM
Java コードを使用して、百度地図に現在地の緯度と経度を表示するにはどうすればよいですか?
Aug 06, 2023 pm 08:48 PM
Java コードを使用して、百度地図に現在地の緯度と経度を表示するにはどうすればよいですか? Baidu Maps は、地理位置情報関連のアプリケーションを開発するときによく使用される、非常に人気のある地図アプリケーションです。この記事では、Javaコードを使用して百度地図上に現在地の経度と緯度を表示する方法を紹介します。まず、Baidu 開発者アカウントを準備し、API キーを取得するためのアプリケーションを作成する必要があります。 Baidu 開発者 Web サイトにアカウントを登録してログインした後、コンソールでアプリケーションを作成し、アクセスするための API キーを取得できます。




