公理的トレーニングにより、LLM は因果推論を学習できます。6,700 万個のパラメータ モデルは、1 兆個のパラメータ レベル GPT-4 に匹敵します。

LLM に因果連鎖を見せると、LLM は公理を学習します。

AI はすでに数学者や科学者の研究を支援しています。たとえば、有名な数学者 Tao Zhexuan は、GPT やその他の AI ツールを活用した研究と探索の経験を繰り返し共有しています。 AI がこれらの分野で競争するには、強力で信頼性の高い因果推論機能が不可欠です。

この記事で紹介する研究では、小さなグラフの因果推移性公理の実証でトレーニングされた Transformer モデルが、大きなグラフの推移性公理に一般化できることがわかりました。

言い換えれば、Transformer が単純な因果推論の実行を学習すれば、より複雑な因果推論に使用できる可能性があります。チームが提案した公理トレーニングフレームワークは、受動的データに基づいて因果推論を学習するための新しいパラダイムであり、実証が十分である限り任意の公理を学習するために使用できます。

はじめに

因果推論は、因果関係に特化した事前定義された公理または規則に準拠する一連の推論プロセスとして定義できます。たとえば、d 分離 (有向分離) および do 計算ルールは公理と考えることができ、コライダー セットまたはバックドア セットの仕様は公理から導出されるルールと考えることができます。

一般的に言えば、因果推論ではシステム内の変数に対応するデータが使用されます。公理やルールは、正則化、モデル アーキテクチャ、または特定の変数の選択を通じて、帰納的バイアスの形で機械学習モデルに統合できます。

利用可能なデータタイプ (観察データ、介入データ、反事実データ) の違いに基づいて、Judea Pearl によって提案された「因果ラダー」は、因果推論の可能なタイプを定義します。

公理は因果関係の基礎であるため、機械学習モデルを直接使用して公理を学習できるかどうか疑問に思わずにはいられません。つまり、公理を学習する方法が、何らかのデータ生成プロセスを介して取得されたデータを学習することではなく、公理の記号的証明を直接学習すること (つまり、因果推論を学習すること) である場合はどうなるでしょうか?

特定のデータ分布を使用して構築されたタスク固有の因果モデルと比較して、このようなモデルには利点があります。それは、さまざまな異なる下流シナリオで因果推論を達成できることです。この問題は、言語モデルが自然言語で表現された記号データを学習する機能を獲得するにつれて重要になります。

実際、最近の研究では、自然言語で因果推論問題をエンコードするベンチマークを作成することで、大規模言語モデル (LLM) が因果推論を実行できるかどうかを評価しています。

マイクロソフト、マサチューセッツ工科大学、インド工科大学ハイデラバード校 (IIT ハイデラバード) の研究チームも、この方向で重要な一歩を踏み出しました。それは、公理的トレーニング を通じて因果推論を学習するための 方法を提案するというものです。

• 論文のタイトル: 公理的トレーニングによるトランスフォーマーの因果推論の教育
• 論文のアドレス: https://arxiv.org/pdf/2407.07612

公理的トレーニング

彼らは次のように想定しています。因果公理は、次のような記号タプル〈前提、仮説、結果〉として表現できます。このうち、仮説は仮説、つまり因果関係のステートメントを指し、前提はステートメントが「真実」であるかどうかを判断するために使用される関連情報を指し、結果は当然のことです。結果は単純な「はい」または「いいえ」になります。

たとえば、「大規模言語モデルは相関関係から因果関係を推測できるか?」という論文のコライダー公理は次のように表現できます: 、結論は「はい」です。

このテンプレートに基づいて、変数名、変数番号、変数の順序などを変更することで、多数の合成タプルを生成できます。

Transformer を使用して因果公理を学習し、公理トレーニングを達成するために、チームは次の方法を使用してデータセット、損失関数、位置埋め込みを構築しました。

公理トレーニング: データセット、損失関数、位置のコンパイル

トレーニングデータ

特定の公理に基づいて、「仮説」を「前提」に基づいて適切なラベルにマッピングできます（ はい、もしくは、いいえ）。トレーニング データ セットを作成するために、チームは特定の変数設定 X、Y、Z、A の下で考えられるすべてのタプル {(P, H, L)}_N を列挙します。ここで、P は前提、H は仮説、L はラベルです（はい、もしくは、いいえ）。

何らかの因果関係図に基づく前提 P が与えられた場合、仮説 P が特定の公理 (1 回以上) を使用して導出できる場合、ラベル L は Yes であり、それ以外の場合は No です。

たとえば、システムの基礎となる実際の因果グラフに、X_1 → X_2 → X_3 →・・・→ X_n というチェーン トポロジーがあるとします。次に、考えられる前提は X_1 → X_2 ∧ X_2 → X_3 であり、X_1 →上記の公理は帰納的に何度も使用して、より複雑なトレーニング タプルを生成できます。

トレーニング設定では、推移性公理によって生成された N 個の公理インスタンスを使用して合成データセット D を構築します。 D の各インスタンスは (P_i, H_ij, L_ij) の形式で構成されます。ここで、n は各 i 番目の前提内のノードの数です。 P は前提、つまり、特定の因果構造の自然言語表現 (X が Y を引き起こす、Y が Z を引き起こすなど) であり、その後に質問 H (X は Y を引き起こすかなど) が続きます。またはいいえ)。この形式は、特定の因果関係グラフ内の各固有のチェーンのノードのすべてのペアを効果的にカバーします。

損失関数

データセットが与えられると、損失関数は各タプルのグラウンドトゥルースラベルに基づいて定義され、次のように表現されます: 分析は、この損失を使用して、次のトークン予測と比較したことを示します。有望な結果が得られる可能性があります。

位置エンコーディング

トレーニング関数と損失関数に加えて、位置エンコーディングの選択ももう 1 つの重要な要素です。位置エンコーディングは、シーケンス内のトークンの絶対位置および相対位置に関する重要な情報を提供できます。

有名な論文「attention is all you need」では、周期関数 (サイン関数またはコサイン関数) を使用してこれらのコードを初期化する絶対位置コーディング戦略を提案しています。

絶対位置エンコーディングは、任意のシーケンス長のすべての位置に特定の値を提供できます。しかし、いくつかの研究では、絶対位置エンコーディングは Transformer の長さ一般化タスクに対処するのが難しいことが示されています。学習可能な APE バリアントでは、各位置の埋め込みがランダムに初期化され、モデルを使用してトレーニングされます。この方法は、新しい位置の埋め込みがまだトレーニングされておらず、初期化されていないため、トレーニング中のシーケンスよりも長いシーケンスに対処するのに苦労します。

興味深いことに、最近の発見により、自己回帰モデルの位置埋め込みを削除するとモデルの長さ汎化能力が向上し、自己回帰デコード中のアテンション メカニズムは位置情報をエンコードするのに十分であることが示されました。チームは、学習可能な位置エンコーディング (LPE)、正弦波位置エンコーディング (SPE)、位置エンコーディングなし (NoPE) など、因果関係のあるタスクにおける汎化への影響を理解するために、さまざまな位置エンコーディングを使用しました。

モデルの一般化能力を向上させるために、チームは長さ、ノード名、チェーンの順序、分岐ステータスの摂動を含むデータ摂動も使用しました。

実験

次の疑問が生じます: モデルがこのデータを使用してトレーニングされた場合、モデルはこの公理を新しいシナリオに適用することを学習できますか?

この質問に答えるために、チームは因果的に独立した公理のこの象徴的なデモンストレーションを使用して、Transformer モデルをゼロからトレーニングしました。

汎化パフォーマンスを評価するために、サイズ 3 ～ 6 ノードの単純な因果的に独立した公理チェーンでトレーニングし、長さ汎化パフォーマンス (サイズ 7 ～ 15 のチェーン)、名前など、汎化パフォーマンスのいくつかの異なる側面をテストしました。一般化 (長い変数名)、逐次一般化 (エッジが反転したチェーンまたはノードがシャッフルされたチェーン)、構造的一般化 (分岐のあるグラフ)。図 1 は、Transformer の構造的一般化を評価する方法を示しています。

具体的には、GPT-2 アーキテクチャに基づいた 6,700 万個のパラメーターを備えたデコーダーベースのモデルをトレーニングしました。モデルには 12 のアテンション レイヤー、8 つのアテンション ヘッド、および 512 の埋め込み次元があります。彼らは、各トレーニング データセットでモデルをゼロからトレーニングしました。位置エンベディングの影響を理解するために、彼らは 3 つの位置エンベディング設定、正弦波位置エンコーディング (SPE)、学習可能な位置エンコーディング (LPE)、および位置エンコーディングなし (NoPE) についても調査しました。

結果を表 1、図 3、図 4 に示します。

表 1 は、トレーニング中には見ら​​れないより大きな因果連鎖で評価した場合のさまざまなモデルの精度を示しています。新しいモデル TS2 (NoPE) のパフォーマンスは、兆パラメータ スケールの GPT-4 に匹敵することがわかります。

図 3 は、長いノード名 (トレーニング セットよりも長い) を持つ因果シーケンスと、異なる位置の埋め込みの影響に対する汎化能力評価の結果です。

図 4 は、より長い目に見えない因果シーケンスに対する汎化能力を評価します。

彼らは、単純なチェーンでトレーニングされたモデルは、より大きなチェーン上の公理の複数の適用に一般化できるが、逐次的または構造的一般化などのより複雑なシナリオには一般化できないことを発見しました。ただし、モデルが単純なチェーンとランダムな逆エッジを持つチェーンで構成される混合データセットでトレーニングされた場合、モデルはさまざまな評価シナリオによく一般化します。

NLP タスクの長さの一般化に関する結果を拡張して、長さとその他の次元にわたる因果的一般化を確実にする上で位置埋め込みの重要性を発見しました。彼らの最高のパフォーマンスのモデルには位置エンコーディングがありませんでしたが、場合によっては正弦波エンコーディングがうまく機能することもわかりました。

この公理トレーニング方法は、図 5 に示すように、より難しい問題に一般化することもできます。つまり、統計的独立性の記述を含む前提に基づいて、タスクの目標は相関関係と因果関係を識別することです。このタスクを解決するには、d 分離やマルコフ特性など、いくつかの公理の知識が必要です。

チームは、上記と同じ方法を使用して合成トレーニング データを生成し、その後、3 ～ 4 つの変数を含むタスクのデモンストレーションでトレーニングされた Transformer が、5 つの変数を含む問題を解決することを学習できることがわかりました。タスク。そして、このタスクでは、モデルは GPT-4 や Gemini Pro などのより大きな LLM よりも正確です。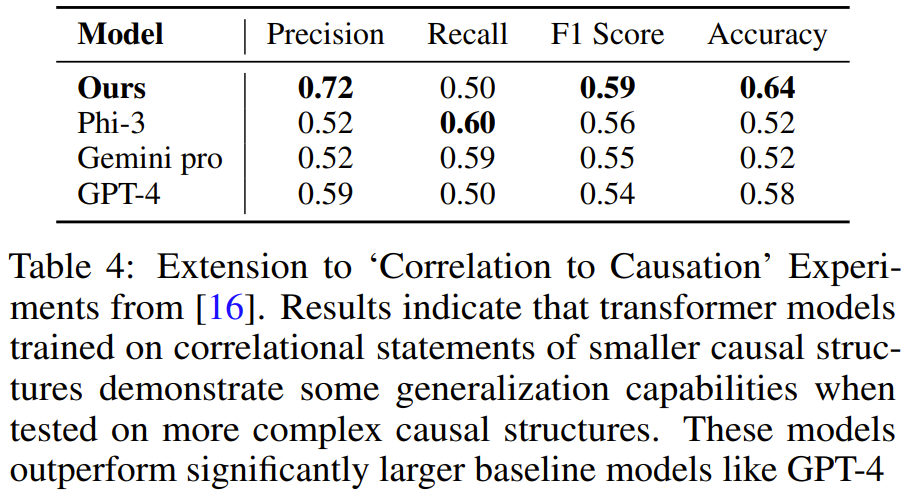

チームは次のように述べています。「私たちの研究は、公理の象徴的な実証を通じて因果推論を学習するための新しいパラダイムをモデルに提供します。これを公理トレーニングと呼びます。この方法のデータ生成とトレーニングは一般的です。」公理はシンボリックタプルの形式で表現できるため、この方法を使用して学習できます。

以上が公理的トレーニングにより、LLM は因果推論を学習できます。6,700 万個のパラメータ モデルは、1 兆個のパラメータ レベル GPT-4 に匹敵します。の詳細内容です。詳細については、PHP 中国語 Web サイトの他の関連記事を参照してください。