バックトラッキングを使用した 8 つのクイーン問題の解決

8 人のクイーンの問題は、2 人のクイーンが互いに攻撃できないように、チェス盤の各列にクイーンを配置する解決策を見つけることです。この問題は再帰を使用して解決できます。このセクションでは、この問題を解決するためのバックトラッキングと呼ばれる一般的なアルゴリズム設計手法を紹介します。バックトラッキングアプローチでは、候補となる解決策を段階的に検索し、
が問題であると判断するとすぐにそのオプションを放棄します。 候補は有効な解決策である可能性が低いため、新しい候補を探します。

2 次元配列を使用してチェス盤を表すことができます。ただし、各行に含めることができるクイーンは 1 つだけであるため、行内のクイーンの位置を示すには 1 次元配列を使用するだけで十分です。したがって、queens 配列を次のように定義できます。

int[] クイーン = new int[8];

j を queens[i] に代入して、クイーンが行 i と列 j に配置されることを示します。下の図 (a) は、下の図 (b) のチェス盤の queens 配列の内容を示しています。

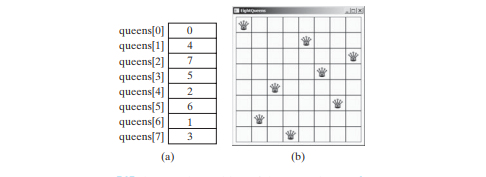
検索は、k = 0 の最初の行から開始されます。k は、考慮されている現在の行のインデックスです。このアルゴリズムは、_j = 0, 1, ... , 7 の行の j_ 番目の列にクイーンを配置できる可能性があるかどうかをこの順序でチェックします。検索は次のように実装されます:

• 成功した場合は、次の行のクイーンの配置を探し続けます。現在の行が最後の行であれば、解決策が見つかります。
• 成功しない場合は、前の行に戻り、前の行の次の列で新しい配置の検索を続けます。
• アルゴリズムが最初の行に戻り、この行でクイーンの新しい配置を見つけることができない場合、解決策は見つかりません。

以下のコードは、Eight Queens 問題の解決策を表示するプログラムを示します。

package application;
import javafx.application.Application;
import javafx.geometry.Pos;
import javafx.stage.Stage;
import javafx.scene.Scene;
import javafx.scene.control.Label;
import javafx.scene.image.Image;
import javafx.scene.image.ImageView;
import javafx.scene.layout.GridPane;

public class EightQueens extends Application {
    public static final int SIZE = 8; // The size of the chess board
    // queens are placed at (i, queens[i])
    // -1 indicates that no queen is currently placed in the ith row
    // Initially, place a queen at (0, 0) in the 0th row
    private int[] queens = {-1, -1, -1, -1, -1, -1, -1, -1};

    @Override // Override the start method in the Application class
    public void start(Stage primaryStage) {
        search(); // Search for a solution

        // Display chess board
        GridPane chessBoard = new GridPane();
        chessBoard.setAlignment(Pos.CENTER);
        Label[][] labels = new Label[SIZE][SIZE];
        for(int i = 0; i < SIZE; i++)
            for(int j = 0; j < SIZE; j++) {
                chessBoard.add(labels[i][j] = new Label(), i, j);
                labels[i][j].setStyle("-fx-border-color: black");
                labels[i][j].setPrefSize(55, 55);
            }

        // Display queens
        Image image = new Image("file:C:/Users/Paul/development/MyJavaFX/src/application/image/lo.jpg");
        for(int i = 0; i < SIZE; i++)
            labels[i][queens[i]].setGraphic(new ImageView(image));

        // Create a scene and place it in the stage
        Scene scene = new Scene(chessBoard, 55 * SIZE, 55 * SIZE);
        primaryStage.setTitle("EightQueens"); // Set the stage title
        primaryStage.setScene(scene); // Place the scene in the stage
        primaryStage.show(); // Display the stage
    }

    public static void main(String[] args) {
        Application.launch(args);
    }

    /** Search for a solution */
    private boolean search() {
        // k - 1 indicates the number of queens placed so far
        // We are looking for a position in the kth row to place a queen
        int k = 0;
        while(k >= 0 && k < SIZE) {
            // Find a position to place a queen in the kth row
            int j = findPosition(k);
            if(j < 0) {
                queens[k] = -1;
                k--; // back track to the previous row
            } else {
                queens[k] = j;
                k++;
            }
        }

        if(k == -1)
            return false; // No solution
        else
            return true; // A solution is found
    }

    public int findPosition(int k) {
        int start = queens[k] + 1; // Search for a new placement

        for(int j =start; j < SIZE; j++) {
            if(isValid(k, j))
                return j; // (k, j) is the place to put the queen now
        }

        return -1;
    }

    /** Return true is a queen can be placed at (row, column) */
    public boolean isValid(int row, int column) {
        for(int i = 1; i <= row; i++)
            if(queens[row - i] == column // Check column
            || queens[row - i] == column - i // Check upleft diagonal
            || queens[row - i] == column + i) // Check upright diagonal
                return false; // There is a conflict
        return true; // No conflict
    }

}

プログラムは、解決策を検索するために search() (行 20) を呼び出します。最初は、どの行にもクイーンは配置されていません (16 行目)。検索は k = 0 の最初の行から開始され (53 行目)、女王の場所を見つけます (56 行目)。成功した場合は、その行 (行 61) に配置し、次の行 (行 62) を検討します。成功しなかった場合は、前の行 (58 ～ 59 行目) に戻ります。

findPosition(k) メソッドは、queen[k] + 1 から始まる行 k にクイーンを配置できる位置を検索します (行 73) ）。 start、start + 1、 にクイーンを配置できるかどうかをチェックします。 。 。 、7 の順です (75 ～ 78 行目)。可能であれば、列インデックスを返します (77 行目)。それ以外の場合は、-1 を返します (80 行目)。

isValid(row, column) メソッドが呼び出され、指定された位置にクイーンを配置することで、以前に配置されたクイーンと競合するかどうかがチェックされます (76 行目)。以下の図に示すように、同じ列 (86 行目)、左上の対角線 (87 行目)、または右上の対角線 (88 行目) にクイーンが配置されないようにします。

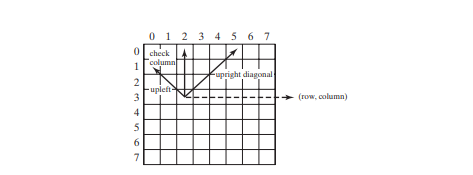
以上がバックトラッキングを使用した 8 つのクイーン問題の解決の詳細内容です。詳細については、PHP 中国語 Web サイトの他の関連記事を参照してください。