オッズを打ち破る: カジノ利益の背後にある数学

なぜカジノがいつも勝っているように見えるのか疑問に思ったことはありますか? 「オッズを打ち破る: カジノ利益の背後にある数学」では、カジノが長期的に利益を確実に得るための単純な数学と巧妙な戦略を探ります。わかりやすい例とモンテカルロシミュレーションを通じて、ハウスエッジの背後にある秘密を明らかにします。カジノがどのようにオッズを有利に変えるのかを知る準備をしてください!

ハウスエッジを理解する

ハウスエッジはカジノの世界における基本的な概念です。これは、プレイヤーが賭けた各賭けからカジノが期待する平均利益を表します。本質的に、カジノが長期的に保持する各賭け金の割合です。

ハウスエッジが存在するのは、カジノがゲームの「真のオッズ」に従って勝ちの賭け金を支払わないためです。真のオッズは、イベントが発生する実際の確率を表します。カジノは、わずかに低いオッズで支払いを行うことで、長期的に確実に利益を上げます。

ハウスエッジ (HE) は、プレーヤーの元の賭け金のパーセンテージとして表されるカジノ利益として定義されます。

** ヨーロピアン ルーレット ** には緑のゼロが 1 つだけあり、合計 37 の数字になります。プレーヤーが赤に 1 ドルを賭けた場合、1 ドルを獲得する確率は 18/37 で、1 ドルを失う確率は 19/37 です。期待値は次のとおりです:

期待値=( 1 × 18/37 )+( −1 × 19/37 )= 18/37 − 19/37 = −1/37 ≈ −2.7%

したがって、ヨーロピアン ルーレットのハウス エッジ (HE) は 2.7% 程度です。

もっと理解するために、自分だけのゲーム、シンプルなサイコロロールゲームを作ってみましょう。

import random

def roll_dice():
    roll = random.randint(1, 100)

    if roll == 100:
        print(roll, 'You rolled a 100 and lost. Better luck next time!')
        return False
    elif roll <= 50:
        print(roll, 'You rolled between 1 and 50 and lost.')
        return False
    else:
        print(roll, 'You rolled between 51 and 99 and won! Keep playing!')
        return True

このゲームでは:

• 出目が 100 の場合、プレイヤーは 1/100 の確率で負けます。

• 出目が 1 ～ 50 の場合、プレイヤーは 50/100 の確率で負けます。

• 出目が 51 から 99 の間の場合、プレイヤーが勝つ確率は 49/100 です。

期待値 =(1× 49/100 ) + ( −1× 51/100 ) = 49/100 − 51/100 ＝ −2/100 ≈ −2%

したがって、ハウスエッジは2%です。

モンテカルロ シミュレーションを理解する

モンテカルロ シミュレーションは、プロセスの多数のシミュレーションを実行し、結果を観察することにより、複雑なシステムを理解して予測するために使用される強力なツールです。カジノのコンテキストでは、モンテカルロ シミュレーションはさまざまな賭けのシナリオをモデル化し、ハウス エッジがどのように長期的な収益性を確保するかを示すことができます。モンテカルロ シミュレーションがどのように機能するのか、そしてそれを簡単なカジノ ゲームにどのように適用できるのかを見てみましょう。

モンテカルロ シミュレーションとは何ですか?

モンテカルロ シミュレーションでは、確率変数を生成してプロセスを複数回シミュレートし、結果を分析します。数千回、さらには数百万回の反復を実行することで、起こり得る結果の分布を取得し、さまざまなイベントの可能性についての洞察を得ることができます。

モンテカルロ シミュレーションをサイコロ ゲームに適用する

モンテカルロ シミュレーションを使用して、前に説明したサイコロロール ゲームをモデル化します。これは、ハウスエッジが時間の経過とともにゲームの収益性にどのような影響を与えるかを理解するのに役立ちます。

`def monte_carlo_simulation(trials):
    wins = 0
    losses = 0

    for _ in range(trials):
        if roll_dice():
            wins += 1
        else:
            losses += 1

    win_percentage = (wins / trials) * 100
    loss_percentage = (losses / trials) * 100
    houseEdge= loss_percentage-win_percentage
    print(f"After {trials} trials:")
    print(f"Win percentage: {win_percentage:.2f}%")
    print(f"Loss percentage: {loss_percentage:.2f}%")
    print(f"House Edge: {houseEdge:.2f}%")

# Run the simulation with 10,000,000 trials
monte_carlo_simulation(10000000)`

結果の解釈

このシミュレーションでは、サイコロロール ゲームを 10,000,000 回実行して、勝率と負け率を観察します。先ほど計算したハウスエッジ (2%) を考慮すると、損失率は勝率よりわずかに高くなることが予想されます。

シミュレーションを実行すると、次のような結果が表示される場合があります。

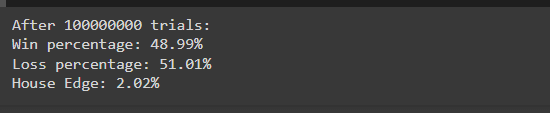
これらの結果は理論上の確率 (勝ち 49%、負け 51%) とほぼ一致しており、多数の試行にわたってハウスエッジがどのように現れるかを示しています。わずかな不均衡により、長期的にはカジノの収益性が確保されます。

短期的な利益と長期的な損失を視覚化する

モンテカルロ シミュレーションは、ランダムなサンプリングを繰り返すことで結果をモデリングおよび予測するのに強力です。ギャンブルの文脈では、モンテカルロ シミュレーションを使用して、さまざまな賭け戦略の潜在的な結果を理解できます。

各ラウンドで同じ最初の賭けをする 1 人のベッターをシミュレートし、指定された賭け数にわたってそのアカウントの価値がどのように変化するかを観察します。

Matplotlib を使用してベッティング ジャーニーをシミュレーションおよび視覚化する方法は次のとおりです。

def bettor_simulation(funds, initial_wager, wager_count):
    value = funds
    wager = initial_wager

    # Lists to store wager count and account value
    wX = []
    vY = []

    current_wager = 1

    while current_wager <= wager_count:
        if roll_dice():
            value += wager
        else:
            value -= wager

        wX.append(current_wager)
        vY.append(value)
        current_wager += 1

    return wX, vY

# Parameters for simulation
funds = 10000
initial_wager = 100
wager_count = 1000

# Run the simulation for a single bettor
wager_counts, account_values = bettor_simulation(funds, initial_wager, wager_count)

# Plotting the results
plt.figure(figsize=(12, 6))
plt.plot(wager_counts, account_values, label='Bettor 1', color='blue')
plt.xlabel('Wager Count')
plt.ylabel('Account Value')
plt.title('Betting Journey: Short-Term Wins vs Long-Term Losses')
plt.grid(True)
plt.legend()

# Highlighting the short-term and long-term trend
plt.axhline(y=funds, color='gray', linestyle='--', label='Initial Funds')
plt.axhline(y=account_values[0], color='green', linestyle='--', label='Starting Account Value')
plt.axhline(y=account_values[-1], color='red', linestyle='--', label='Final Account Value')

plt.legend()
plt.show()

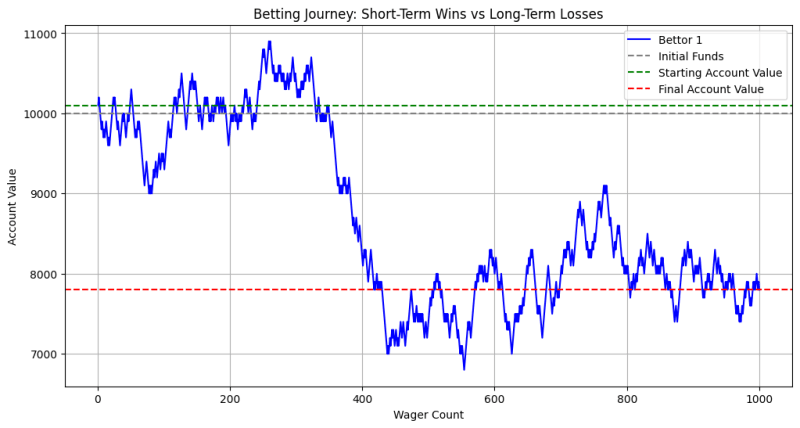
このグラフは、ベッターのアカウント価値が勝ち負けによって時間の経過とともにどのように変動するかを示しています。最初は勝ちの期間 (開始値の上の緑の線) が存在する可能性がありますが、賭けの数が増加するにつれて、ハウス エッジの累積効果が明らかになります。最終的には、ベッターの口座価値は初期資金 (灰色の線) に向かうかそれ以下に減少する傾向があり、長期的な損失を示します。

結論

カジノの利益の背後にある数学を理解すると、ハウスエッジの概念を通じて、すべてのゲームでハウスに明らかな利点があることがわかります。時々勝つこともありますが、カジノ ゲームに組み込まれた確率により、ほとんどのプレーヤーは時間の経過とともに確実にお金を失います。モンテカルロ シミュレーションはこれらのダイナミクスを鮮明に示しており、カジノの統計的優位性により、短期的な勝利であっても長期的な損失がどのように隠蔽されるかを示しています。カジノの収益性の数学的確実性に関するこの洞察は、情報に基づいた意思決定と責任あるギャンブルの実践の重要性を強調しています。

次に、さまざまなベッティング戦略を比較したり、さまざまな初期賭け金がベッターの結果に及ぼす影響を分析したりするなど、追加の視覚化やバリエーションを検討できます。

接続を維持:

• GitHub: ezhillragesh

• Twitter: ezhillragesh

• ウェブサイト:ragesh.me

遠慮せずに意見を共有し、質問し、ディスカッションに参加してください。

コーディングを楽しんでください!

以上がオッズを打ち破る: カジノ利益の背後にある数学の詳細内容です。詳細については、PHP 中国語 Web サイトの他の関連記事を参照してください。