
元のタイトル:「これら 3 つの Excel 財務関数は再び過小評価されています!」 》
この記事の著者:Xiaohua
この記事の編集者:Yanlan
最近、Xiaohuaは古い友人の魂から来た興味深い質問に遭遇しました:
毎月の年金と個人の支払い方法相互保険財政は選択をしますか?
これら 2 つの金融商品の基本情報は次のとおりです:
毎月の年金:
毎月 1,000 元を支払い、年利 3%、2 年間の期間、元金と利息を支払うことができます。満期時に一括で引き落とされます。
相互保険金融:
毎月1,000元の元金を支払い、毎月の元金は10%の利子で計算され、期間は2年間です。同じ商品に参加する人は 24 人で、毎月 1 人が他の人が支払った元金と利息をすべて受け取る必要があり、1 人は支払いを受け取った翌月に 100 元の利息を支払わなければなりません。
これら 2 つの金融商品の長所と短所を比較するにはどうすればよいですか?
この問題は、ターミナルバリュー法、収益率法、IRR法から考えることができ、ついでに金融関数の使用法もいくつか共有します。
ターミナルバリュー分析方法は、基準年、換算金利、キャッシュフローを決定した後、計画(プロジェクト)の純利益の最終価値を計算します。最終価値が高いほど、ソリューションの経済的実現可能性が高くなります。
等額年金の満期後に受け取れる元金と利息はいくらですか?この問題は、最終値関数FVを使用して計算できます。

年金将来価値計算式:
=-FV(B3/12,C3,A3)

毎月1,000元の年金が支払われる場合、金利は 3% で計算され、2 年後には元金と利息の合計 24,703 元が受け取れます。
「相互保険ファイナンス」の最終価値(ローリング投資がないと仮定した場合)は、元本と利息の引き落とし順序に関係し、引き落としが遅くなるほど収入が大きくなります。最終値は次のように計算されます:
=S2*U2+S2*T2*(V2-1)-S2*T2*(U2-V2)

最終値法の観点からは、確実に受け取りができれば、支払期間が16期以降の場合は「共済財政」の収入が月額年金より多くなります。 受取期間が16期より前の場合は「共済財政」の収入が少なくなります。毎月の年金よりも。
ターミナルバリュー法は、投資規模が同等の投資計画に適しています。
この暫定的な結論を古い友人に話したところ、彼は信じられない様子でこう尋ねました:
「相互保険金融」の名目金利はなぜ 10% しかないのですか?加入者の収入の/3は、還元率わずか3%の年金月額よりも高いのでしょうか?
これには収益性の計算が含まれます。
収益率法とは、投資プロジェクトの平均年間正味収益率と投資の資本コストを比較して、その投資が望ましいかどうかを判断し、以下の条件で投資計画を選択する投資意思決定方法です。利用可能な投資プランの中で最高の収益率。
明らかに、毎月の年金利回りは名目金利、つまり 3% と一致しています。
それでは、「共済金融」の支払期間ごとの還元率はどのくらいなのでしょうか?
RATE関数を使用して計算できます。

「相互保険金融」の収益率は以下のように計算されます。
=RATE(U2-S2,0,W2,0)*12

「相互保険ファイナンス」の名目金利は10%と高くなっていますが、実際には16期間後に元金と利息を受け取る場合に限り、それまでに受け取れば3%に達することもあります。利回りは毎月の年金収入よりも低くなります。 「共済金融」の利回りが依然として高いことがわかります。
しかし、「共済金融」の収益が毎月の年金に比べて劣っていると評価するのは不当である。その理由は、「共済」は、毎月の年金は満期まで元利金が回収できないからである。この部分があれば資金は再び投資に回され、「共済財政」は大きく改善されることになる。
財務管理では、この違いを説明するために時間価値がよく使用され、内部収益率 (IRR) と正味現在価値 (NPV) を使用して、投資の動的な収益を測定できます。
以下では、これら 2 つの金融商品を比較するために NPV を選択します。IRR 比較方法はこのケースには適用されません。

正味現在価値を計算する前に、各期間の 2 つの製品のキャッシュ フローをリストし、NPV 関数を使用して計算する必要があります。

Monatliche Zahlung von 1.000 Yuan für eine monatliche Rente. Nach 24 Zahlungen werden Kapital und Zinsen in Höhe von 24.703 Yuan in einer Summe zurückgezahlt. Der Cashflow und der Kapitalwert werden wie folgt berechnet:
=NPV(B3 /12,B2:Y2)

Hier wird der Zinssatz der monatlichen Rente direkt als Abzinsungssatz ausgewählt und sein Nettobarwert sollte 0 sein. Bei der Berechnung des Nettobarwerts von „Mutual Insurance Finance“ verwenden wir weiterhin diesen Abzinsungssatz. Wenn der Nettobarwert des letzteren größer als 0 ist, bedeutet dies, dass der Kapitalertrag des letzteren besser ist, andernfalls ist er schlechter.
„Mutual Insurance Finance“ hat mehrere mögliche Auszahlungsfristen, daher müssen wir bei der Berechnung des IRR dieses Produkts eine Simulationstabelle verwenden, um dies zu erreichen.
Kapitalwertberechnung „Mutual Insurance Finance“:
❶ Unter Berücksichtigung der Auszahlungsdauer als Variable wird der Cashflow jeder Periode, der auf der Grundlage der Variablen berechnet wird, aufgelistet.
Der Cashflow des Kapitals, eine positive Zahl bedeutet Zahlung und eine negative Zahl bedeutet Auszahlung.
=IF(E$4=$G$2,-$D$2*23,$D$2)
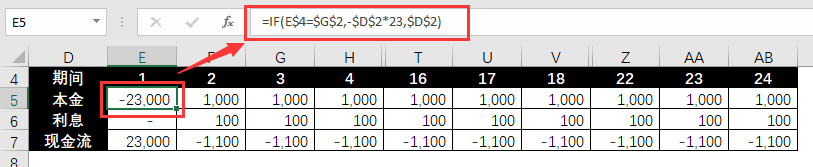
Der Cashflow der Zinsen, eine positive Zahl zeigt die Zahlung an und eine negative Zahl zeigt den Eingang an.
=IFS(E4$G$2,$D$2*$E$2)

Konsolidierter Cashflow:

❷ Berechnen Sie den IRR unter einem einzigen Auszahlungszeitraum.
=NPV(H2/12,E7:AB7)
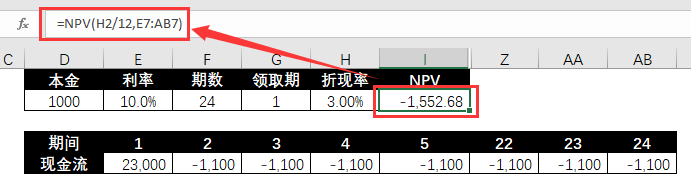
❸ Verwenden Sie die Simulationstabelle, um den NPV für verschiedene Extraktionszeiträume zu berechnen.
① Listen Sie die erforderlichen Variablenwerte für den Erfassungszeitraum auf und verknüpfen Sie die entsprechenden Ergebniswerte in der ersten Zeile.

② Wählen Sie die Linkzeile, den Variablenwertbereich und den Ergebniswertbereich aus und führen Sie die folgenden Schritte aus, um den Simulationsvorgang abzuschließen.

Die Ergebnisse der Simulationsberechnung lauten wie folgt:

Aus NPV-Sicht sind die Einnahmen aus „gegenseitiger Versicherungsfinanzierung“ und monatlicher Rente vergleichbar.
Bei allen Teilnehmern sind die Vergleichsrenditen gemischt. Dies liegt daran, dass Teilnehmer mit einem früheren Anspruchszeitraum schneller einen Mittelzufluss für rollierende Investitionen erzielen können, was in gewissem Maße eine Absicherung gegen den Verlust hoher Zinssätze darstellt.
Zusammenfassend lässt sich sagen: Wenn es unmöglich ist, eine fortlaufende Investition zu realisieren oder Sicherheit zu erreichen, sollten Sie sich für eine monatliche Rente als Investition entscheiden. Dieses Produkt bietet stabile Kapitalerträge und ein höheres durchschnittliches statisches Einkommen. Wenn Sie
höhere dynamische Renditen anstreben oder nach Abzug von Kapital und Zinsen Zweitinvestitionen tätigen möchten, sollten Sie sich für die Finanzverwaltung „Mutual Insurance Finance“ entscheiden. Letzteres bietet die Möglichkeit, einen höheren Nettobarwert und statische Renditen zu erzielen. Das Obige ist eine Erweiterung von Xiaohua aus einem Finanzproduktauswahlproblem. Es erklärt die Verwendung mehrerer Excel-Finanzformeln und -Funktionen, darunter:
❶ FV-Funktion und RATE-Funktion
❷ NPV-Funktion
❸ Simulationstabelle
Wenn Sie Finanzbuchhalter sind oder Bedarf oder Interesse an Finanzberechnungen haben, werden Ihnen diese Formeln und praktischen Fälle hilfreich sein.

以上が3 つの Excel 財務関数で複雑な財務計算を解決の詳細内容です。詳細については、PHP 中国語 Web サイトの他の関連記事を参照してください。