中国科学技術大学とファーウェイ・ノアは、大規模モデルのパフォーマンス、データ圧縮率、トレーニング損失の関係を明らかにするためにエントロピー法則を提案しました。

AIxiv专栏是本站发布学术、技术内容的栏目。过去数年，本站AIxiv专栏接收报道了2000多篇内容，覆盖全球各大高校与企业的顶级实验室，有效促进了学术交流与传播。如果您有优秀的工作想要分享，欢迎投稿或者联系报道。投稿邮箱：liyazhou@jiqizhixin.com；zhaoyunfeng@jiqizhixin.com

本工作由中科大认知智能全国重点实验室 IEEE Fellow 陈恩红团队与华为诺亚方舟实验室完成。陈恩红教授团队深耕数据挖掘、机器学习领域，在顶级期刊与会议上发表多篇论文，谷歌学术论文引用超两万次。诺亚方舟实验室是华为公司从事人工智能基础研究的实验室，秉持理论研究与应用创新并重的理念，致力于推动人工智能领域的技术创新和发展。

数据是大语言模型（LLMs）成功的基石，但并非所有数据都有益于模型学习。直觉上，高质量的样本在教授 LLM 上预期会有更好的效率。因此，现有方法通常专注于基于质量的数据选择。然而，这些方法中的大多数独立地评估不同的数据样本，忽略了样本之间复杂的组合效应。如图 1 所示，即使每个样本质量完美，由于它们的互信息冗余或不一致性，它们的组合可能仍然次优。尽管基于质量的子集由所有三个优质样本组成，但它们编码的知识实际上是冗余和冲突的。相比之下，另一个由几个相对较低质量但多样化的样本组成的数据子集在教授 LLM 方面可能传达更多信息。因此，基于质量的数据选择并未完全符合最大化 LLM 知识掌握的目标。

而本文旨在揭示 LLM 性能与数据选择之间的内在关系。受 LLM 信息压缩本质的启发，我们发现了一条 entropy law，它将 LLM 性能与数据压缩率和前几步模型训练的损失加以联系，分别反映了数据集的信息冗余程度和 LLM 对数据集中固有知识的掌握程度。通过理论推导和实证评估，我们发现模型性能与训练数据的压缩率呈负相关，而这通常会产生较低的训练损失。基于 entropy law 的发现，我们提出了一种非常高效且通用的数据选择方法用于训练 LLM，名为 ZIP，其旨在优先选择低压缩率的数据子集。ZIP 分多阶段、贪心地选择多样化的数据，最终获得一个具有良好多样性的数据子集。

• 团队：中科大认知智能全国重点实验室陈恩红团队，华为诺亚方舟实验室
• 论文链接: https://arxiv.org/pdf/2407.06645
• 代码链接: https://github.com/USTC-StarTeam/ZIP

O 図 1 tENTropy の法則

データ圧縮と LLM パフォーマンスの関係を理論的に分析します。直観的には、トレーニング データの正確さと多様性が最終モデルのパフォーマンスに影響します。同時に、データに重大な固有の矛盾がある場合、またはモデルがデータにエンコードされた情報を十分に把握していない場合、LLM のパフォーマンスは最適ではない可能性があります。これらの仮定に基づいて、LLM のパフォーマンスを Z として表します。これは次の影響を受けると予想されます。

データ圧縮率 R: 直感的には、圧縮率が低いデータセットは情報密度が高いことを示します。

トレーニング損失 L: モデルがデータを記憶するのが難しいかどうかを示します。同じ基本モデルの下で、高いトレーニング損失が発生するのは、通常、データセット内のノイズや一貫性のない情報の存在が原因です。

• データの一貫性 C: データの一貫性は、前の状況を考慮した次のトークンの確率のエントロピーによって反映されます。通常、データの一貫性が高いほど、トレーニング損失が少なくなります。
• 平均データ品質 Q: データのサンプルレベルの平均品質を反映しており、さまざまな客観的および主観的な側面を通じて測定できます。
• 一定量のトレーニング データが与えられると、モデルのパフォーマンスは上記の要素によって推定できます。

ここで、f は暗黙の関数です。特定の基本モデルが与えられると、L のスケールは通常 R と C に依存し、次のように表すことができます:

均一性が高い、またはデータの一貫性が高いデータセットはモデルによって学習されやすいため、L は次のように表されます。 R と C では単調であると予想されます。したがって、上記の式は次のように書き換えることができます:

ここで、g' は逆関数です。上記の 3 つの方程式を組み合わせると、次のようになります:

ここで、 h は別の暗黙的な関数です。データ選択方法によって平均データ品質 Q が大きく変化しない場合は、変数 Q をほぼ定数として扱うことができます。したがって、最終的なパフォーマンスは次のように大まかに表すことができます:

これは、モデルのパフォーマンスがデータ圧縮率とトレーニング損失に関連していることを意味します。この関係をエントロピーの法則と呼びます。

エントロピーの法則に基づいて、次の 2 つの推論を提案します:

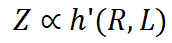
• C が定数とみなされる場合、トレーニング損失は圧縮率によって直接影響されます。したがって、モデルのパフォーマンスは圧縮率によって制御されます。データ圧縮率 R が高い場合、通常は Z の方が悪くなります。これは実験で検証されます。
• 同じ圧縮率の下では、トレーニング損失が高くなると、データの一貫性が低くなります。したがって、モデルによって学習される有効な知識はさらに限定される可能性があります。これを使用して、同様の圧縮率とサンプル品質を持つさまざまなデータに対する LLM のパフォーマンスを予測できます。この推論を実際に適用する方法については、後ほど説明します。

ZIP: 非常に軽量なデータ選択アルゴリズム

エントロピーの法則に基づいて、データ圧縮率を通じてデータサンプルを選択するデータ選択方法である ZIP を提案し、データの最大化を目指しました。限られたトレーニング データの予算内で有効な情報量を実現します。効率上の理由から、反復多段階貪欲パラダイムを採用して、比較的低い圧縮率で近似解を効率的に取得します。各反復では、最初にグローバル選択ステージを使用して圧縮率の低い候補サンプルのプールを選択し、情報密度の高いサンプルを見つけます。次に、粗粒度のローカル選択ステージを使用して、選択したサンプルとの冗長性が最も低い小さなサンプルのセットを選択します。最後に、追加するサンプル間の類似性を最小限に抑えるために、きめの細かいローカル選択ステージを使用します。上記のプロセスは、十分なデータが得られるまで継続されます。具体的なアルゴリズムは次のとおりです。

1. 異なる LLM および異なる LLM アライメント段階における ZIP 選択アルゴリズムの有効性

さまざまな SFT データ選択アルゴリズムを比較すると、ZIP 選択データに基づいてトレーニングされたモデルはパフォーマンスの面で利点があり、効率の面でも優れています。具体的な結果を以下の表に示します。

ZIP のモデルに依存しない、コンテンツに依存しない特性のおかげで、設定の調整段階でのデータ選択にも適用できます。 ZIP で選択されたデータにも大きな利点があります。具体的な結果を以下の表に示します。

2. エントロピーの法則の実験的検証

SFT データ選択実験に基づいて、モデル効果、データ圧縮率、および損失に基づいています。それぞれ、トレーニングの前のステップでのモデルの複数の関係曲線がフィッティングされました。結果を図 2 および 3 に示します。そこから、3 つの要因間の密接な相関関係が観察できます。まず、圧縮率の低いデータは通常、より良いモデルの結果につながります。これは、LLM の学習プロセスが情報圧縮に大きく関係しているため、圧縮率が低いデータはより多くのデータを意味します。知識が得られるため、コンプレッサーにとってより価値のあるものになります。同時に、圧縮率が低いほどトレーニング損失が大きくなることがわかります。これは、圧縮が難しいデータにはより多くの知識が含まれており、LLM がデータに含まれる知識を吸収することがより困難になるためです。

図 3 Llama-3-8B

実際のシナリオ アプリケーションにおける LLM トレーニング データの増分更新をガイドするエントロピー則を提供します。このタスク シナリオでは、トレーニング データの量は比較的安定しており、データのごく一部のみが変更されます。結果を図 4 に示します。ここで、 から ^{は段階的に更新される 5 つのデータ バージョンです。機密性の要件により、異なる圧縮率でのモデル効果の相対的な関係のみが示されています。エントロピーの法則の予測によれば、各増分更新後にデータ品質が大幅に低下しないと仮定すると、データ圧縮率が低下するにつれてモデルのパフォーマンスが向上することが期待できます。この予測は、図のデータ バージョン} から の結果と一致しています。ただし、データ バージョン

では損失とデータ圧縮率が異常に増加しており、トレーニング データの一貫性の低下によりモデルのパフォーマンスが低下する可能性があることを示しています。この予測は、その後のモデルの性能評価によってさらに確認されました。したがって、エントロピーの法則は、LLM トレーニングの指針として機能し、収束するまで完全なデータセットでモデルをトレーニングしなくても、LLM トレーニングの失敗の潜在的なリスクを予測できます。 LLM のトレーニングにかかる​​コストが高いことを考えると、これは特に重要です。

以上が中国科学技術大学とファーウェイ・ノアは、大規模モデルのパフォーマンス、データ圧縮率、トレーニング損失の関係を明らかにするためにエントロピー法則を提案しました。の詳細内容です。詳細については、PHP 中国語 Web サイトの他の関連記事を参照してください。