リーマン予想の大きな進歩!陶哲軒氏はMITとオックスフォードの新しい論文を強く推薦し、37歳のフィールズ賞受賞者も参加した
最近、ミレニアムの七大問題の一つとして知られるリーマン予想が新たな突破口を迎えました。
リーマン予想は数学における非常に重要な未解決の問題であり、素数の分布の正確な性質に関連しています (素数は 1 とそれ自体でしか割りることができない数であり、素数は次の点で基本的な役割を果たします)数論の役割)。
今日の数学文献には、リーマン予想 (またはその一般化された形式) の確立に基づいた数学的命題が 1,000 を超えています。言い換えれば、リーマン予想とその一般化された形式が証明されれば、これらの 1,000 を超える命題が定理として確立され、数学の分野に重大な影響を与えることになります。これらの命題の一部も有効性を失います。
新たな進歩は、MIT数学教授ラリー・ガスとオックスフォード大学数学研究所教授でフィールズ賞受賞者のジェームス・メイナードによる論文から生まれました。この論文を推薦した数学者のテレンス・タオ氏は、これらの論文は、リーマンのゼータ関数の零点に拘束された古典的な 1940 年のインガム (より一般的には、さまざまなディリクレ級数の大きな値の制御) に初めて実質的な改善をもたらしたと述べました。 80 年以上前に誕生したインガム限界は、これまで改善がなかったため、数学者が解析的数論で多くのことを行うことを制限していました。

しかし、陶哲軒氏は、これは重要な進歩ではあるが、リーマン予想の完全な解決にはまだ程遠いので、合理的に見るべきだとも述べました。
リーマン予想とは何ですか?
リーマン予想またはリーマン予想は、1859年にドイツの数学者ベルンハルト・リーマンによって提案されました。この予想は素数の分布と密接に関連しており、その中心的な内容にはリーマン ゼータ関数の非自明なゼロが含まれます。 Bernhard Riemann、出典:facts.net/
 リーマン仮説の内容は、完全な基本的な数学では説明できません。ざっくり言うと、リーマンゼータ関数と呼ばれる複素変数関数(つまり、変数も関数値も複素領域の値をとり得る関数)の予想です。リーマン ゼータ関数は、他の多くの関数と同様に、いくつかの点で値がゼロになります。これらの点は、リーマン ゼータ関数のゼロ点と呼ばれます。これらのゼロの中には、リーマン ゼータ関数と呼ばれる特に重要な重要なゼロがいくつかあります。リーマン仮説が推測していることは、すべての非自明なゼロ点は「臨界線」と呼ばれる特別な直線上に分布しているということです(人気サイエンスライターのルー・チャンハイ氏のブログより引用)。
リーマン仮説の内容は、完全な基本的な数学では説明できません。ざっくり言うと、リーマンゼータ関数と呼ばれる複素変数関数(つまり、変数も関数値も複素領域の値をとり得る関数)の予想です。リーマン ゼータ関数は、他の多くの関数と同様に、いくつかの点で値がゼロになります。これらの点は、リーマン ゼータ関数のゼロ点と呼ばれます。これらのゼロの中には、リーマン ゼータ関数と呼ばれる特に重要な重要なゼロがいくつかあります。リーマン仮説が推測していることは、すべての非自明なゼロ点は「臨界線」と呼ばれる特別な直線上に分布しているということです(人気サイエンスライターのルー・チャンハイ氏のブログより引用)。
リーマン ξ 関数は次のように定義されます:
リーマン仮説では、ξ 関数のすべての非自明なゼロの実部は 1/2 であると考えられます。これは、ζ(s)=0 で s が自明ではないゼロ (つまり、s が負の偶数ではない) の場合、s の実数部は 1/2 である必要があることを意味します。 リーマン予想は、今日世界で最も重要かつ最も期待されている数学的問題です。この予想が正しければ、自然数間の素数の分布を正確に記述することができ、数論、複素解析、その他の数学分野を解く際に幅広い応用と影響を与えることになります。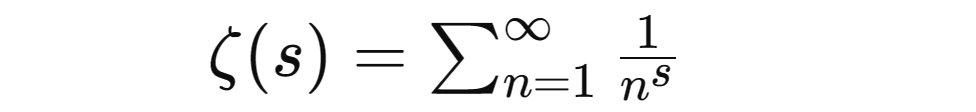 リーマン予想が提唱されてからこれまでに165年が経過しました。リーマン予想を証明しようとする研究は数多く行われてきましたが、どれも無駄に終わりました。
リーマン予想が提唱されてからこれまでに165年が経過しました。リーマン予想を証明しようとする研究は数多く行われてきましたが、どれも無駄に終わりました。
リーマン予想が提案されて以来、多くの数学者が証明を探求する旅を始めました。
1896 年、フランスの数学者ジャック アダマールとシャルル ジャン ド ラ ヴァレ プッサンは、直線上にゼロ点が存在しないことを独自に証明しました。リーマンが非自明なゼロに関して証明した他の特性と合わせて、これはすべての非自明なゼロが領域上に存在する必要があることを示しています。これは、素数定理の最初の完全な証明における重要なステップです。 1900 年、ドイツの数学者であり現代数学の父の一人であるデイヴィッド・ヒルベルトは、有名な 23 の質問にリーマン予想を含め、ゴールドバッハの仮説と合わせてヒルベルトのリスト第 8 問を作成しました。同時に、リーマン予想は、クレイ数学研究所のミレニアム賞に含まれる唯一のヒルベルト問題でもあります。
1914年、英国の数学者ゴッドフリー・ハロルド・ハーディは、直線上に無限のゼロ点が存在することを証明しました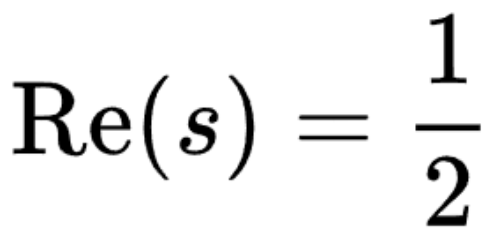 。その後、1921 年にハーディとイギリスの数学者ジョン アンサー リトルウッド、1942 年にセルバーグの研究 (臨界線定理) は、臨界線
。その後、1921 年にハーディとイギリスの数学者ジョン アンサー リトルウッド、1942 年にセルバーグの研究 (臨界線定理) は、臨界線  上のゼロ点の平均密度を計算することでした。
上のゼロ点の平均密度を計算することでした。
近年まで、リーマン予想を証明する試みはしばしば物議を醸していました。
2018年9月、ハイデルベルクでの前例のない演説が数学界に衝撃を与えました、89歳のアティヤ卿のリーマン予想の証明は世界的な注目を集めました。スポットライトを浴びながら、アティヤ卿は 45 分を費やして、150 年以上の歴史を持つこの数学的予想の証明を世界に発表しました。
しかし、アティヤ卿の証明は PPT の次のページだけです。そのような証明は説得力がないと思われます。リーマン予想を解決したかどうか尋ねられたとき、彼はこう答えた、「それはあなたの論理次第です。あなたが矛盾による証明を受け入れない種類の数学者でない限り、私は元のリーマン予想を証明しました。」 彼はまた、自分の証明を付け加えた。すべての問題を解決したわけではありませんし、今後も多くの問題が生じるでしょう。彼は最初の一歩を踏み出しただけです(最初の一歩が解決策です)。
残念なことに、アティヤ卿は 2019 年 1 月に亡くなりました。

さて、リーマン予想に異議を唱えた人がいます。
ガスとメイナードがしたこと
ガスとメイナードの新たな進歩について、有名な数学者テレサ・タオは次のようにコメントしました。数学の問題はまだ長い道のりです。」

論文リンク: https://arxiv.org/pdf/2405.20552
この研究が初めてであることを Tao Zhexuan のツイートから知りました。数学者のアルバート・インガムは、リーマンのゼータ関数の古典的な限界 (より一般的には、さまざまなディリクレ級数を支配する大きな値) において、1940 年頃に大幅な改善が行われました。
1940 年、数学者のアルバート インガムは、これらのゼロ点を記述する境界を提案しました。これは、当時の理論研究の基礎を形成しました。しかし、ガスとメイナードの研究まで、この境界はほとんど洗練されていませんでした。ガスとメイナードの研究は、インガムのこの限界を改善しただけでなく、彼らの方法は、多くの数論や解析問題において重要なディリクレ級数の大きな値を扱うための新しいツールと視点を提供しました。
この論文は、ディリクレ多項式の大きな値の頻度に関する新しい限界を証明します。これにより、長さ N のディリクレ多項式の推定値が改善され、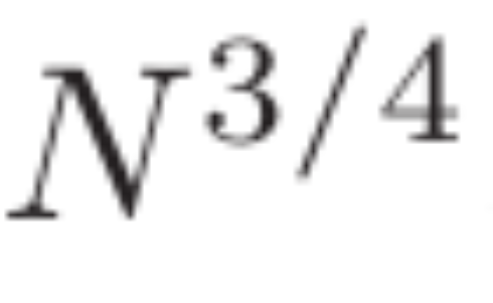 に近い値が得られます。さらに、この研究では、ゼロ点密度推定
に近い値が得られます。さらに、この研究では、ゼロ点密度推定 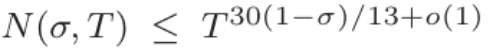 と、長さの短い間隔
と、長さの短い間隔 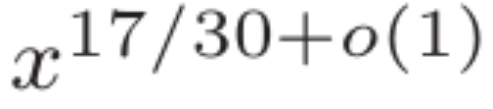 にわたる素数の漸近式を導出しています。
にわたる素数の漸近式を導出しています。
Tao Zhexuan 自身がこの研究について数学的な観点からいくつかの説明をしました。 ?(σ,?) がリーマン ζ 関数のゼロの数を表すものとします。ここで、実数部は少なくとも σ、虚数部は最大 T です。リーマン予想は、σ>1/2 であれば N (σ,?) が消滅することを示していますが、この仮説はまだ証明できません。しかし、次善の選択肢として、数学者は ?(σ,?) の自明ではない上限であるゼロ点密度推定を証明できます。
σ=3/4が重要な値であることが分かりました。 1940 年に、インガムは結合 ?(3/4,?)≪?(3/5+?(1)) を導き出しました。
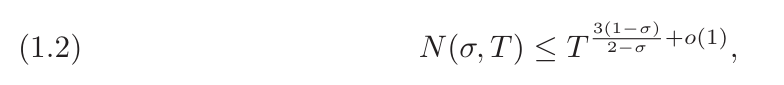
その後 80 年間にわたり、この境界に対する改善は、?(1) エラーのわずかな改良にすぎませんでした。このため、研究者は解析的数論でより詳細な研究を行うことが制限されています。たとえば、形式 (?,?+?^?) のほぼすべての短い区間で優れた素数定理を取得するために、人々は長い間制限されてきました。 ?>1/6 範囲までの場合、主な障害は、インガム境界が改善されていないことです。

ガスとメイナードは最終的にインガム境界を 3/5=0.6 から 13/25=0.52 に改善しました。これにより、解析的整数論にも多くの対応する改善がもたらされました。たとえば、研究者は、θ>1/6=0.166…からθ>2/15=0.133…までのほぼすべての短い区間で素数定理の範囲を証明できるようになりました。

著者について
ラリー・ガスは、2019 年 7 月から MIT で数学のクロード E. シャノン教授を務めており、2021 年に MacVicar フェローに選出されました。 彼は、Tom Mrowka の監督のもと、2005 年に MIT から博士号を取得しました。その後、スタンフォード大学の博士研究員、トロント大学の準教員職を経て、2011 年にクーラント研究所の教授に任命されました。その後、2012 年に教授として MIT 数学学部に加わりました。 Guth の研究対象は、計量幾何学、調和解析、および極値の組み合わせです。メートル幾何学とは、長さ、面積、体積を含む不等式の研究を指します。主な例としては、等周不等式や収縮不等式などがあります。ガスの研究の焦点は収縮不等式であり、もう 1 つの焦点は幾何学的不等式とトポロジーの間の関係を見つけることでした。 最近、Guth は調和解析と組み合わせ論の研究に取り組んでいます。多くの研究は、ユークリッド幾何学の未解決問題であるカケヤ問題、フーリエ解析における制限型推定、および極端な組み合わせ論における線出現率の推定に関連しています。 1987年生まれ。イギリスの数学者で、解析的整数論、特に素数論を研究分野としています。 数論における最も有名な問題のいくつかは、素数の分布に関連しています。素数の大規模分布は数論の定理 (より正確にはリーマン予想) に従っていますが、多くの自然問題は短い (または疎な) スケールを扱う必要があります。 ジェームズ・メイナードは2013年に双子素数予想に関して重要な結果を達成しました。彼は、間隔が 600 未満の素数のペアが無限に存在することを証明しました。この結果は、Zhang Yitang の 7,000 万間隔よりも小さいですが、彼の論文は Zhang Yitang より半年遅れて発表されましたが、彼の結果は数論の専門家の間で高く評価されました。
ジェームズ・メイナードは2013年に双子素数予想に関して重要な結果を達成しました。彼は、間隔が 600 未満の素数のペアが無限に存在することを証明しました。この結果は、Zhang Yitang の 7,000 万間隔よりも小さいですが、彼の論文は Zhang Yitang より半年遅れて発表されましたが、彼の結果は数論の専門家の間で高く評価されました。
Tao Zhexuan 氏は次のようにコメントしました。「正直に言うと、彼の表現方法は私のものよりもすっきりしています...彼の表現の方がわずかに強いことがわかりました。メイナードの手法は、衝撃的な方法でエレガントかつ強力です。」スクリーニング理論の限界を突破します。そして、一見反対の方向に、彼は素数が平均よりもはるかにまばらである場合があることを示しました。これは有名なエルデシュの問題ですが、何十年も実質的な進歩はありませんでした。
メイナードはまた、ディオファントス近似の分野で基礎的な研究を行い、モントリオール大学の数学教授コウコウロプロスとともにダフィン・シェーファー予想を解きました。 1941 年に提案されたこの予想は、典型的な実数を有理数で近似する方法を説明するヒンチンの定理の最終的な一般化と考えることができます。 2022 年、メイナードは解析的数論への貢献によりフィールズ賞を受賞しました。フィールズ賞は数学界で最も名誉ある賞であり、しばしば数学のノーベル賞とみなされます。ジェームズ メイナードは、素数の構造とディオファントス近似の理解に大きな進歩をもたらした解析的整数論への貢献を讃えられました。
2023 年に、彼は数学で再び New Horizons Award を受賞しました。
二人の数学者がリーマン予想などの世界の問題に関してさらに進歩することを楽しみにしています。 参考リンク: https://www.jiqizhixin.com/articles/2019-01-12
https://www.zhihu.com/tardis/zm/ art/557594612
https://news.mit.edu/2014/profile-larry-guth-0527 https://mathstodon.xyz/@tao/112557248794707738 https://zh.wikipedia.org/wiki/% E9% BB%8E% EBC%9% EBC%8% 9C% E6%83%B3
以上がリーマン予想の大きな進歩!陶哲軒氏はMITとオックスフォードの新しい論文を強く推薦し、37歳のフィールズ賞受賞者も参加したの詳細内容です。詳細については、PHP 中国語 Web サイトの他の関連記事を参照してください。

ホットAIツール

Undresser.AI Undress
リアルなヌード写真を作成する AI 搭載アプリ

AI Clothes Remover
写真から衣服を削除するオンライン AI ツール。

Undress AI Tool
脱衣画像を無料で

Clothoff.io
AI衣類リムーバー

Video Face Swap
完全無料の AI 顔交換ツールを使用して、あらゆるビデオの顔を簡単に交換できます。

人気の記事

ホットツール

メモ帳++7.3.1
使いやすく無料のコードエディター

SublimeText3 中国語版
中国語版、とても使いやすい

ゼンドスタジオ 13.0.1
強力な PHP 統合開発環境

ドリームウィーバー CS6
ビジュアル Web 開発ツール

SublimeText3 Mac版
神レベルのコード編集ソフト(SublimeText3)

ホットトピック
 7909
7909
 15
15
 1652
1652
 14
14
 1411
1411
 52
52
 1303
1303
 25
25
 1248
1248
 29
29
 ControlNet の作者がまたヒット作を出しました!写真から絵画を生成し、2 日間で 1.4,000 個のスターを獲得する全プロセス
Jul 17, 2024 am 01:56 AM
ControlNet の作者がまたヒット作を出しました!写真から絵画を生成し、2 日間で 1.4,000 個のスターを獲得する全プロセス
Jul 17, 2024 am 01:56 AM
これも Tusheng のビデオですが、PaintsUndo は別の道を歩んでいます。 ControlNet 作者 LvminZhang が再び生き始めました!今回は絵画の分野を目指します。新しいプロジェクト PaintsUndo は、開始されて間もなく 1.4kstar を獲得しました (まだ異常なほど上昇しています)。プロジェクトアドレス: https://github.com/lllyasviel/Paints-UNDO このプロジェクトを通じて、ユーザーが静止画像を入力すると、PaintsUndo が線画から完成品までのペイントプロセス全体のビデオを自動的に生成するのに役立ちます。 。描画プロセス中の線の変化は驚くべきもので、最終的なビデオ結果は元の画像と非常によく似ています。完成した描画を見てみましょう。
 オープンソース AI ソフトウェア エンジニアのリストのトップに立つ UIUC のエージェントレス ソリューションは、SWE ベンチの実際のプログラミングの問題を簡単に解決します
Jul 17, 2024 pm 10:02 PM
オープンソース AI ソフトウェア エンジニアのリストのトップに立つ UIUC のエージェントレス ソリューションは、SWE ベンチの実際のプログラミングの問題を簡単に解決します
Jul 17, 2024 pm 10:02 PM
AIxivコラムは、当サイトが学術的・技術的な内容を掲載するコラムです。過去数年間で、このサイトの AIxiv コラムには 2,000 件を超えるレポートが寄せられ、世界中の主要な大学や企業のトップ研究室がカバーされ、学術交流と普及を効果的に促進しています。共有したい優れた作品がある場合は、お気軽に寄稿するか、報告のために当社までご連絡ください。提出電子メール: liyazhou@jiqizhixin.com; zhaoyunfeng@jiqizhixin.com この論文の著者は全員、イリノイ大学アーバナ シャンペーン校 (UIUC) の Zhang Lingming 教師のチームのメンバーです。博士課程4年、研究者
 RLHF から DPO、TDPO に至るまで、大規模なモデル アライメント アルゴリズムはすでに「トークンレベル」になっています
Jun 24, 2024 pm 03:04 PM
RLHF から DPO、TDPO に至るまで、大規模なモデル アライメント アルゴリズムはすでに「トークンレベル」になっています
Jun 24, 2024 pm 03:04 PM
AIxivコラムは、当サイトが学術的・技術的な内容を掲載するコラムです。過去数年間で、このサイトの AIxiv コラムには 2,000 件を超えるレポートが寄せられ、世界中の主要な大学や企業のトップ研究室がカバーされ、学術交流と普及を効果的に促進しています。共有したい優れた作品がある場合は、お気軽に寄稿するか、報告のために当社までご連絡ください。提出メール: liyazhou@jiqizhixin.com; zhaoyunfeng@jiqizhixin.com 人工知能の開発プロセスにおいて、大規模言語モデル (LLM) の制御とガイダンスは常に中心的な課題の 1 つであり、これらのモデルが両方とも確実に機能することを目指しています。強力かつ安全に人類社会に貢献します。初期の取り組みは人間のフィードバックによる強化学習手法に焦点を当てていました (RL
 OpenAI Super Alignment チームの遺作: 2 つの大きなモデルがゲームをプレイし、出力がより理解しやすくなる
Jul 19, 2024 am 01:29 AM
OpenAI Super Alignment チームの遺作: 2 つの大きなモデルがゲームをプレイし、出力がより理解しやすくなる
Jul 19, 2024 am 01:29 AM
AIモデルによって与えられた答えがまったく理解できない場合、あなたはそれをあえて使用しますか?機械学習システムがより重要な分野で使用されるにつれて、なぜその出力を信頼できるのか、またどのような場合に信頼してはいけないのかを実証することがますます重要になっています。複雑なシステムの出力に対する信頼を得る方法の 1 つは、人間または他の信頼できるシステムが読み取れる、つまり、考えられるエラーが発生する可能性がある点まで完全に理解できる、その出力の解釈を生成することをシステムに要求することです。見つかった。たとえば、司法制度に対する信頼を築くために、裁判所に対し、決定を説明し裏付ける明確で読みやすい書面による意見を提供することを求めています。大規模な言語モデルの場合も、同様のアプローチを採用できます。ただし、このアプローチを採用する場合は、言語モデルが
 arXiv 論文は「弾幕」として投稿可能、スタンフォード alphaXiv ディスカッション プラットフォームはオンライン、LeCun は気に入っています
Aug 01, 2024 pm 05:18 PM
arXiv 論文は「弾幕」として投稿可能、スタンフォード alphaXiv ディスカッション プラットフォームはオンライン、LeCun は気に入っています
Aug 01, 2024 pm 05:18 PM
乾杯!紙面でのディスカッションが言葉だけになると、どんな感じになるでしょうか?最近、スタンフォード大学の学生が、arXiv 論文のオープン ディスカッション フォーラムである alphaXiv を作成しました。このフォーラムでは、arXiv 論文に直接質問やコメントを投稿できます。 Web サイトのリンク: https://alphaxiv.org/ 実際、URL の arXiv を alphaXiv に変更するだけで、alphaXiv フォーラムの対応する論文を直接開くことができます。この Web サイトにアクセスする必要はありません。その中の段落を正確に見つけることができます。論文、文: 右側のディスカッション エリアでは、ユーザーは論文のアイデアや詳細について著者に尋ねる質問を投稿できます。たとえば、次のような論文の内容についてコメントすることもできます。
 リーマン予想の大きな進歩!陶哲軒氏はMITとオックスフォードの新しい論文を強く推薦し、37歳のフィールズ賞受賞者も参加した
Aug 05, 2024 pm 03:32 PM
リーマン予想の大きな進歩!陶哲軒氏はMITとオックスフォードの新しい論文を強く推薦し、37歳のフィールズ賞受賞者も参加した
Aug 05, 2024 pm 03:32 PM
最近、2000年代の7大問題の一つとして知られるリーマン予想が新たなブレークスルーを達成した。リーマン予想は、数学における非常に重要な未解決の問題であり、素数の分布の正確な性質に関連しています (素数とは、1 とそれ自身でのみ割り切れる数であり、整数論において基本的な役割を果たします)。今日の数学文献には、リーマン予想 (またはその一般化された形式) の確立に基づいた 1,000 を超える数学的命題があります。言い換えれば、リーマン予想とその一般化された形式が証明されれば、これらの 1,000 を超える命題が定理として確立され、数学の分野に重大な影響を与えることになります。これらの命題の一部も有効性を失います。 MIT数学教授ラリー・ガスとオックスフォード大学から新たな進歩がもたらされる
 最初の Mamba ベースの MLLM が登場しました!モデルの重み、トレーニング コードなどはすべてオープンソースです
Jul 17, 2024 am 02:46 AM
最初の Mamba ベースの MLLM が登場しました!モデルの重み、トレーニング コードなどはすべてオープンソースです
Jul 17, 2024 am 02:46 AM
AIxivコラムは、当サイトが学術的・技術的な内容を掲載するコラムです。過去数年間で、このサイトの AIxiv コラムには 2,000 件を超えるレポートが寄せられ、世界中の主要な大学や企業のトップ研究室がカバーされ、学術交流と普及を効果的に促進しています。共有したい優れた作品がある場合は、お気軽に寄稿するか、報告のために当社までご連絡ください。提出電子メール: liyazhou@jiqizhixin.com; zhaoyunfeng@jiqizhixin.com。はじめに 近年、さまざまな分野でマルチモーダル大規模言語モデル (MLLM) の適用が目覚ましい成功を収めています。ただし、多くの下流タスクの基本モデルとして、現在の MLLM はよく知られた Transformer ネットワークで構成されています。
 公理的トレーニングにより、LLM は因果推論を学習できます。6,700 万個のパラメータ モデルは、1 兆個のパラメータ レベル GPT-4 に匹敵します。
Jul 17, 2024 am 10:14 AM
公理的トレーニングにより、LLM は因果推論を学習できます。6,700 万個のパラメータ モデルは、1 兆個のパラメータ レベル GPT-4 に匹敵します。
Jul 17, 2024 am 10:14 AM
LLM に因果連鎖を示すと、LLM は公理を学習します。 AI はすでに数学者や科学者の研究を支援しています。たとえば、有名な数学者のテレンス タオは、GPT などの AI ツールを活用した研究や探索の経験を繰り返し共有しています。 AI がこれらの分野で競争するには、強力で信頼性の高い因果推論能力が不可欠です。この記事で紹介する研究では、小さなグラフでの因果的推移性公理の実証でトレーニングされた Transformer モデルが、大きなグラフでの推移性公理に一般化できることがわかりました。言い換えれば、Transformer が単純な因果推論の実行を学習すると、より複雑な因果推論に使用できる可能性があります。チームが提案した公理的トレーニング フレームワークは、デモンストレーションのみで受動的データに基づいて因果推論を学習するための新しいパラダイムです。




