
私が Python を学習していたとき、先生は私たちにフィボナッチ数列の N 番目の数を計算するという宿題を出しました。
とても簡単だと思うので、次のコードを書きます:
def fib(n):
if n == 0:
return 0
elif n == 1:
return 1
else:
return fib(n - 1) + fib(n - 2)
後から、この種の解決策には時間がかかりすぎることが分かりました。
解法を反復に変更します。
def fib(n):
ls = [1,1]
for i in range(2,n):
ls.append(ls[i-1]+ls[i-2])
return ls[n-1]
私は matplotlib を使用して、それにかかる時間を描画します:
import time
import matplotlib.pyplot as plt
def bench_mark(func, *args):
# calculate the time
start = time.perf_counter()
result = func(*args)
end = time.perf_counter()
return end - start, result # return the time and the result
def fib(n):
ls = [1,1]
for i in range(2,n):
ls.append(ls[i-1]+ls[i-2])
return ls[n-1]
mark_list = []
for i in range(1,10000):
mark = bench_mark(fib,i)
mark_list.append(mark[0])
print(f"size : {i} , time : {mark[0]}")
plt.plot(range(1, 10000), mark_list)
plt.xlabel('Input Size')
plt.ylabel('Execution Time (seconds)')
plt.title('Test fot fibonacci')
plt.grid(True)
plt.show()
結果は次のとおりです:
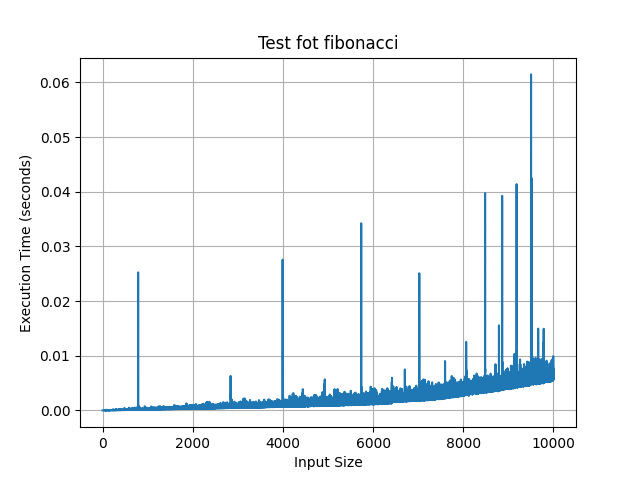
かかる時間は非常に短いです。
しかし、私は fib(300000) を書きます、コストは 5.719049899998936 秒です。長すぎます。
大人になると CACHE を学ぶので、結果を保存するために dict を使用するようにソリューションを変更します。
from functools import lru_cache
@lru_cache(maxsize=None)
def fib(n):
if n < 2:
return 1
else:
return fib(n - 1) + fib(n - 2)
または、自分で CACHE を作成することもできます。
def fib(n, cache={}):
if n in cache:
return cache[n]
elif n < 2:
return 1
else:
ls = [1, 1]
for i in range(2, n):
next_value = ls[-1] + ls[-2]
ls.append(next_value)
cache[i] = next_value
cache[n-1] = ls[-1]
return ls[-1]
以上がフィボナッチ数列を計算するプログラムをどこまで最適化できるでしょうか?の詳細内容です。詳細については、PHP 中国語 Web サイトの他の関連記事を参照してください。