Java での再帰

Java における再帰とは、「メソッドが直接的または間接的にそれ自体 (同じメソッド) を連続的に呼び出すこと」と定義されています。再帰関数は、結果が得られるまで同じ一連の操作を何度も実行する必要がある状況で使用されます。何度か反復を実行し、反復するたびに問題ステートメントが単純になっていきます。 Java の再帰は、同じ問題のより小さなブロックの解に基づいて問題を解決する方法です。無限の可能性のある反復のほとんどは再帰によって解決できます。再帰はステートメントをループする代替方法であると言えます。再帰関数を適切に使用しなかった場合、無限回実行されます。

構文:

広告 このカテゴリーの人気コース JAVA マスタリー - スペシャライゼーション | 78 コース シリーズ | 15 回の模擬テスト

returntype methodName()
{
//logic for application
methodName();//recursive call
}

Java で無限再帰条件を阻止するにはどうすればよいですか?

無限条件を停止するには、次のものが必要です:

• 基本条件: 条件が再帰関数を停止するかどうかを内部で指定します。
• 再帰呼び出し: 適切な再帰呼び出し。

再帰関数は 2 つの方法で呼び出すことができます:

1.直接再帰呼び出し

メソッド本体内から同じメソッドを呼び出した場合。

構文:

returntype methodName()
{
//logic for application
methodName();//recursive call
}

例:

数値の階乗は直接再帰の例です。再帰の基本原理は、複雑な問題をより小さな問題に分割することで解決することです。たとえば、数値の階乗の場合、「i-1」の階乗がわかっていれば、「i」の階乗を計算します。

コード:

public class Factorial {
static int fact(int i){
if (i == 1)
return 1;
else
return(i * fact(i-1));
}
public static void main(String[] args) {
System.out.println("The factorial of given number 6 is: "+fact(6));
}
}

出力:

2.間接/相互再帰呼び出し

別のメソッドからメソッドを呼び出し、最初のメソッドから別のメソッドを呼び出した場合は、その逆になります。

構文:

<firstIndirectRecursive()
{
// Logic
secondIndirectRecursive();
}
secondIndirectRecursive()
{
//Logic
firstIndirectRecursive();
}

例:

間接再帰を示すために、指定された入力から指定された数値が偶数か奇数かを調べるために使用される次のプログラムを使用します。

コード:

import java.util.Scanner;
public class IndirectRecursion {
public static boolean oddNum(int i) {
if (i<0) throw new IllegalArgumentException("Number is negative");
if(i == 0){
return false;
} else {
return evenNum(i-1);
}
}
public static boolean evenNum(int i) {
if (i<0) throw new IllegalArgumentException("Number is negative");
if(i == 0){
return true;
} else {
return oddNum(i-1);
}
}
public static void main(String[] args) {
Scanner inputNum = new Scanner(System.in);
System.out.print("Give a number: ");
int n = inputNum.nextInt();
if (evenNum(n)) System.out.println(n + " is even");
else System.out.println(n + " is odd");
inputNum.close();
}
}

出力:

Java での再帰の例

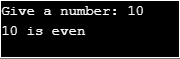
ここでは、再帰法を使用して問題を解決するための例をいくつか示します。

例 #1 – フィボナッチ数列

number3=number1+number2 の場合、「n」個の数値のセットはフィボナッチ数列にあると言われます。つまり、各数値がその前の 2 つの数値の合計です。したがって、シーケンスは常に 0 と 1 のような最初の 2 桁で始まります。3 桁目は 0 と 1 の合計で 1 になり、4 番目の数字は 1 と 1 の加算で 2 となり、シーケンスは続きます。

フィボナッチ数列を生成するには、Java で次のコードを確認してください:

コード:

public class FibonacciSeries{
static int num1=0,num2=1,num3=0;
static void fibonacci(int n){
if(n>0){
num3 = num1 + num2;
num1 = num2;
num2 = num3;
System.out.print(" "+num3);
fibonacci(n-1);
}
}
public static void main(String args[]){
int n=10;
System.out.print(num1+" "+num2);//printing constant first two digits 0 and 1
fibonacci(n-2);//Since first two numbers are already done
}
}

出力:

ここでは、最初の 2 つの数値が 0 と 1 に初期化されて出力されます。変数「num1」、「num2」、および「num3」は、必要なシーケンスを生成するために使用されます。変数「num3」は「num1」と「num2」を加算したもので、コードのようにシャッフルすることで数値を1つ左にシフトします。ここでは関数「フィボナッチ」が再帰的に呼び出され、反復ごとに「n」の値が 1 ずつ減ります。したがって、「n」が値 0 に達するとすぐに再帰は終了します。

例 #2 – ハノイの塔

これは古典的な数学の問題で、3 つの極とサイズの異なる「n」個の円盤があります。パズルは次のようになります:

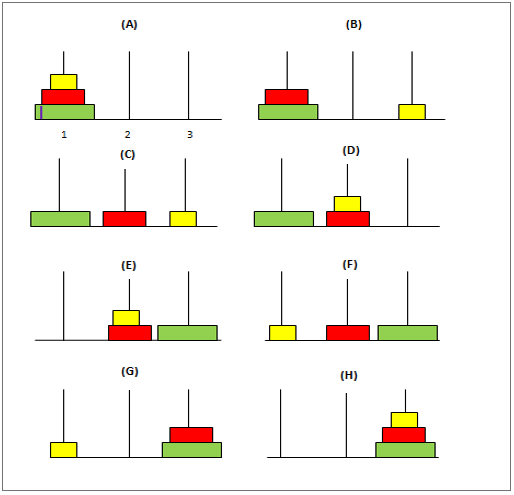
最初に、最初のポールには、最大のディスクがポールの下部に、最小のディスクがポールの上部に配置されるようにディスクが配置されます。目的は、これらのディスクを最初の極と同じ位置に保ちながら、最初の極から 3 番目の極まで移動することです。これらのディスクを移動する際に留意すべきいくつかの条件を次に示します。

• 一度に移動する必要があるディスクは 1 つだけです。
• このプロセスでは、小さなディスクの上に大きなディスクを配置することは許可されません。
• 2 番目 (中央) のポールは、ディスクを最初のポールから 2 番目のポールに移動する際の仲介に使用できます。

以下は、パズルを解くために使用できる Java コードです:

コード:

public class TowerOfHanoi {
public static void main(String[] args) {
int count = 3;
tower(count, 'A', 'B', 'C');
}
public static void tower(int first, char disk1, char temp, char disk2) {
if (first == 1) {
System.out.println("Disk 1 from " + disk1 + " to " + disk2);
} else {
tower(first - 1, disk1, disk2, temp);
System.out.println("Disk " + first + " from " + disk1 + " to " + disk2);
tower(first - 1, temp, disk1, disk2);
}
}
}

出力:

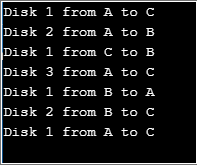
Here the variable “count” represents the number of discs to be used. The function “tower” is the recursive function used to move the discs from rod 1 to rod 3. A simple solution to this problem can be provided by considering 2 discs at first.

• First, we start by moving disc1 from rod 1 to rod 2.
• Next, we move disc2 to rod 3.
• Finally, we finish by moving disc1 to rod 3, completing the required solution.

This same principle is applied for the “n” number of discs by moving (n-1)the disc from rod 1 to 2 and following similar steps as above.

Example #3 – Factorial of Number

Code:

package com.recursion;
import java.util.Scanner;
public class FactorialOfNumber {
public static void main(String[] args) {
Scanner scanner = new Scanner(System.in);
System.out.println("Which number factorial do you want?=>");
//taking input from the user
int input = scanner.nextInt();
System.out.println("Factorial of " + input + "! is=>"+getMyFactorialNumber(input));
scanner.close();
}
public static long getMyFactorialNumber(int inputNumber) {
if (inputNumber == 1)//base condition
return 1;
return inputNumber * getMyFactorialNumber(inputNumber - 1);//recursive call
}
}

Output:

Example #4 – Armstrong Number

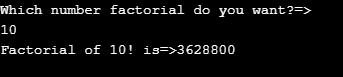
Code:

import java.util.Scanner;
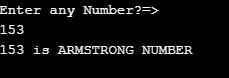
//ARMSTRONG number means sum of numbers of cubes equal to the number
public class ArmstrongNumber {
public static void main(String[] args) {
Scanner scanner = new Scanner(System.in);
System.out.println("Enter any Number?=>");
// taking input from the user
int input = scanner.nextInt();
//calling isArmstrongNumber() method and put in a variable
double checkNumber=isArmstrongNumber(input);
//checking the number
if(input==checkNumber)
{
System.out.println(input+" is ARMSTRONG NUMBER");
}
else
{
System.out.println(input+" not is ARMSTRONG NUMBER");
}
scanner.close();
}
static int remainderNumber;
static double total = 0;
public static double isArmstrongNumber(int inputNumber) {
if (inputNumber > 0) {
remainderNumber = inputNumber % 10;//separating digits
total = total + Math.pow(remainderNumber, 3);//cubes sum
isArmstrongNumber(inputNumber / 10);//recursive call
}
return total;
}
}

Output:

Example #5 – Palindrome Number

Code:

import java.util.Scanner;
public class PalindromeNumber {
public static void main(String[] args) {
Scanner scanner = new Scanner(System.in);
System.out.println("Enter any Number=>");
// taking input from the user
int input = scanner.nextInt();
int checkNumber = palindromeNumberOrNot(input,0);
if (checkNumber == input)
{
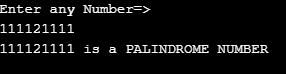
System.out.println(input+" is a PALINDROME NUMBER");
}
else
{
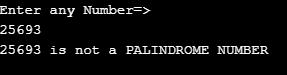
System.out.println(input+" is not a PALINDROME NUMBER");
}
scanner.close();
}
public static int palindromeNumberOrNot(int inputNumber,int baseNumber) {
if (inputNumber == 0)// base case
return baseNumber;
baseNumber = (baseNumber * 10) + (inputNumber % 10);// getting the reverse of the number and stores in temp
return palindromeNumberOrNot(inputNumber/10,baseNumber);//recursive call
}
}

Output:

Conclusion

Recursive functions are relatively simpler to code, but they are also not that efficient as compared to the other existing methods. Hence they are majorly used in cases where the time given for development is less and also where a significant pattern can be observed in the problem.

以上がJava での再帰の詳細内容です。詳細については、PHP 中国語 Web サイトの他の関連記事を参照してください。