np.einsumのパフォーマンスを調査する-Python チュートリアル-php.cn

私の前回のブログ投稿の読者が、スライスごとの matmul のような操作では、パラメーターリストで最適化フラグをオンにしない限り、np.einsum は np.matmul よりもかなり遅いと指摘しました。 np.einsum(.. .、最適化 = True).

少し懐疑的だったので、Jupyter ノートブックを起動して、いくつかの予備テストを行いました。そして、まったくそのとおりです。最適化によってまったく違いが生じるはずのない 2 つのオペランドの場合であってもです。

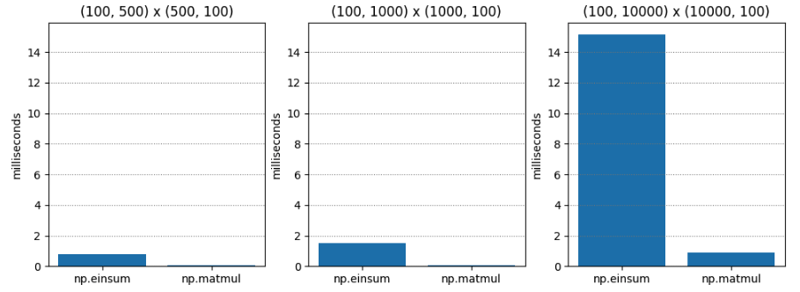
テスト 1 は非常に単純です。さまざまな次元の 2 つの C 次 (行主次数とも呼ばれる) 行列の行列乗算です。 np.matmul は一貫して約 20 倍高速です。

Investigating the performance of np.einsum

M1	M2	np.einsum	np.matmul	np.einsum / np.matmul
(100, 500)	(500, 100)	0.765	0.045	17.055
(100, 1000)	(1000, 100)	1.495	0.073	20.554
(100, 10000)	(10000, 100)	15.148	0.896	16.899

テスト 2 では、optimize=True を使用すると、結果は大幅に異なります。 np.einsum は依然として遅いですが、最悪の場合でも約 1.5 倍遅いだけです!

Investigating the performance of np.einsum

M1	M2	np.einsum	np.matmul	np.einsum / np.matmul
(100, 500)	(500, 100)	0.063	0.043	1.474
(100, 1000)	(1000, 100)	0.086	0.067	1.284
(100, 10000)	(10000, 100)	1.000	0.936	1.068

なぜ？

最適化フラグについての私の理解は、オペランドが 3 つ以上ある場合に最適な短縮順序を決定するということです。ここでは、オペランドは 2 つだけです。つまり、最適化によって違いが生じるはずはありませんね?

しかし、optimize は単に縮小注文を選択する以上のことを行っているのではないでしょうか? おそらく最適化はメモリレイアウトを認識しており、これは行優先レイアウトと列優先レイアウトに関係があるのでしょうか?

小学生の行列乗算の方法では、単一のエントリを計算するために、op1 の行を反復処理し、op2 の列を反復処理するため、2 番目の引数を列優先の順序にすると速度が向上する可能性があります。 np.einsum の場合 (np.einsum は、小学生の行列乗算の内部メソッドの一般化バージョンのようなものだと仮定します。私はこれが真実だと思います)。

そこで、テスト 3 では、2 番目のオペランドに列優先行列を渡して、optimize=False の場合に np.einsum が高速化するかどうかを確認しました。

結果は次のとおりです。驚くべきことに、np.einsum は依然としてかなり悪化しています。明らかに、私には理解できない何かが起こっています。おそらく、最適化が True の場合、np.einsum はまったく異なるコードパスを使用しますか? 掘り始めましょう。

Investigating the performance of np.einsum

M1	M2	np.einsum	np.matmul	np.einsum / np.matmul
(100, 500)	(500, 100)	1.486	0.056	26.541
(100, 1000)	(1000, 100)	3.885	0.125	31.070
(100, 10000)	(10000, 100)	49.669	1.047	47.444

さらに深くなる

Numpy 1.12.0 のリリースノートには、最適化フラグの導入について言及されています。ただし、最適化の目的は、一連のオペランド内の引数が結合される順序 (つまり、結合性) を決定することのようです。つまり、最適化は 2 つのオペランドだけで違いを生むべきではないのですね。リリースノートは次のとおりです:

np.einsum は、縮小順序を最適化する optimize 引数をサポートするようになりました。たとえば、np.einsum は、N^4 のようにスケールするチェーンドットの例 np.einsum(‘ij,jk,kl->il’, a, b, c) を 1 回のパスで完了します。ただし、optimize=True の場合、np.einsum は中間配列を作成して、このスケーリングを N^3 または事実上 np.dot(a, b).dot(c) に削減します。スケーリングを減らすための中間テンソルの使用は、一般的な einsum 合計表記に適用されています。詳細については、np.einsum_path を参照してください。

謎をさらに複雑にするのは、その後のリリースノートの一部では、np.einsum が tensordot (適切な場合には BLAS 自体を使用する) を使用するようにアップグレードされたことを示しています。さて、それは有望に思えます。

しかし、最適化が True の場合、だけ高速化が見られるのはなぜでしょうか? 何が起こっているのですか?

numpy/numpy/_core/einsumfunc.py で def einsum(*operands, out=None, optimize=False, **kwargs) を読み取ると、ほぼすぐに次の早期アウトロジックにたどり着きます。

    # If no optimization, run pure einsum
    if optimize is False:
        if specified_out:
            kwargs['out'] = out
        return c_einsum(*operands, **kwargs)

ログイン後にコピー

c_einsum は tensordot を利用しますか? 私はそれを疑う。コードの後半で、1.14 ノートが参照していると思われる tensordot 呼び出しがわかります。

    # Start contraction loop
    for num, contraction in enumerate(contraction_list):

        ...

        # Call tensordot if still possible
        if blas:

            ...

            # Contract!
            new_view = tensordot(
                *tmp_operands, axes=(tuple(left_pos), tuple(right_pos))
            )

ログイン後にコピー

それでは、何が起こっているのかを説明します:

optimize が True の場合、たとえ 2 つのオペランドが単純な場合であっても、contraction_list ループが実行されます。
tensordot は、contraction_list ループでのみ呼び出されます。
したがって、最適化が True の場合は、tensordot (したがって BLAS) を呼び出します。

私にとって、これはバグのように思えます。私見では、np.einsum の先頭にある「早期アウト」は、オペランドが tensordot と互換性があるかどうかを検出し、可能であれば tensordot を呼び出す必要があります。そうすれば、最適化が False の場合でも、明らかな BLAS の高速化が得られます。結局のところ、最適化のセマンティクスは BLAS の使用法ではなく短縮順序に関係しており、これは当然のことだと思います。

ここでの利点は、tensordot 呼び出しと同等の操作のために np.einsum を呼び出す人が適切な速度向上を得ることができ、パフォーマンスの観点から np.einsum の危険性が少し低くなるということです。

c_einsum は実際にどのように機能するのでしょうか?

確認するために C コードを詳しく調べてみました。実装の核心はここにあります。

引数の解析とパラメータの準備を大量に行った後、軸の反復順序が決定され、専用の反復子が準備されます。反復子からの各利回りは、すべてのオペランドを同時にストライドするための異なる方法を表します。

    # If no optimization, run pure einsum
    if optimize is False:
        if specified_out:
            kwargs['out'] = out
        return c_einsum(*operands, **kwargs)

ログイン後にコピー

特定の特殊な場合の最適化が適用されないと仮定すると、関連するデータ型に基づいて適切な積和 (SOP) 関数が決定されます。

    # Start contraction loop
    for num, contraction in enumerate(contraction_list):

        ...

        # Call tensordot if still possible
        if blas:

            ...

            # Contract!
            new_view = tensordot(
                *tmp_operands, axes=(tuple(left_pos), tuple(right_pos))
            )

ログイン後にコピー

次に、次に示すように、この積和 (SOP) 演算はイテレータから返される各マルチオペランドストライドで呼び出されます。

    /* Allocate the iterator */
    iter = NpyIter_AdvancedNew(nop+1, op, iter_flags, order, casting, op_flags,
                               op_dtypes, ndim_iter, op_axes, NULL, 0);

ログイン後にコピー

これが einsum の仕組みについての私の理解ですが、確かにまだ少し薄いですが、私が費やした時間以上の価値があります。

しかし、これは、行列の乗算の小学生の方法を一般化したギガブレイン版のように機能するという私の疑念を裏付けています。最終的には、オペランドを移動する「ストライダー」に依存する一連の「積和」演算に委譲されます。これは、行列の乗算を学習するときに指で行うこととそれほど変わりません。