コーナーに到達するための最小限の障害物の除去

2290。コーナーに到達するための最小限の障害物の除去

難易度: 難しい

トピック: 配列、幅優先検索、グラフ、ヒープ (優先キュー)、行列、最短パス

サイズ m x n の 0 インデックス付き 2D 整数配列グリッドが与えられます。各セルには次の 2 つの値のいずれかが含まれます:

• 0 は 空の セル、
を表します。
• 1 は、除去できる障害物を表します。

空のセルから上下左右に移動できます。

障害物の最小数を返して削除し、左上隅 (0, 0) から右下隅に移動できるようにしますコーナー (m - 1, n - 1).

例 1:

• 入力: グリッド = [[0,1,1],[1,1,0],[1,1,0]]
• 出力: 2
• 説明: (0, 1) と (0, 2) にある障害物を除去して、(0, 0) から (2, 2) までのパスを作成できます。
  少なくとも 2 つの障害物を取り除く必要があることがわかり、2 を返します。
  2 つの障害物を除去してパスを作成する他の方法がある可能性があることに注意してください。

例 2:

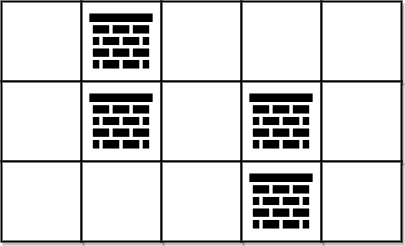
• 入力: グリッド = [[0,1,0,0,0],[0,1,0,1,0],[0,0,0,1,0]]
• 出力: 0
• 説明: 障害物を除去せずに (0, 0) から (2, 4) に移動できるため、0 を返します。

制約:

m == グリッドの長さ
n == グリッド[i].length
1 5 2 5 Grid[i][j] は 0 または 1 です。
グリッド[0][0] == グリッド[m - 1][n - 1] == 0

ヒント:

セルがノード、エッジが隣接するセルの間にあるグラフとしてグリッドをモデル化します。障害物のあるセルへのエッジのコストは 1 で、他のすべてのエッジのコストは 0 です。
0-1 幅優先検索またはダイクストラのアルゴリズムを使用していただけますか?

解決策:

グリッド内の各セルがノードであるグラフを使用して、この問題をモデル化する必要があります。目標は、削除する必要がある障害物 (1 秒) の数を最小限に抑えながら、左上隅 (0, 0) から右下隅 (m-1, n-1) までナビゲートすることです。

アプローチ：

1. グラフ表現:

   • グリッド内の各セルはノードです。
   • 隣接するセル間の移動 (上下左右) はエッジとして扱われます。
   • エッジが 1 (障害物) のセルを通過する場合、コストは 1 (障害物を取り除く)、0 (空のセル) を通過する場合、コストは 0 です。

2. アルゴリズムの選択:

   • 除去される障害物の数を最小限に抑える必要があるため、0-1 BFS (両端キューを使用した幅優先検索) または優先キューを備えた ダイクストラのアルゴリズム を使用できます。
   • 各エッジのコストが 0 または 1 であるため、0-1 BFS がここでは適しています。

3. 0-1 BFS:

   • デキュー (両端キュー) を使用して、さまざまなコストでノードを処理します。
     • コスト 0 のセルを両端キューの先頭にプッシュします。
     • コスト 1 のセルを両端キューの後ろにプッシュします。
   • そのアイデアは、グリッドを探索し、最初に障害物の除去を必要としないパスを常に拡張し、必要な場合にのみ障害物を除去することです。

このソリューションを PHP で実装してみましょう: 2290。コーナーに到達するための最小限の障害物の除去

<?php
/**
 * @param Integer[][] $grid
 * @return Integer
 */
function minimumObstacles($grid) {
    ...
    ...
    ...
    /**
     * go to ./solution.php
     */
}

// Test Case 1
$grid1 = [
    [0, 1, 1],
    [1, 1, 0],
    [1, 1, 0]
];
echo minimumObstacles($grid1) . PHP_EOL; // Output: 2

// Test Case 2
$grid2 = [
    [0, 1, 0, 0, 0],
    [0, 1, 0, 1, 0],
    [0, 0, 0, 1, 0]
];
echo minimumObstacles($grid2) . PHP_EOL; // Output: 0
?>

説明：

1. 入力解析:

   • グリッドは 2D 配列として取得されます。
   • 行と列は境界チェックのために計算されます。

2. デックの実装:

   • SplDoublyLinkedList は両端キューをシミュレートするために使用されます。前方 (シフト解除) または後方 (プッシュ) での要素の追加をサポートします。

3. 訪問済み配列:

   • 冗長な処理を避けるために、すでに訪問したセルを追跡します。

4. 0-1 BFS ロジック:

   • コスト 0 で (0, 0) から開始します。
   • 各隣接セルについて:
     • 空の場合 (grid[nx][ny] == 0)、同じコストで両端キューの先頭に追加します。
     • それが障害物 (grid[nx][ny] == 1) である場合は、増加したコストで両端キューの後ろに追加します。

5. 結果を返す:

   • 右下隅に到達したら、コストを返します。
   • 有効なパスが存在しない場合 (問題により有効なパスが存在することが保証されています)、-1 を返します。

---

複雑：

• 時間計算量: O(m x n)、m は行数、n は列の数です。各セルは 1 回処理されます。
• 空間複雑度: O(m x n)、訪問された配列と両端キューの場合。

この実装は、指定された制約内で効率的に動作します。

連絡先リンク

このシリーズが役立つと思われた場合は、GitHub で リポジトリ にスターを付けるか、お気に入りのソーシャル ネットワークで投稿を共有することを検討してください。あなたのサポートは私にとって大きな意味を持ちます!

このような役立つコンテンツがさらに必要な場合は、お気軽にフォローしてください:

• LinkedIn
• GitHub

以上がコーナーに到達するための最小限の障害物の除去の詳細内容です。詳細については、PHP 中国語 Web サイトの他の関連記事を参照してください。